27.3位似(2)
图片预览

文档简介
(共12张PPT)
如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形, 这个点P叫做位似中心, 这时的相似比又称为位似比.
1.什么叫位似图形
2.位似图形的性质
位似图形上的任意一对对应点到位似中心的距离之比等于位似比
3.利用位似可以把一个图形放大或缩小
D
E
F
A
O
B
C
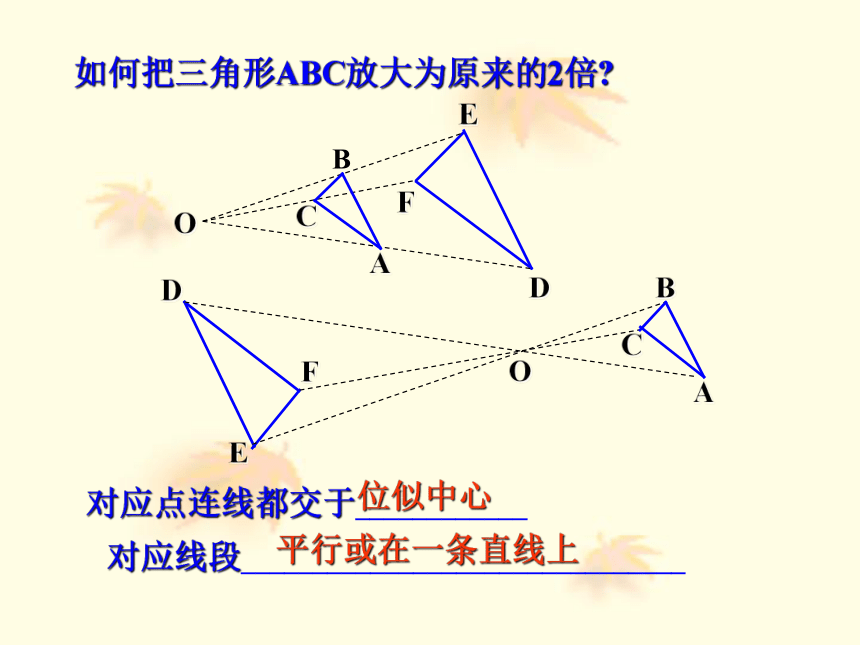
如何把三角形ABC放大为原来的2倍
D
E
F
A
O
B
C
对应点连线都交于____________
对应线段_______________________________
位似中心
平行或在一条直线上
B'
A'
x
y
B
A
o
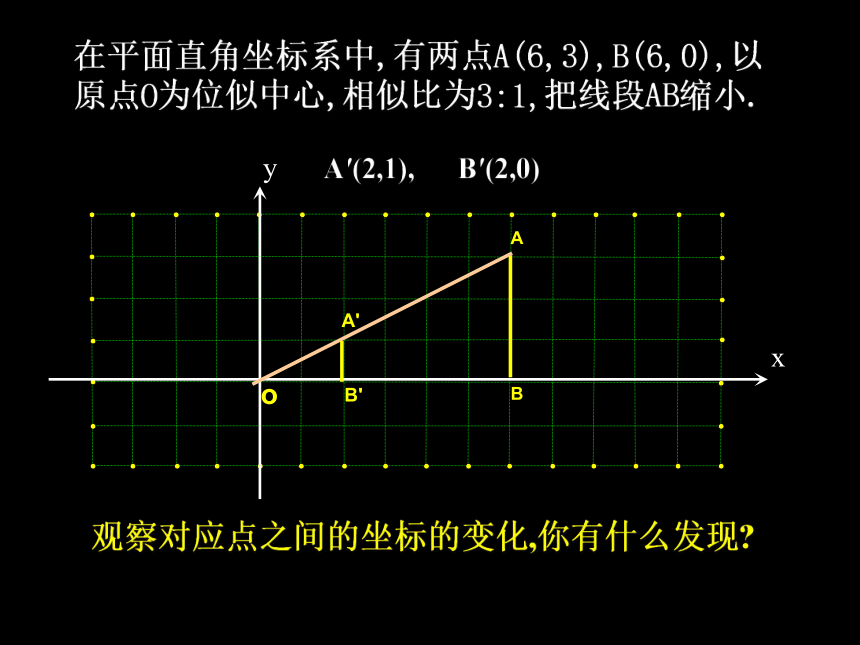
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1), B′(2,0)
观察对应点之间的坐标的变化,你有什么发现
B'
A'
x
y
B
A
o
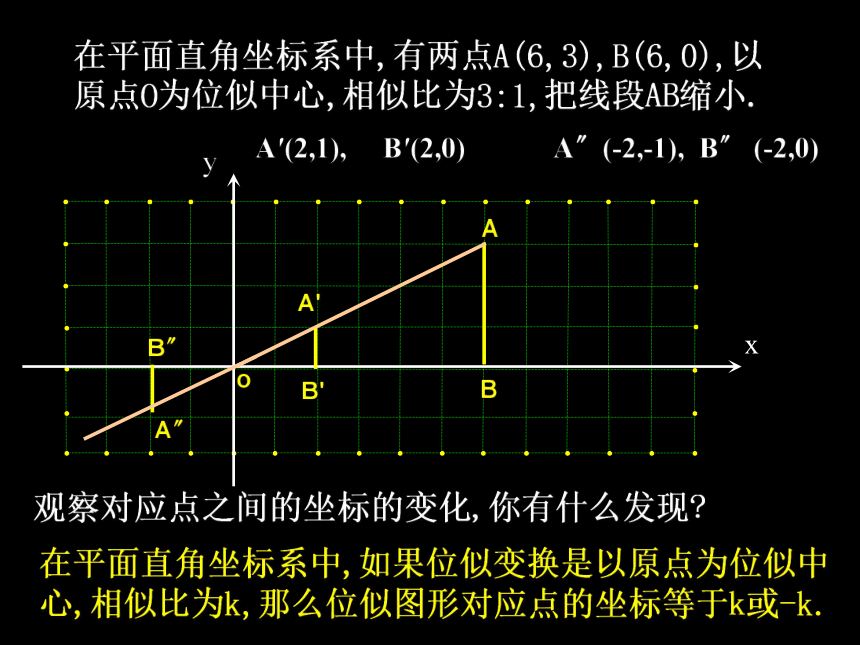
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1), B′(2,0)
A〞
B〞
A〞(-2,-1), B〞 (-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标等于k或-k.
观察对应点之间的坐标的变化,你有什么发现
x
y
o
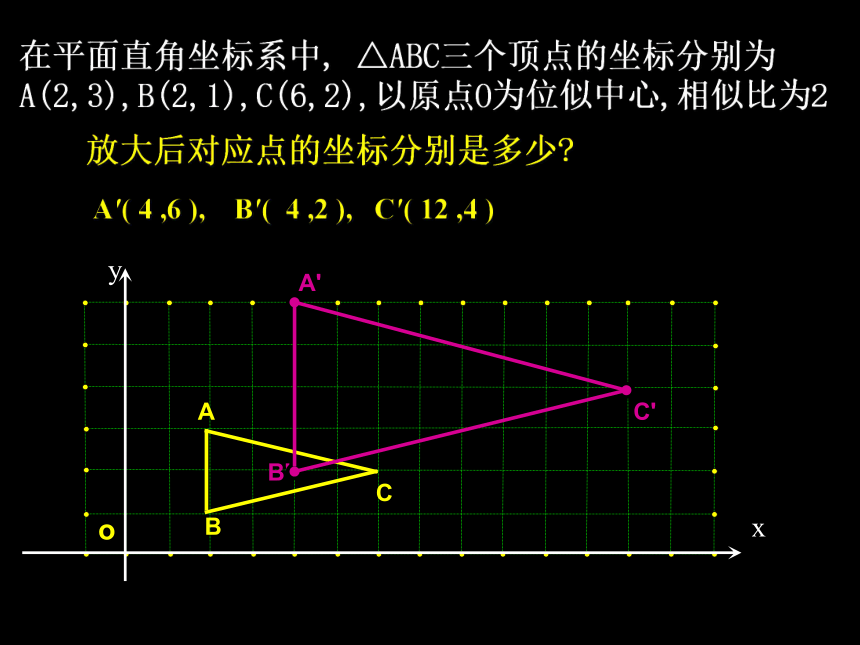
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2
B
A
C
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
放大后对应点的坐标分别是多少
B'
A'
C'
x
y
o
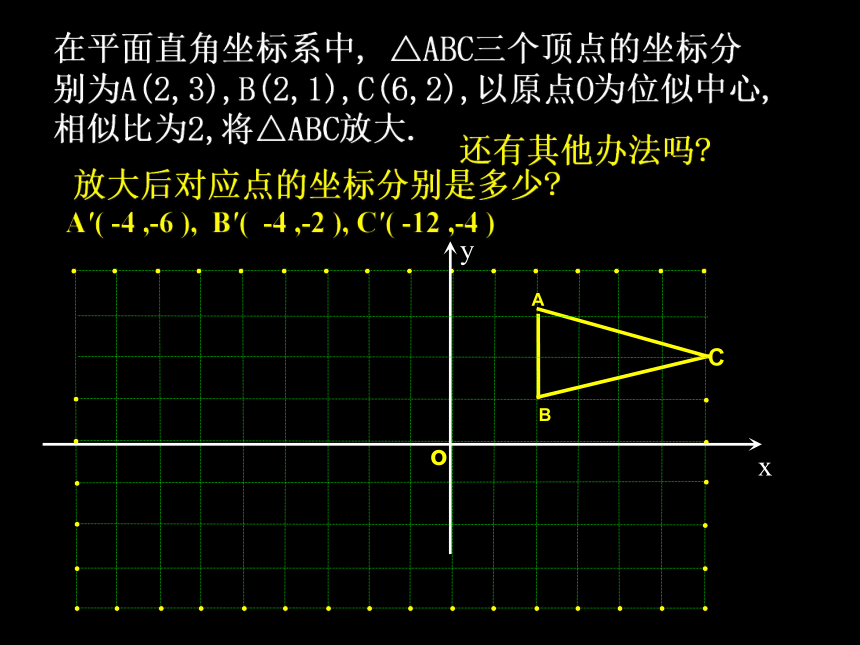
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
B
A
C
放大后对应点的坐标分别是多少
还有其他办法吗
x
y
o
在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗 试试看.
x
y
o
B
如图表示△ABC把它缩小后得到的△COD,求它们的相似比
A
C
D
x
y
o
如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
B
A
C
我们已经学过哪些图形变换?
平移、轴对称、旋转、位似
你能说出它们之间的异同吗?
在下列图案中,你能找出哪些变换
P
如图,以点P为位似中心,将五角星缩小为原来的一半
练习
x
y
o
如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,7),按照下列相似比,分别写出T、U、V各点的坐标.
W
x
y
z
(1)相似比为4;
(2)相似比为 ;
如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形, 这个点P叫做位似中心, 这时的相似比又称为位似比.
1.什么叫位似图形
2.位似图形的性质
位似图形上的任意一对对应点到位似中心的距离之比等于位似比
3.利用位似可以把一个图形放大或缩小
D
E
F
A
O
B
C
如何把三角形ABC放大为原来的2倍
D
E
F
A
O
B
C
对应点连线都交于____________
对应线段_______________________________
位似中心
平行或在一条直线上
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1), B′(2,0)
观察对应点之间的坐标的变化,你有什么发现
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1), B′(2,0)
A〞
B〞
A〞(-2,-1), B〞 (-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标等于k或-k.
观察对应点之间的坐标的变化,你有什么发现
x
y
o
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2
B
A
C
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
放大后对应点的坐标分别是多少
B'
A'
C'
x
y
o
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
B
A
C
放大后对应点的坐标分别是多少
还有其他办法吗
x
y
o
在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗 试试看.
x
y
o
B
如图表示△ABC把它缩小后得到的△COD,求它们的相似比
A
C
D
x
y
o
如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
B
A
C
我们已经学过哪些图形变换?
平移、轴对称、旋转、位似
你能说出它们之间的异同吗?
在下列图案中,你能找出哪些变换
P
如图,以点P为位似中心,将五角星缩小为原来的一半
练习
x
y
o
如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,7),按照下列相似比,分别写出T、U、V各点的坐标.
W
x
y
z
(1)相似比为4;
(2)相似比为 ;
