2021-2022学年青岛新版八年级上册数学第4章 数据分析单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年青岛新版八年级上册数学第4章 数据分析单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览




文档简介
2021-2022学年青岛新版八年级上册数学《第4章 数据分析》单元测试卷
一.选择题
1.若一组数据x1,x2,x3,x4,…,xn的平均数为2000,那么x1+5,x2+5,x3+5,x4+5,……,xn+5这组数据的平均数是( )
A.1999 B.2000 C.2005 D.2006
2.某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.42、42 B.43、42 C.43、43 D.44、43
3.数据1,﹣2,3,﹣4,5,﹣6,p的中位数不可能是( )
A.﹣2 B.1 C.3 D.p
4.在某次月考数学测试中,第一小组6名同学的成绩( 单位:分) 分别为72,49,76,66,85,72,关于这组数据,下列说法正确的是( )
A.众数是76 B.中位数是74 C.平均数是72 D.极差是36
5.从九年级一班参加跳绳考试的同学中随机抽取10名同学的考试成绩如下:193,184,180,186,180,186,184,186,184,186(单位:厘米).下列表述不正确的是( )
A.众数是186 B.平均数是185
C.中位数是185 D.极差是13
6.10个人围成一圈每人想一个自然数,并告诉在他两边的人,然后每人将他两边的人告诉他的数的平均数报出来,报的结果如图,则报13的人心想的数是( )
A.12 B.14 C.16 D.18
7.某校四个绿化小组一天植树的棵数如下:9,9,m,7,已知这组数据的众数和平均数相等,那么这组数据的中位数是( )
A.8 B.9 C.10 D.12
8.某校组织语文、数学、英语、物理四科联赛,满分都是100分,甲、乙、丙三人四科的测试成绩如下表所示,若综合成绩按照语、数、英、物四科测试成绩的1.2:1:1:0.8的比例计分,则综合成绩第一名的是( )
学科 语文 数学 英语 物理
甲 95 85 85 60
乙 80 80 90 80
丙 70 90 80 95
A.甲 B.乙 C.丙 D.不确定
9.数据:a,1,2,3,6的平均数为3,则这组数据的众数是( )
A.2 B.0 C.4 D.3
10.下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
二.填空题
11.5个不同数据1、6、x、5、3的中位数是3,若x为非负整数,则这组数据的平均数是 .
12.小明去商场买作业本,第一次买了4本不同类型的作业本,平均价格是0.85元,第二次买了6本,平均价格是0.95元,则他两次所买练习本的平均价格为 .
13.请你根据H市快餐公司个数统计图和各快餐公司盒饭年销售量的平均数统计图所提供的信息,计算这三年中该地区每年平均销售盒饭 万盒.
14.数据3,2,1,5,4,6的中位数是 .
15.数据11,9,7,10,14,7,6,5的中位数是 ,众数是 .
16.当五个整数从小到大排列后,其中位数是4,如果这组数据的唯一众数是6,那么这组数据可能的最大的和是 .
17.某校九年级安全疏散演习中,各班疏散的时间分别是3分钟,2分40秒,3分20秒,3分30秒,2分45秒.这次演习中,疏散时间的极差为 秒.
18.一个样本2,3,x,5的极差是8,则x的值为 .
19.一个口袋中有15个黑球和若干个白球,从口袋中一次摸出10个球,求出黑球数与10的比值,不断重复上述过程,总共摸了10次,黑球数与10的比值的平均数为1/5,因此可估计口袋中大约有 个白球.
20.已知一个样本0,﹣1,x,1,3它们的平均数是2,则这个样本的中位数是 .
三.解答题
21.一艘客轮往返于南通和上海两港之间,从南通到上海速度为60千米∕时,从上海到南通的速度为40千米∕时,求这艘客轮往返的平均速度是多少?
22.45个互不相等的数的算术平均数是38,其中原有的数40增加了2个,原有的数51增加了4个,原有的数55被去掉,求现在这些数的平均数.
23.自2010年4月1日起,新修订的《机动车驾驶证申领和使用规定》正式实施了.新规定为保障公民的人身安全,对被查酒后驾驶机动车(血液酒精含量超过20毫克/百毫升)的驾驶员加大了处罚力度.某交警大队于4月4日~4月10日这7天共查到12起酒后驾车事件,这12位驾车者血液酒精含量(单位:毫克/百毫升)如下:26,58,29,92,21,43,24,27,36,46,23,31.
(1)请计算这些数据的平均数与极差;
(2)请你运用所学到的统计知识估计新规定实施之后一年内(按365天计算),该交警大队能查到多少起酒后驾车事件?(精确到1起)
(3)该交警大队在新规定实施前的某一周7天内共查到38名司机血液酒精含量超过20毫克/百毫升,平均含量为56毫克/百毫升,请结合相关数据谈谈你的想法.
24.学校广播站要招聘一名播音员,考查形象、知识面、普通话三个项目.按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如下表:
项 目选 手 形 象 知识面 普通话
李 文 70 80 88
孔 明 80 75 x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
25.一组数据8,9,6,m平均数与中位数相等,求m的值.
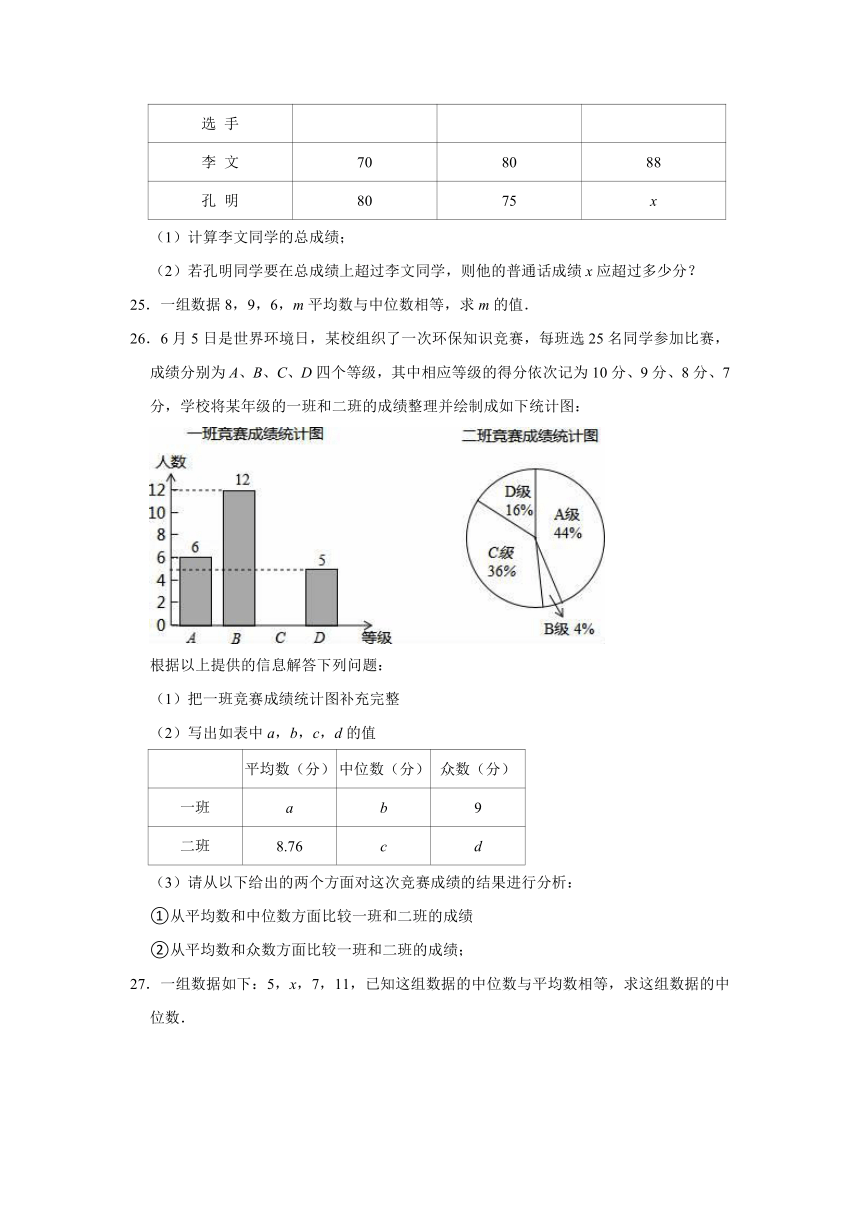
26.6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将某年级的一班和二班的成绩整理并绘制成如下统计图:
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整
(2)写出如表中a,b,c,d的值
平均数(分) 中位数(分) 众数(分)
一班 a b 9
二班 8.76 c d
(3)请从以下给出的两个方面对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩
②从平均数和众数方面比较一班和二班的成绩;
27.一组数据如下:5,x,7,11,已知这组数据的中位数与平均数相等,求这组数据的中位数.
参考答案与试题解析
一.选择题
1.解:设D(x)为平均数,则D(x+5)=2000+5=2005.
故选:C.
2.解:把这组数据排列顺序得:35 38 40 42 44 45 45 47,
则这组数据的中位数为:=43,
=×(35+38+42+44+40+47+45+45)=42,
故选:B.
3.解:若p<﹣2,则数据1,﹣2,3,﹣4,5,﹣6,p的中位数为﹣2;
若﹣2≤p≤1,则数据1,﹣2,3,﹣4,5,﹣6,p的中位数为p;
若p>1,则数据1,﹣2,3,﹣4,5,﹣6,p的中位数为1;
∴中位数不可能为3.
故选:C.
4.解:A、72出现次数最多,故众数应该是72,说法错误;
B、将数据从小到大排列为:49,66,72,72,76,85,故中位数是72,说法错误;
C、平均数=(72+49+76+66+85+72)=70,说法错误;
D、极差为85﹣49=36,说法正确;
故选:D.
5.解:所给数据中186出现次数最多,为4次,故众数为186;
将10名同学的成绩按从小到大的顺序排列为:180,180,184,184,184,186,186,186,186,193,中位数为185;
平均数为==184.9,
极差为:193﹣180=13.
故选:B.
6.解:设报13的人心想的数是x,报5的人心想的数是28﹣x,报7的人心想的数是x﹣16,报9的人心想的数是32﹣x,报11的人心想的数是x﹣12,
所以有x﹣12+x=2×12,
解得x=18.
故选:D.
7.解:∵众数为9,平均数等于众数,
∴(9+9+m+7)=9,
解得m=11,
∴数据按从小到大排列为:7,9,9,11,
∴这组数据的中位数=(9+9)÷2=9.
故选:B.
8.解:由题意知,甲综合成绩=95×1.2+85+85+60×0.8=332分,
乙综合成绩=80×1.2+80+90+80×0.8=330分,
丙综合成绩=70×1.2+90+80+95×0.8=330分,
∴甲综合成绩最高.
故选:A.
9.解:∵数据a,1,2,3,6的平均数为3,
∴a+1+2+3+6=3×5=15,
解得a=3.
其中3出现的次数最多,
因而这组数据的众数是3.
故选:D.
10.解:A、数据3,4,4,7,3的众数是4和3.故错误;
B、数据0,1,2,5,a的中位数因a的大小不确定,故中位数也无法确定.故错误;
C、一组数据的众数和中位数会出现相等的情况.故错误;
D、数据0,5,﹣7,﹣5,7的中位数和平数数都是0.对.
故选:D.
二.填空题
11.解:∵共5个数,中位数是3,且5个数不相同,x为非负整数,
∴x等于0或2.
当x=0时,平均数=(0+1+3+5+6)÷5=3;
当x=2时,平均数=(2+1+3+5+6)÷5=.
故填3或.
12.解:两次所买练习本的平均价格=(0.85×4+0.95×6)÷10=0.91元.
故填0.91元.
13.解:(50×1+59×1.5+80×2)=99.5
即这三年中该地区每年平均销售盒饭99.5万盒.
故填99.5.
14.解:将题目中的数据按照从小到大的顺序排列是:
1、2、3、4、5、6,
故这组数据的中位数是(3+4)=3.5,
故答案为:3.5.
15.解:将数据11,9,7,10,14,7,6,5从小到大重新排列后为:5,6,7,7,9,10,11,14;观察数据可知最中间的数是7,9,它们的平均数是8,所以中位数是8;出现次数最多的是7,所以众数为7.
故填8,7
16.解:因为五个整数从小到大排列后,其中位数是4,这组数据的唯一众数是6.
所以这5个数据分别是x,y,4,6,6,其中x=1或2,y=2或3.
∴这组数据可能的最大的和是2+3+4+6+6=21.
故答案为:21.
17.解:数据中最大的值210,最小值160,所以疏散时间的极差=210﹣160=50(秒).
故填50.
18.解:当x是最大值时:x﹣2=8
解得:x=10
当x是最小值时:5﹣x=8
解得:x=﹣3
∴x等于﹣3或10.
故填﹣3或10.
19.解:由题意知,黑球数与10的比值的平均数为1/5,则说明黑球占总球数的20%,所以总球数为15÷20%=75个,则白球数为75﹣15=60个.
故答案为60.
20.解:∵0,﹣1,x,1,3的平均数是2,
∴x=7,
把0,﹣1,7,1,3按大小顺序排列为﹣1,0,1,3,7,
∴个样本的中位数是1,
故答案为1.
三.解答题
21.解:由题意,设上海到南通的距离为S,
则从南通到上海所用的时间=h,从上海到南通所用的时间=h,
则全程的平均速度==48千米∕时.
22.解:原来45个互不相等的数的和为:38×45=1710,
变化后的数共有45+2+4﹣1=50(个),
所以现在这些数的平均数=(1710+40×2+51×4﹣55)÷50=1939÷50=38.78.
23.解:(1)平均数=(26+58+29+92+21+43+24+27+36+46+23+31)=38(毫克/百毫升),
极差=92﹣21=71(毫克/百毫升);
(2)365÷7×12≈626(起);
(3)与新规定实施前相比,抽查到的司机血液酒精平均含量大大减少,说明人们法律意识增强了,但还要提高认识.
24.解:(1)70×10%+80×40%+88×50%=83(分);
(2)80×10%+75×40%+50% x>83,
∴x>90.
∴李文同学的总成绩是83分,孔明同学要在总成绩上超过李文同学,则他的普通话成绩应超过90分.
25.解:①当m为最大值时,排序为:m,9,8,6.根据题意得=.解得m=11;
②当m为最小值时,排序为:9,8,6,m.根据题意得=.解得m=5;
③当m既不是最大,也不是最小时,排序为:9,8,m,6或9,m,8,6.根据题意得=.解得m=7.
∴m的值为5或7或11.
26.解:(1)一班C等级的人数为25﹣6﹣12﹣5=2(人),
统计图为:
(2)一班的平均数a=(6×10+12×9+2×8+5×7)=8.76(分),
一班的中位数落在B等级,故b=9(分);
二班的中位数落在C等级,故c=8(分);
二班的A等级所占百分比最大,故众数d=10(分);
(3)①从平均数的角度看两班成绩一样,从中数的角度看一班比班班的成绩好,所以一班成绩好.
②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好.
27.解:(1)将这组数据从大到小的顺序排列为11,7,x,5,
处于中间位置的那个数是7,x,
那么由中位数的定义可知,这组数据的中位数是(7+x)÷2,
平均数为(11+7+x+5)÷4,
∵数据11,7,x,5,的中位数与平均数相等,
∴(7+x)÷2=(11+7+x+5)÷4,
解得x=9,大小位置与7对调,不影响结果,符合题意,
此时中位数为(7+9)÷2=8;
(2)将这组数据从大到小的顺序排列后11,7,5,x,
中位数是(5+7)÷2=6,
此时平均数是(11+7+x+5)÷4=6,
解得x=1,符合排列顺序,此时中位数为6;
(3)将这组数据从大到小的顺序排列后x,11,7,5,
中位数是(11+7)÷2=9,
平均数(11+7+x+5)÷4=9,
解得x=13,符合排列顺序,此时中位数是9.
答:这组数据的中位数是6、8或9.
一.选择题
1.若一组数据x1,x2,x3,x4,…,xn的平均数为2000,那么x1+5,x2+5,x3+5,x4+5,……,xn+5这组数据的平均数是( )
A.1999 B.2000 C.2005 D.2006
2.某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.42、42 B.43、42 C.43、43 D.44、43
3.数据1,﹣2,3,﹣4,5,﹣6,p的中位数不可能是( )
A.﹣2 B.1 C.3 D.p
4.在某次月考数学测试中,第一小组6名同学的成绩( 单位:分) 分别为72,49,76,66,85,72,关于这组数据,下列说法正确的是( )
A.众数是76 B.中位数是74 C.平均数是72 D.极差是36
5.从九年级一班参加跳绳考试的同学中随机抽取10名同学的考试成绩如下:193,184,180,186,180,186,184,186,184,186(单位:厘米).下列表述不正确的是( )
A.众数是186 B.平均数是185
C.中位数是185 D.极差是13
6.10个人围成一圈每人想一个自然数,并告诉在他两边的人,然后每人将他两边的人告诉他的数的平均数报出来,报的结果如图,则报13的人心想的数是( )
A.12 B.14 C.16 D.18
7.某校四个绿化小组一天植树的棵数如下:9,9,m,7,已知这组数据的众数和平均数相等,那么这组数据的中位数是( )
A.8 B.9 C.10 D.12
8.某校组织语文、数学、英语、物理四科联赛,满分都是100分,甲、乙、丙三人四科的测试成绩如下表所示,若综合成绩按照语、数、英、物四科测试成绩的1.2:1:1:0.8的比例计分,则综合成绩第一名的是( )
学科 语文 数学 英语 物理
甲 95 85 85 60
乙 80 80 90 80
丙 70 90 80 95
A.甲 B.乙 C.丙 D.不确定
9.数据:a,1,2,3,6的平均数为3,则这组数据的众数是( )
A.2 B.0 C.4 D.3
10.下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
二.填空题
11.5个不同数据1、6、x、5、3的中位数是3,若x为非负整数,则这组数据的平均数是 .
12.小明去商场买作业本,第一次买了4本不同类型的作业本,平均价格是0.85元,第二次买了6本,平均价格是0.95元,则他两次所买练习本的平均价格为 .
13.请你根据H市快餐公司个数统计图和各快餐公司盒饭年销售量的平均数统计图所提供的信息,计算这三年中该地区每年平均销售盒饭 万盒.
14.数据3,2,1,5,4,6的中位数是 .
15.数据11,9,7,10,14,7,6,5的中位数是 ,众数是 .
16.当五个整数从小到大排列后,其中位数是4,如果这组数据的唯一众数是6,那么这组数据可能的最大的和是 .
17.某校九年级安全疏散演习中,各班疏散的时间分别是3分钟,2分40秒,3分20秒,3分30秒,2分45秒.这次演习中,疏散时间的极差为 秒.
18.一个样本2,3,x,5的极差是8,则x的值为 .
19.一个口袋中有15个黑球和若干个白球,从口袋中一次摸出10个球,求出黑球数与10的比值,不断重复上述过程,总共摸了10次,黑球数与10的比值的平均数为1/5,因此可估计口袋中大约有 个白球.
20.已知一个样本0,﹣1,x,1,3它们的平均数是2,则这个样本的中位数是 .
三.解答题
21.一艘客轮往返于南通和上海两港之间,从南通到上海速度为60千米∕时,从上海到南通的速度为40千米∕时,求这艘客轮往返的平均速度是多少?
22.45个互不相等的数的算术平均数是38,其中原有的数40增加了2个,原有的数51增加了4个,原有的数55被去掉,求现在这些数的平均数.
23.自2010年4月1日起,新修订的《机动车驾驶证申领和使用规定》正式实施了.新规定为保障公民的人身安全,对被查酒后驾驶机动车(血液酒精含量超过20毫克/百毫升)的驾驶员加大了处罚力度.某交警大队于4月4日~4月10日这7天共查到12起酒后驾车事件,这12位驾车者血液酒精含量(单位:毫克/百毫升)如下:26,58,29,92,21,43,24,27,36,46,23,31.
(1)请计算这些数据的平均数与极差;
(2)请你运用所学到的统计知识估计新规定实施之后一年内(按365天计算),该交警大队能查到多少起酒后驾车事件?(精确到1起)
(3)该交警大队在新规定实施前的某一周7天内共查到38名司机血液酒精含量超过20毫克/百毫升,平均含量为56毫克/百毫升,请结合相关数据谈谈你的想法.
24.学校广播站要招聘一名播音员,考查形象、知识面、普通话三个项目.按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如下表:
项 目选 手 形 象 知识面 普通话
李 文 70 80 88
孔 明 80 75 x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
25.一组数据8,9,6,m平均数与中位数相等,求m的值.
26.6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将某年级的一班和二班的成绩整理并绘制成如下统计图:
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整
(2)写出如表中a,b,c,d的值
平均数(分) 中位数(分) 众数(分)
一班 a b 9
二班 8.76 c d
(3)请从以下给出的两个方面对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩
②从平均数和众数方面比较一班和二班的成绩;
27.一组数据如下:5,x,7,11,已知这组数据的中位数与平均数相等,求这组数据的中位数.
参考答案与试题解析
一.选择题
1.解:设D(x)为平均数,则D(x+5)=2000+5=2005.
故选:C.
2.解:把这组数据排列顺序得:35 38 40 42 44 45 45 47,
则这组数据的中位数为:=43,
=×(35+38+42+44+40+47+45+45)=42,
故选:B.
3.解:若p<﹣2,则数据1,﹣2,3,﹣4,5,﹣6,p的中位数为﹣2;
若﹣2≤p≤1,则数据1,﹣2,3,﹣4,5,﹣6,p的中位数为p;
若p>1,则数据1,﹣2,3,﹣4,5,﹣6,p的中位数为1;
∴中位数不可能为3.
故选:C.
4.解:A、72出现次数最多,故众数应该是72,说法错误;
B、将数据从小到大排列为:49,66,72,72,76,85,故中位数是72,说法错误;
C、平均数=(72+49+76+66+85+72)=70,说法错误;
D、极差为85﹣49=36,说法正确;
故选:D.
5.解:所给数据中186出现次数最多,为4次,故众数为186;
将10名同学的成绩按从小到大的顺序排列为:180,180,184,184,184,186,186,186,186,193,中位数为185;
平均数为==184.9,
极差为:193﹣180=13.
故选:B.
6.解:设报13的人心想的数是x,报5的人心想的数是28﹣x,报7的人心想的数是x﹣16,报9的人心想的数是32﹣x,报11的人心想的数是x﹣12,
所以有x﹣12+x=2×12,
解得x=18.
故选:D.
7.解:∵众数为9,平均数等于众数,
∴(9+9+m+7)=9,
解得m=11,
∴数据按从小到大排列为:7,9,9,11,
∴这组数据的中位数=(9+9)÷2=9.
故选:B.
8.解:由题意知,甲综合成绩=95×1.2+85+85+60×0.8=332分,
乙综合成绩=80×1.2+80+90+80×0.8=330分,
丙综合成绩=70×1.2+90+80+95×0.8=330分,
∴甲综合成绩最高.
故选:A.
9.解:∵数据a,1,2,3,6的平均数为3,
∴a+1+2+3+6=3×5=15,
解得a=3.
其中3出现的次数最多,
因而这组数据的众数是3.
故选:D.
10.解:A、数据3,4,4,7,3的众数是4和3.故错误;
B、数据0,1,2,5,a的中位数因a的大小不确定,故中位数也无法确定.故错误;
C、一组数据的众数和中位数会出现相等的情况.故错误;
D、数据0,5,﹣7,﹣5,7的中位数和平数数都是0.对.
故选:D.
二.填空题
11.解:∵共5个数,中位数是3,且5个数不相同,x为非负整数,
∴x等于0或2.
当x=0时,平均数=(0+1+3+5+6)÷5=3;
当x=2时,平均数=(2+1+3+5+6)÷5=.
故填3或.
12.解:两次所买练习本的平均价格=(0.85×4+0.95×6)÷10=0.91元.
故填0.91元.
13.解:(50×1+59×1.5+80×2)=99.5
即这三年中该地区每年平均销售盒饭99.5万盒.
故填99.5.
14.解:将题目中的数据按照从小到大的顺序排列是:
1、2、3、4、5、6,
故这组数据的中位数是(3+4)=3.5,
故答案为:3.5.
15.解:将数据11,9,7,10,14,7,6,5从小到大重新排列后为:5,6,7,7,9,10,11,14;观察数据可知最中间的数是7,9,它们的平均数是8,所以中位数是8;出现次数最多的是7,所以众数为7.
故填8,7
16.解:因为五个整数从小到大排列后,其中位数是4,这组数据的唯一众数是6.
所以这5个数据分别是x,y,4,6,6,其中x=1或2,y=2或3.
∴这组数据可能的最大的和是2+3+4+6+6=21.
故答案为:21.
17.解:数据中最大的值210,最小值160,所以疏散时间的极差=210﹣160=50(秒).
故填50.
18.解:当x是最大值时:x﹣2=8
解得:x=10
当x是最小值时:5﹣x=8
解得:x=﹣3
∴x等于﹣3或10.
故填﹣3或10.
19.解:由题意知,黑球数与10的比值的平均数为1/5,则说明黑球占总球数的20%,所以总球数为15÷20%=75个,则白球数为75﹣15=60个.
故答案为60.
20.解:∵0,﹣1,x,1,3的平均数是2,
∴x=7,
把0,﹣1,7,1,3按大小顺序排列为﹣1,0,1,3,7,
∴个样本的中位数是1,
故答案为1.
三.解答题
21.解:由题意,设上海到南通的距离为S,
则从南通到上海所用的时间=h,从上海到南通所用的时间=h,
则全程的平均速度==48千米∕时.
22.解:原来45个互不相等的数的和为:38×45=1710,
变化后的数共有45+2+4﹣1=50(个),
所以现在这些数的平均数=(1710+40×2+51×4﹣55)÷50=1939÷50=38.78.
23.解:(1)平均数=(26+58+29+92+21+43+24+27+36+46+23+31)=38(毫克/百毫升),
极差=92﹣21=71(毫克/百毫升);
(2)365÷7×12≈626(起);
(3)与新规定实施前相比,抽查到的司机血液酒精平均含量大大减少,说明人们法律意识增强了,但还要提高认识.
24.解:(1)70×10%+80×40%+88×50%=83(分);
(2)80×10%+75×40%+50% x>83,
∴x>90.
∴李文同学的总成绩是83分,孔明同学要在总成绩上超过李文同学,则他的普通话成绩应超过90分.
25.解:①当m为最大值时,排序为:m,9,8,6.根据题意得=.解得m=11;
②当m为最小值时,排序为:9,8,6,m.根据题意得=.解得m=5;
③当m既不是最大,也不是最小时,排序为:9,8,m,6或9,m,8,6.根据题意得=.解得m=7.
∴m的值为5或7或11.
26.解:(1)一班C等级的人数为25﹣6﹣12﹣5=2(人),
统计图为:
(2)一班的平均数a=(6×10+12×9+2×8+5×7)=8.76(分),
一班的中位数落在B等级,故b=9(分);
二班的中位数落在C等级,故c=8(分);
二班的A等级所占百分比最大,故众数d=10(分);
(3)①从平均数的角度看两班成绩一样,从中数的角度看一班比班班的成绩好,所以一班成绩好.
②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好.
27.解:(1)将这组数据从大到小的顺序排列为11,7,x,5,
处于中间位置的那个数是7,x,
那么由中位数的定义可知,这组数据的中位数是(7+x)÷2,
平均数为(11+7+x+5)÷4,
∵数据11,7,x,5,的中位数与平均数相等,
∴(7+x)÷2=(11+7+x+5)÷4,
解得x=9,大小位置与7对调,不影响结果,符合题意,
此时中位数为(7+9)÷2=8;
(2)将这组数据从大到小的顺序排列后11,7,5,x,
中位数是(5+7)÷2=6,
此时平均数是(11+7+x+5)÷4=6,
解得x=1,符合排列顺序,此时中位数为6;
(3)将这组数据从大到小的顺序排列后x,11,7,5,
中位数是(11+7)÷2=9,
平均数(11+7+x+5)÷4=9,
解得x=13,符合排列顺序,此时中位数是9.
答:这组数据的中位数是6、8或9.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
