2021-2022学年高一上学期数学人教B版(2019)必修第二册4.1指数与指数函数新课讲义
文档属性
| 名称 | 2021-2022学年高一上学期数学人教B版(2019)必修第二册4.1指数与指数函数新课讲义 |
|
|
| 格式 | docx | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 10:27:31 | ||
图片预览





文档简介
4.1指数与指数函数(新课)
知识梳理
整数指数幂的概念及运算性质
1.根式运算
(1)
2.整数指数幂的概念
(1)(2)(3)
3.运算法则
(1);(2);(3);(4).
分数指数幂的概念和运算法则
(1)(2)(3)
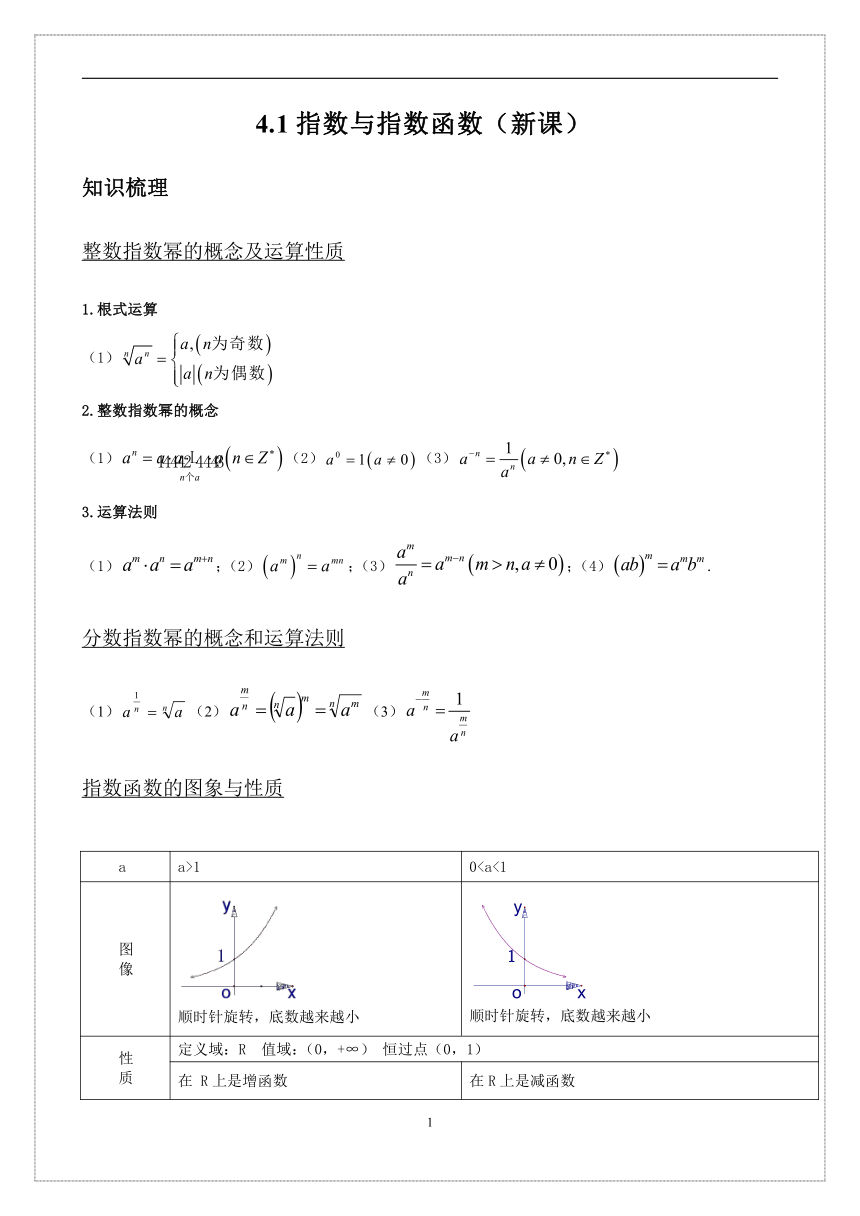
指数函数的图象与性质
a a>1 0图像 顺时针旋转,底数越来越小 顺时针旋转,底数越来越小
性质 定义域:R 值域:(0,+∞) 恒过点(0,1)
在 R上是增函数 在R上是减函数
典例解析
考点一:根式
例1:计算:(1)(3);(2).
变式1:化简:
变式2:化简:
考点二:指数运算、化简、求值
例2:用分数指数幂形式表示下列各式(式中):
(1); (2); (3); (4)。
变式1:把下列根式用指数形式表示出来,并化简
(1) (2)
变式2:把下列子式化成分数指数幂:
(1) (2)
例3:计算:
(1) (2)
变式1:计算下列算式:
变式2:化简下列各式.
(1) (2)
例4:化简:
变式1:已知,,且,求的值.
变式2:已知,求及的值.
考点三:函数的定义域、值域
例5:求下列函数的定义域、值域
(1);(2);(3);(4)(为大于1的常数)
变式1:求下列函数的定义域
(1);(2);
变式2:求下列函数的定义域
(1);(2)
考点四:指数函数的单调性及其应用
例6:讨论函数的单调性,并求其值域.
变式1:求函数的单调区间及值域.
变式2:求函数(其中,且)的单调区间.
例7:讨论函数的单调性
变式1:求函数的单调区间并求出它的值域.
变式2:若函数满足,且在上单调递增,则实数的最小值等于
例8:比较下列几组函数大小
(1);(2);(3);
变式1:比较
变式2:如果,求的取值范围.
考点五:判断函数的奇偶性
例9:判断函数的奇偶性:
变式1:判断下列函数的奇偶性:(为奇函数).
变式2:判断函数的奇偶性:
考点六:指数函数的图象问题
例10:如图的曲线是指数函数的图象,而,则图象对应的函数的底数依次是________、________、________、________.
变式1:已知函数.
(1)作出函数的图象;
(2)指出该函数的单调递增区间;
(3)求函数的值域.
变式2:若直线与的图象有两个公共点,则的取值范围是.
考点七:分段函数
例11:已知函数,则使得成立的的取值范围是_________.
变式1.设函数若,则的取值范围是_________.
变式2:设,则
考点八:恒过定点问题
例12:函数恒过定点____________。
变式1:函数恒过定点____________。
变式2:函数恒过定点____________。
巩固练习
1.化简的结果是( )
A. B. C. D.
2.若,且,则的值等于( )
A. B. C. D.2
3.化简,结果是( )
A.6x―6 B.―6x+6 C.―4 D.4
4.已知定义在上的奇函数和偶函数满足
,若,则( )
A. 2 B. C. D.
5.函数在R上是减函数,则的取值范围是( )
A. B. C. D.
6.已知,下列不等式(1);(2);(3);(4);(5)中恒成立的有( )
A.1个 B.2个 C.3个 D.4个
7.用表示三个数中的最小值.设,则的最大值为( )
A.4 B.5 C.6 D.7
8.函数的值域是( )
A. B. C. D.
9.已知,则函数的图象必定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.计算(1); (2)
11.求值:(1); (2);
12.比较大小
13. .
14.化简的结果是
15.已知,则= .
16.函数的值域是区间,则与的大小关系是 .
17.函数的值域是 .
18.方程的实数解的个数为 .
19.计算:
; (2).
20计算:;
21.设,解关于的不等式.
22.已知为定义在 上的奇函数,当时,函数解析式为.
(1)求在上的解析式;
(2)求在上的最值.
23.已知函数的定义域是[0,3],设
(1)求的解析式及定义域;
(2)若,求函数的最大值和最小值.
4.1指数与指数函数答案
典例解析
例1:(1)2(2) 变式1: 变式2:4
例2:(1)(2)(3)(4) 变式1:(1)(2) 变式2:(1)(2)
例3:(1)3(2)0 变式1:112 变式2:(1)(2)0.09
例4: 变式1: 变式2:
例5:(1)R (2)R (3)(4)
变式1:(1)R (2) 变式2:(1) (2)
例6: 值域 变1 值域变2略
例7: 值域 变1:值域 变2:1
例8:(1)(2)(3)
变式1: 变式2:
例9:奇函数 变式1:偶函数 变式2:偶函数
例10: 变式1:(1)略(2)(3)变式2:
例11: 变式1: 变式2: :
例12: 变式1: 变式2:
巩固练习
B
C
D
B
D
C
C
D
A
(1)27 (2)
(1)-2(2)2
2
(1)6(2)
0
(1)(2)最小-2 最大0
(1),(2)最大-3 最小-4
8
9
知识梳理
整数指数幂的概念及运算性质
1.根式运算
(1)
2.整数指数幂的概念
(1)(2)(3)
3.运算法则
(1);(2);(3);(4).
分数指数幂的概念和运算法则
(1)(2)(3)
指数函数的图象与性质
a a>1 0
性质 定义域:R 值域:(0,+∞) 恒过点(0,1)
在 R上是增函数 在R上是减函数
典例解析
考点一:根式
例1:计算:(1)(3);(2).
变式1:化简:
变式2:化简:
考点二:指数运算、化简、求值
例2:用分数指数幂形式表示下列各式(式中):
(1); (2); (3); (4)。
变式1:把下列根式用指数形式表示出来,并化简
(1) (2)
变式2:把下列子式化成分数指数幂:
(1) (2)
例3:计算:
(1) (2)
变式1:计算下列算式:
变式2:化简下列各式.
(1) (2)
例4:化简:
变式1:已知,,且,求的值.
变式2:已知,求及的值.
考点三:函数的定义域、值域
例5:求下列函数的定义域、值域
(1);(2);(3);(4)(为大于1的常数)
变式1:求下列函数的定义域
(1);(2);
变式2:求下列函数的定义域
(1);(2)
考点四:指数函数的单调性及其应用
例6:讨论函数的单调性,并求其值域.
变式1:求函数的单调区间及值域.
变式2:求函数(其中,且)的单调区间.
例7:讨论函数的单调性
变式1:求函数的单调区间并求出它的值域.
变式2:若函数满足,且在上单调递增,则实数的最小值等于
例8:比较下列几组函数大小
(1);(2);(3);
变式1:比较
变式2:如果,求的取值范围.
考点五:判断函数的奇偶性
例9:判断函数的奇偶性:
变式1:判断下列函数的奇偶性:(为奇函数).
变式2:判断函数的奇偶性:
考点六:指数函数的图象问题
例10:如图的曲线是指数函数的图象,而,则图象对应的函数的底数依次是________、________、________、________.
变式1:已知函数.
(1)作出函数的图象;
(2)指出该函数的单调递增区间;
(3)求函数的值域.
变式2:若直线与的图象有两个公共点,则的取值范围是.
考点七:分段函数
例11:已知函数,则使得成立的的取值范围是_________.
变式1.设函数若,则的取值范围是_________.
变式2:设,则
考点八:恒过定点问题
例12:函数恒过定点____________。
变式1:函数恒过定点____________。
变式2:函数恒过定点____________。
巩固练习
1.化简的结果是( )
A. B. C. D.
2.若,且,则的值等于( )
A. B. C. D.2
3.化简,结果是( )
A.6x―6 B.―6x+6 C.―4 D.4
4.已知定义在上的奇函数和偶函数满足
,若,则( )
A. 2 B. C. D.
5.函数在R上是减函数,则的取值范围是( )
A. B. C. D.
6.已知,下列不等式(1);(2);(3);(4);(5)中恒成立的有( )
A.1个 B.2个 C.3个 D.4个
7.用表示三个数中的最小值.设,则的最大值为( )
A.4 B.5 C.6 D.7
8.函数的值域是( )
A. B. C. D.
9.已知,则函数的图象必定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.计算(1); (2)
11.求值:(1); (2);
12.比较大小
13. .
14.化简的结果是
15.已知,则= .
16.函数的值域是区间,则与的大小关系是 .
17.函数的值域是 .
18.方程的实数解的个数为 .
19.计算:
; (2).
20计算:;
21.设,解关于的不等式.
22.已知为定义在 上的奇函数,当时,函数解析式为.
(1)求在上的解析式;
(2)求在上的最值.
23.已知函数的定义域是[0,3],设
(1)求的解析式及定义域;
(2)若,求函数的最大值和最小值.
4.1指数与指数函数答案
典例解析
例1:(1)2(2) 变式1: 变式2:4
例2:(1)(2)(3)(4) 变式1:(1)(2) 变式2:(1)(2)
例3:(1)3(2)0 变式1:112 变式2:(1)(2)0.09
例4: 变式1: 变式2:
例5:(1)R (2)R (3)(4)
变式1:(1)R (2) 变式2:(1) (2)
例6: 值域 变1 值域变2略
例7: 值域 变1:值域 变2:1
例8:(1)(2)(3)
变式1: 变式2:
例9:奇函数 变式1:偶函数 变式2:偶函数
例10: 变式1:(1)略(2)(3)变式2:
例11: 变式1: 变式2: :
例12: 变式1: 变式2:
巩固练习
B
C
D
B
D
C
C
D
A
(1)27 (2)
(1)-2(2)2
2
(1)6(2)
0
(1)(2)最小-2 最大0
(1),(2)最大-3 最小-4
8
9
