2021-2022学年高一上学期数学人教B版(2019)必修第二册4.3 指数函数与对数函数的关系新课讲义
文档属性
| 名称 | 2021-2022学年高一上学期数学人教B版(2019)必修第二册4.3 指数函数与对数函数的关系新课讲义 |

|
|
| 格式 | docx | ||
| 文件大小 | 317.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览


文档简介
4.3指数函数与对数函数的关系(新课)
知识梳理
反函数的概念
1.定义:一般的在函数中,给定值域中的任何一个y的值,只有惟一的x与之对应,那么x是y的函数,这个函数称为的反函数。
反函数的性质
1.一般的,函数的反函数记做,的定义域与的值域相同;的值域与的定义域相同,与的图像关于直线对称;如果点在函数上,那么点一定在上。
2.如果是单调函数,那么一定是单调函数;如果是增函数,那么一定也是增函数;如果是减函数,那么一定也是减函数。
典例解析
考点一:求反函数的解析式
例1:求函数的反函数的解析式。
变式1.函数的反函数为( )
变式2. 已知函数f(x)=2x的反函数为y=g(x),则g()的值为( )
A. B. 1 C. 12 D. 2
例2.设函数(其中为常数)的反函数为,若函数的图像经过点,则方程的解为____.
变式1.若点既在图象上,又在其反函数的图象上,则____
变式2.已知函数=的图象经过点(1,3),其反函数的图象经过点(2.0),则=___________.
考点二:反函数的性质
例3. 函数且的反函数过点,则______.
变式1:已知点在函数的反函数的图象上.
(1)求实数的值;
(2)若,求的取值范围.
变:2:若函数是函数的反函数,且,则( )
例4. 若函数的图象位于第一、二象限,则它的反函数的图象位于( )
A. 第一、二象限 B. 第三、四象限 C. 第二、三象限 D. 第一、四象限
变式1. 若函数的图象与函数的图象关于直线对称,则( )
A. 10 B. -1 C. 2 D. -2
变式2.函数的图像与函数的图像关于直线对称,则的单调减区间为 ___________
考点三:反函数的图像
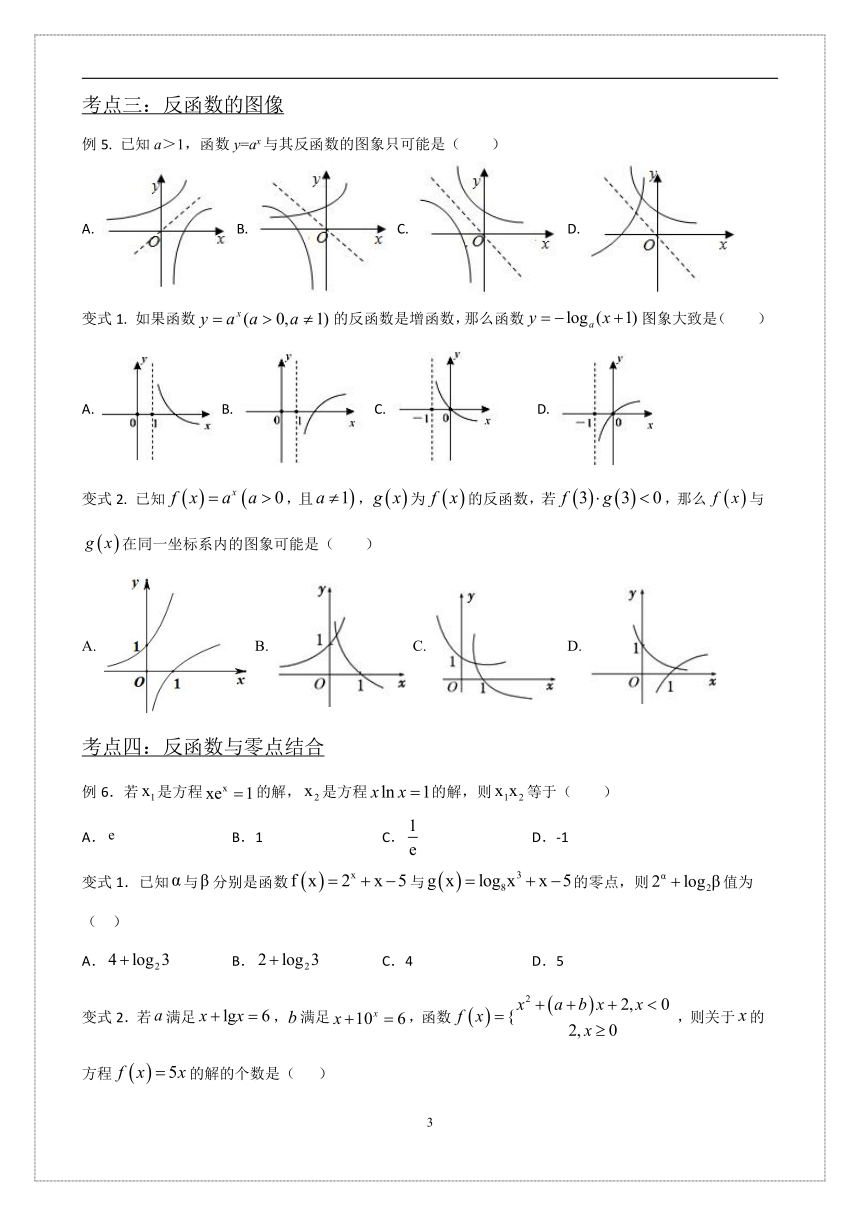
例5. 已知a>1,函数y=ax与其反函数的图象只可能是( )
A. B. C. D.
变式1. 如果函数的反函数是增函数,那么函数图象大致是( )
A. B. C. D.
变式2. 已知,且,为的反函数,若,那么与在同一坐标系内的图象可能是( )
A. B. C. D.
考点四:反函数与零点结合
例6.若是方程的解,是方程的解,则等于( )
A. B.1 C. D.-1
变式1.已知与分别是函数与的零点,则值为( )
A. B. C.4 D.5
变式2.若满足,满足,函数,则关于的方程的解的个数是( )
A.4 B.3 C.2 D.1
巩固练习
1. 已知函数的反函数为,.求的解析式,并指出的定义域;
2.函数的图象过点,则它的反函数的图象过点( )
3.已知函数,若函数是的反函数,则( )
A.1 B.2 C.3 D.4
4.已知函数是奇函数,当时,函数的图象与函数的图象关于对称,则 ( )
A.-7 B.-9 C.-11 D.-13
5.若函数的图像与函数的图像关于直线对称,则( )
A. B. C. D.
6.已知函数的反函数是,则
A. B. C. D.
7.函数存在反函数是函数为单调函数的( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
8.已知函数,则( )
A.0 B.1 C.2 D.3
9.若函数的反函数的图象经过点,则实数a等于( )
A.1 B.2 C.3 D.4
10.函数的反函数为___________
11.函数的反函数是______.
12.()的反函数________
13.函数,的反函数为______.
14.若函数的图象恒过点,则函数的图象一定经过定点______.
4.3指数函数与对数函数的关系答案
典例解析
例1:
变式1.D
变式2.A
例2.
变式1.
变式2.
例2:3
变式1:(1)1(2)
变式2:A
例3. D
变式1. C
变式2.(0,1)
例4. A
变式1. C
变式2. C
例5.B
变式1.D
变式2.D
巩固练习
1.;定义域为 ;
2.D
3.B
4.C
5.C
6.D
7.B
8.C
9.C
10.
11.
12.()
13.,
14.4
1
知识梳理
反函数的概念
1.定义:一般的在函数中,给定值域中的任何一个y的值,只有惟一的x与之对应,那么x是y的函数,这个函数称为的反函数。
反函数的性质
1.一般的,函数的反函数记做,的定义域与的值域相同;的值域与的定义域相同,与的图像关于直线对称;如果点在函数上,那么点一定在上。
2.如果是单调函数,那么一定是单调函数;如果是增函数,那么一定也是增函数;如果是减函数,那么一定也是减函数。
典例解析
考点一:求反函数的解析式
例1:求函数的反函数的解析式。
变式1.函数的反函数为( )
变式2. 已知函数f(x)=2x的反函数为y=g(x),则g()的值为( )
A. B. 1 C. 12 D. 2
例2.设函数(其中为常数)的反函数为,若函数的图像经过点,则方程的解为____.
变式1.若点既在图象上,又在其反函数的图象上,则____
变式2.已知函数=的图象经过点(1,3),其反函数的图象经过点(2.0),则=___________.
考点二:反函数的性质
例3. 函数且的反函数过点,则______.
变式1:已知点在函数的反函数的图象上.
(1)求实数的值;
(2)若,求的取值范围.
变:2:若函数是函数的反函数,且,则( )
例4. 若函数的图象位于第一、二象限,则它的反函数的图象位于( )
A. 第一、二象限 B. 第三、四象限 C. 第二、三象限 D. 第一、四象限
变式1. 若函数的图象与函数的图象关于直线对称,则( )
A. 10 B. -1 C. 2 D. -2
变式2.函数的图像与函数的图像关于直线对称,则的单调减区间为 ___________
考点三:反函数的图像
例5. 已知a>1,函数y=ax与其反函数的图象只可能是( )
A. B. C. D.
变式1. 如果函数的反函数是增函数,那么函数图象大致是( )
A. B. C. D.
变式2. 已知,且,为的反函数,若,那么与在同一坐标系内的图象可能是( )
A. B. C. D.
考点四:反函数与零点结合
例6.若是方程的解,是方程的解,则等于( )
A. B.1 C. D.-1
变式1.已知与分别是函数与的零点,则值为( )
A. B. C.4 D.5
变式2.若满足,满足,函数,则关于的方程的解的个数是( )
A.4 B.3 C.2 D.1
巩固练习
1. 已知函数的反函数为,.求的解析式,并指出的定义域;
2.函数的图象过点,则它的反函数的图象过点( )
3.已知函数,若函数是的反函数,则( )
A.1 B.2 C.3 D.4
4.已知函数是奇函数,当时,函数的图象与函数的图象关于对称,则 ( )
A.-7 B.-9 C.-11 D.-13
5.若函数的图像与函数的图像关于直线对称,则( )
A. B. C. D.
6.已知函数的反函数是,则
A. B. C. D.
7.函数存在反函数是函数为单调函数的( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
8.已知函数,则( )
A.0 B.1 C.2 D.3
9.若函数的反函数的图象经过点,则实数a等于( )
A.1 B.2 C.3 D.4
10.函数的反函数为___________
11.函数的反函数是______.
12.()的反函数________
13.函数,的反函数为______.
14.若函数的图象恒过点,则函数的图象一定经过定点______.
4.3指数函数与对数函数的关系答案
典例解析
例1:
变式1.D
变式2.A
例2.
变式1.
变式2.
例2:3
变式1:(1)1(2)
变式2:A
例3. D
变式1. C
变式2.(0,1)
例4. A
变式1. C
变式2. C
例5.B
变式1.D
变式2.D
巩固练习
1.;定义域为 ;
2.D
3.B
4.C
5.C
6.D
7.B
8.C
9.C
10.
11.
12.()
13.,
14.4
1
