2021-2022学年高一上学期数学人教B版(2019)必修第二册4.4幂函数新课讲义
文档属性
| 名称 | 2021-2022学年高一上学期数学人教B版(2019)必修第二册4.4幂函数新课讲义 |

|
|
| 格式 | docx | ||
| 文件大小 | 393.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 10:31:06 | ||
图片预览




文档简介
4.4幂函数及图象变换(新课)
知识梳理
幂函数概念
形如的函数,叫做幂函数,其中为常数.
幂函数的图象及性质
作出下列函数的图象:
(1);(2);(3);(4);(5).
初等函数图象变换
1.平移变换
图象左、右平移
图象上、下平移
2.对称变换
,图象关于轴对称
,图象关于轴对称
3.翻折变换:
,把轴右边的图象保留,然后将轴左边部分关于轴对称
把轴上方的图象保留,轴下方的图象关于轴对称
典例解析
考点一:求函数解析式
例1.已知幂函数的图象过点,则 ______________.
变式1:已知幂函数的图象过点,则__________.
变式2.已知幂函数(k∈R,a∈R)的图象过点,则k+a=( )
A. B.1 C. D.2
考点二:幂函数的定义域
例2.函数的定义域是 .
变式1.函数的定义域是( )
A. B. C. D.
变式2.函数的定义域是( )
A. B. C. D.
考点三:幂函数的图象
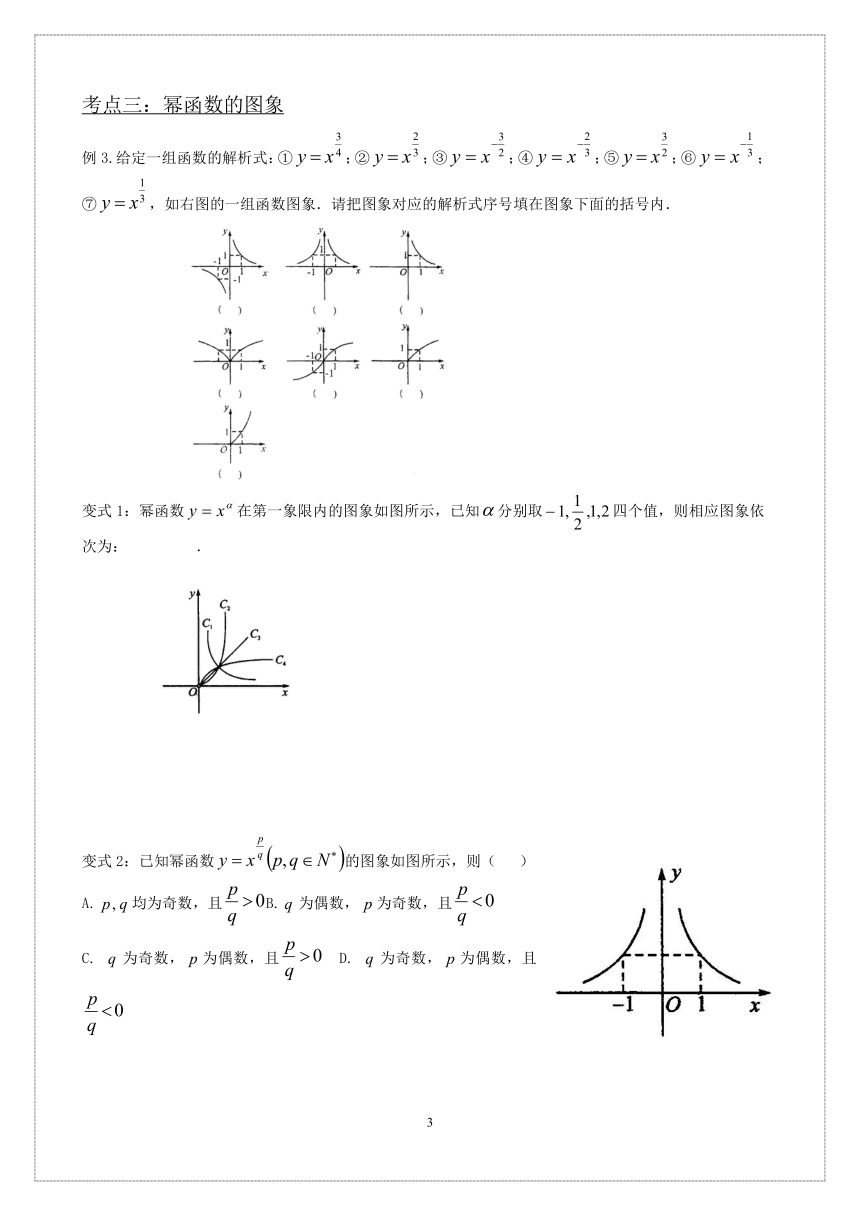
例3.给定一组函数的解析式:①;②;③;④;⑤;⑥;⑦,如右图的一组函数图象.请把图象对应的解析式序号填在图象下面的括号内.
变式1:幂函数在第一象限内的图象如图所示,已知分别取四个值,则相应图象依次为: .
变式2:已知幂函数的图象如图所示,则( )
A.均为奇数,且B.为偶数,为奇数,且
C. 为奇数,为偶数,且 D. 为奇数,为偶数,且
考点四:比较大小
例4.比较的大小.
变式1.设,,中,则a,b,c的大小关系是( )
A. B. C. D.
变式2.已知,则,,的从大到小的顺序是______________.
考点五:求参数的范围
例5.若,求实数的取值范围.
变式1.已知,则的取值范围是( )
A. B. C. D.
变式2.已知幂函数过点,且,则实数k的取值范围是_____.
考点六:幂函数的应用
例6.(2015秋 西宁校级期中)已知幂函数在上单调递增,函数.
(1)求的值;
(2)当时,记的值域分别为集合,若,求实数的取值范围.
变式1. 设,已知函数在上是增函数.
(1)求函数的解析式;
(2)设,试讨论在上的单调性,并求在区间上的最值.
变式2.已知函数为偶函数,且.
(1)求函数的解析式;
(2)若在区间上为增函数,求实数的取值范围.
考点七:基本初等函数图象变换
例7.作出下列函数的图象:
(1) ; (2) ; (3) .
变式1:作出的图象.
变式2:作函数的图象.
巩固练习
1.幂函数的图象经过点,则_________.
2.函数的定义域为__________.
3.已知,,,则( )
A. B. C. D.
4.设,使为奇函数且在上单调递减的的值个数( ).
A. 1 B. 2 C. 3 D. 4
5.当时,下列函数的图象全在直线下方的偶函数是( ).
A. B. C. D.
6.如果是幂函数,则在其定义域上是( ).
A.增函数 B. 在上是增函数,在上是减函数
C.减函数 D.在上是减函数,在上也是减函数
7. 如图所示,幂函数在第一象限的图象,比较的大小( )
A.
B.
C.
D.
8. 三个数,,的大小顺序是( )
A.c9.若幂函数存在反函数,且反函数的图象经过则的表达式为( )
A. B. C. D.
10.如图曲线是幂函数在第一象限内的图象,已知取四个值,相应于曲线的依次为( )
11.下列命题中正确的是( )
幂函数的图象不经过点
幂函数的图象都经过点和点
若幂函数是奇函数,则是定义域上的增函数
幂函数的图象不可能出现在第四象限
12.函数的图象大致为( )
13.已知幂函数,若,则的取值范围是
14.幂函数在(0,+∞)上为增函数,则m=________.
15.(2015秋 湖南长沙期末)已知幂函数的图象关于轴对称,且在区间上是减函数,求函数的解析式.
16.已知幂函数的图象关于y轴对称,并且f(x)在第一象限是单调递减函数.
(1)求m的值;
(2)解不等式f(1-2x)≥f(2).
17.已知函数(m∈Z)是偶函数,且f(x)在(0,+∞)上单调递增.
(1)求m的值,并确定f(x)的解析式;
(2),求g(x)的定义域和值域.
18.已知幂函数在上是增函数,且在其定义域内是偶函数.
(1)求的值,并写出相应的函数
(2)对于(1)中求得的函数,设函数,问是否存在实数,使得在区间上是减函数,且在上是增函数,若存在,请求出来,若不存在,请说明理由。
4.4幂函数答案
典例解析
例1.
变式1:
变式2:A
例2.
变式1.C
变式2.B
例3:6432715
变式1:-1 2 1
变式2:D
例4:< <
变式1.C
变式2.
例5:
变式1.B
变式2.
例6:(1)0(2)
变式1:(1)(2)
变式2:(1)(2)
例7:略
变式1:略
变式2:略
巩固练习
1.
2.
3.A
4.A
5.B
6.D
7.D
8.B
9.B
10.A
11.D
12.C
13.
14.2
15:
16.(1)1(2)
17.(1)1 (2)
18.(1)1 (2)
8
9
知识梳理
幂函数概念
形如的函数,叫做幂函数,其中为常数.
幂函数的图象及性质
作出下列函数的图象:
(1);(2);(3);(4);(5).
初等函数图象变换
1.平移变换
图象左、右平移
图象上、下平移
2.对称变换
,图象关于轴对称
,图象关于轴对称
3.翻折变换:
,把轴右边的图象保留,然后将轴左边部分关于轴对称
把轴上方的图象保留,轴下方的图象关于轴对称
典例解析
考点一:求函数解析式
例1.已知幂函数的图象过点,则 ______________.
变式1:已知幂函数的图象过点,则__________.
变式2.已知幂函数(k∈R,a∈R)的图象过点,则k+a=( )
A. B.1 C. D.2
考点二:幂函数的定义域
例2.函数的定义域是 .
变式1.函数的定义域是( )
A. B. C. D.
变式2.函数的定义域是( )
A. B. C. D.
考点三:幂函数的图象
例3.给定一组函数的解析式:①;②;③;④;⑤;⑥;⑦,如右图的一组函数图象.请把图象对应的解析式序号填在图象下面的括号内.
变式1:幂函数在第一象限内的图象如图所示,已知分别取四个值,则相应图象依次为: .
变式2:已知幂函数的图象如图所示,则( )
A.均为奇数,且B.为偶数,为奇数,且
C. 为奇数,为偶数,且 D. 为奇数,为偶数,且
考点四:比较大小
例4.比较的大小.
变式1.设,,中,则a,b,c的大小关系是( )
A. B. C. D.
变式2.已知,则,,的从大到小的顺序是______________.
考点五:求参数的范围
例5.若,求实数的取值范围.
变式1.已知,则的取值范围是( )
A. B. C. D.
变式2.已知幂函数过点,且,则实数k的取值范围是_____.
考点六:幂函数的应用
例6.(2015秋 西宁校级期中)已知幂函数在上单调递增,函数.
(1)求的值;
(2)当时,记的值域分别为集合,若,求实数的取值范围.
变式1. 设,已知函数在上是增函数.
(1)求函数的解析式;
(2)设,试讨论在上的单调性,并求在区间上的最值.
变式2.已知函数为偶函数,且.
(1)求函数的解析式;
(2)若在区间上为增函数,求实数的取值范围.
考点七:基本初等函数图象变换
例7.作出下列函数的图象:
(1) ; (2) ; (3) .
变式1:作出的图象.
变式2:作函数的图象.
巩固练习
1.幂函数的图象经过点,则_________.
2.函数的定义域为__________.
3.已知,,,则( )
A. B. C. D.
4.设,使为奇函数且在上单调递减的的值个数( ).
A. 1 B. 2 C. 3 D. 4
5.当时,下列函数的图象全在直线下方的偶函数是( ).
A. B. C. D.
6.如果是幂函数,则在其定义域上是( ).
A.增函数 B. 在上是增函数,在上是减函数
C.减函数 D.在上是减函数,在上也是减函数
7. 如图所示,幂函数在第一象限的图象,比较的大小( )
A.
B.
C.
D.
8. 三个数,,的大小顺序是( )
A.c
A. B. C. D.
10.如图曲线是幂函数在第一象限内的图象,已知取四个值,相应于曲线的依次为( )
11.下列命题中正确的是( )
幂函数的图象不经过点
幂函数的图象都经过点和点
若幂函数是奇函数,则是定义域上的增函数
幂函数的图象不可能出现在第四象限
12.函数的图象大致为( )
13.已知幂函数,若,则的取值范围是
14.幂函数在(0,+∞)上为增函数,则m=________.
15.(2015秋 湖南长沙期末)已知幂函数的图象关于轴对称,且在区间上是减函数,求函数的解析式.
16.已知幂函数的图象关于y轴对称,并且f(x)在第一象限是单调递减函数.
(1)求m的值;
(2)解不等式f(1-2x)≥f(2).
17.已知函数(m∈Z)是偶函数,且f(x)在(0,+∞)上单调递增.
(1)求m的值,并确定f(x)的解析式;
(2),求g(x)的定义域和值域.
18.已知幂函数在上是增函数,且在其定义域内是偶函数.
(1)求的值,并写出相应的函数
(2)对于(1)中求得的函数,设函数,问是否存在实数,使得在区间上是减函数,且在上是增函数,若存在,请求出来,若不存在,请说明理由。
4.4幂函数答案
典例解析
例1.
变式1:
变式2:A
例2.
变式1.C
变式2.B
例3:6432715
变式1:-1 2 1
变式2:D
例4:< <
变式1.C
变式2.
例5:
变式1.B
变式2.
例6:(1)0(2)
变式1:(1)(2)
变式2:(1)(2)
例7:略
变式1:略
变式2:略
巩固练习
1.
2.
3.A
4.A
5.B
6.D
7.D
8.B
9.B
10.A
11.D
12.C
13.
14.2
15:
16.(1)1(2)
17.(1)1 (2)
18.(1)1 (2)
8
9
