2021-2022学年数学人教B版(2019)选择性必修第一册2.7 抛物线(新课讲义)
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)选择性必修第一册2.7 抛物线(新课讲义) | 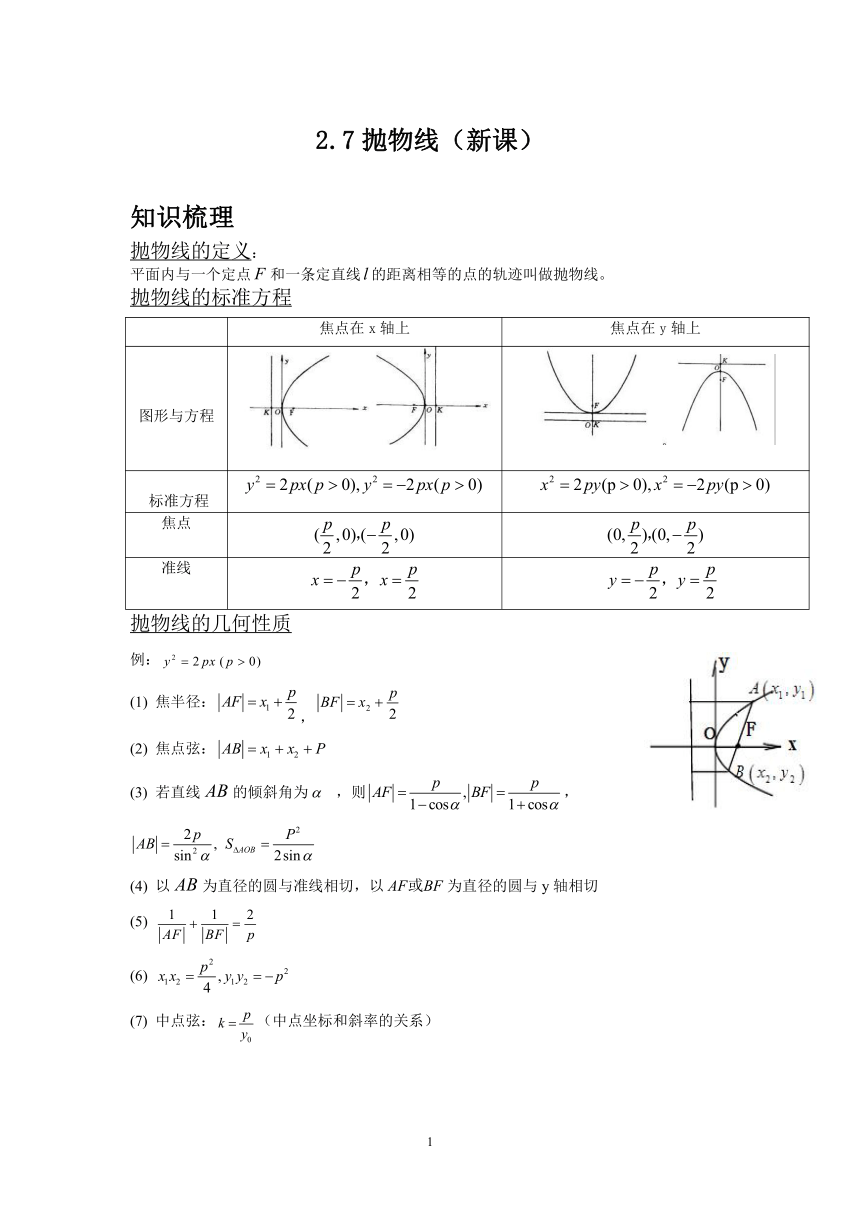 | |
| 格式 | doc | ||
| 文件大小 | 619.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 10:51:58 | ||
图片预览



文档简介
2.7抛物线(新课)
知识梳理
抛物线的定义:
平面内与一个定点和一条定直线的距离相等的点的轨迹叫做抛物线。
抛物线的标准方程
焦点在x轴上 焦点在y轴上
图形与方程
标准方程
焦点
准线
抛物线的几何性质
例:
(1) 焦半径:,
(2) 焦点弦:
(3) 若直线的倾斜角为,则,
(4) 以为直径的圆与准线相切,以为直径的圆与y轴相切
(5)
(6)
(7) 中点弦:(中点坐标和斜率的关系)
典例解析
考点一:抛物线的定义
例1.已知点P为抛物线y2 = 4x上动点,点Q(2,-1),求点P到Q点的距离与到抛物线焦点距离之和的最小值.
变式1.已知抛物线的焦点是,点是抛物线上的动点,又有点,的最小值____
变式2.设抛物线的焦点为,准线为,为抛物线上一点,,为垂足,如果直线的斜率为,那么等于____________。
考点二:抛物线的标准方程
例2.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:
(1)过点;
(2)焦点在直线:上 ( http: / / www. / wxc / )
变式1.分别求满足下列条件的抛物线的标准方程.
(1)焦点为;
(2)准线为 ;
(3)焦点到原点的距离为;
(4)过点;
(5)焦点在直线上.
变式2.已知抛物线的顶点在原点,焦点在轴负半轴上,过顶点且倾角为的弦长为,求抛物线的方程.
考点三:与抛物线有关的轨迹问题
例3. 若动圆与定圆:相外切,且与直线相切,求动圆圆心的轨迹方程.
变式1.平面上动点到定点的距离比到轴的距离大,求动点的轨迹方程。
变式2.若点到定点的距离比它到直线的距离小,求点的轨迹方程。
考点四:焦点弦
例4:(2014·新课标全国卷Ⅱ高考文科数学·T10) (2014·新课标全国卷Ⅱ高考文科数学·T10)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,则 = ( )
A. B.6 C.12 D.
变式1已知过抛物线的焦点的直线与抛物线相交于两点,若线段的中点 的横坐标为3,则线段的长度为( )
A、6 B、8 C、10 D、12
变式2.过抛物线的焦点作倾斜角为的直线交抛物线于两点,若线段的长为8,则______
例5.设抛物线的焦点为,过点作直线交抛物线于两点,若=3,则= .
变式1.已知以为焦点的抛物线上的两点满足,则弦的中点到准线的距离为
变式2.如图,过抛物线的焦点F的直线交抛物线于点A,B,交其准线l于点C.若,且,则此抛物线的方程为( )
A. B. C. D.
类型五:抛物线的综合
例6. 已知双曲线 的一条渐近线过点 ,且双曲线的一个焦点在抛
物线 的准线上,则双曲线的方程为( )
A. B. C. D.
变式1:(2015新课标全国卷I,文5)已知椭圆E的中心为坐标原点,离心率为,E的右焦点与抛物线的焦点重合,是C的准线与E的两个交点,则 ( )
A. B. C. D.
变式2.为抛物线上的动点,为圆: 上的动点,求的最小值.
巩固练习
1、已知抛物线关于轴对称,它的顶点在坐标原点,并且经过点。若点到该抛物线焦点的距离为,则( )
A、 B、 C、 D、
2. 若动点到点的距离与它到直线的距离相等,则点的轨迹方程__________.
3、在直角坐标系中,直线过抛物线的焦点,且与该抛物线相交于两点,其中点在轴上方,若直线的倾斜角为,则的面积为_______.
4、与圆外切且与y轴相切的动圆的圆心的轨迹方程是
5.(2009宁夏)已知抛物线的顶点在坐标原点,焦点为,直线l与抛物线相交于两点。若的中点为,则直线的方程为________.
6. 点到直线的距离与它到点距离之差为,求点的轨迹方程.
7、已知点F是抛物线的焦点,M是抛物线上的动点,当最小时,求M点坐标.
8、分别求满足下列条件的抛物线的标准方程.
(1)焦点为; (2)准线为 ;
(3)焦点到原点的距离为; (4)过点;
(5)焦点在直线上.
9、求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:
(1)过点;
(2)焦点在直线:上 ( http: / / www. / wxc / )
10、已知抛物线:过点.求抛物线的方程,并求其焦点坐标和准线方程.
11.分别求适合下列条件的抛物线方程.
(1)顶点在原点,以坐标轴为对称轴,且过点;
(2)顶点在原点,以坐标轴为对称轴,焦点到准线的距离为.
12. 已知抛物线的顶点在原点,对称轴是轴,抛物线上的点到焦点的距离等于,求抛物线的方程与的值.
2.7抛物线答案
典例解析:
例1: 3
变式1:
变式2: 8
例2:(1)所求的抛物线的方程为或,对应的准线方程分别是,.
(2)所求的抛物线的方程为或,对应的准线方程分别是,.
变式1:(1)所求抛物线的方程为;
(2)所求抛物线的标准方程为;
(3)所求抛物线的方程或;
(4)所求抛物线的方程为或;
(5)所求抛物线的标准方程为或.
变式2.抛物线方程为.
变式3.
例3. ,
变式1. 或。
变式2.动点的轨迹方程为。
例4: C
变式1. B
变式2. 2
例5.
变式1.
变式2.C
例6. D
变式1: B
变式2.
巩固练习
1、B
2.
3、
4、或
5.
6、
7、M(2,4)
8、(1)所求抛物线的方程为; (2)所求抛物线的标准方程为;
(3)所求抛物线的方程或;(4)所求抛物线的方程为或;
(5)所求抛物线的标准方程为或.
9、(1)所求的抛物线的方程为或,对应的准线方程分别是,.
(2)所求的抛物线的方程为或,对应的准线方程分别是,.
10、,焦点坐标为,准线方程为.
11.(1)或;
(2)或或或;
12.所以抛物线的方程为,
4
3
知识梳理
抛物线的定义:
平面内与一个定点和一条定直线的距离相等的点的轨迹叫做抛物线。
抛物线的标准方程
焦点在x轴上 焦点在y轴上
图形与方程
标准方程
焦点
准线
抛物线的几何性质
例:
(1) 焦半径:,
(2) 焦点弦:
(3) 若直线的倾斜角为,则,
(4) 以为直径的圆与准线相切,以为直径的圆与y轴相切
(5)
(6)
(7) 中点弦:(中点坐标和斜率的关系)
典例解析
考点一:抛物线的定义
例1.已知点P为抛物线y2 = 4x上动点,点Q(2,-1),求点P到Q点的距离与到抛物线焦点距离之和的最小值.
变式1.已知抛物线的焦点是,点是抛物线上的动点,又有点,的最小值____
变式2.设抛物线的焦点为,准线为,为抛物线上一点,,为垂足,如果直线的斜率为,那么等于____________。
考点二:抛物线的标准方程
例2.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:
(1)过点;
(2)焦点在直线:上 ( http: / / www. / wxc / )
变式1.分别求满足下列条件的抛物线的标准方程.
(1)焦点为;
(2)准线为 ;
(3)焦点到原点的距离为;
(4)过点;
(5)焦点在直线上.
变式2.已知抛物线的顶点在原点,焦点在轴负半轴上,过顶点且倾角为的弦长为,求抛物线的方程.
考点三:与抛物线有关的轨迹问题
例3. 若动圆与定圆:相外切,且与直线相切,求动圆圆心的轨迹方程.
变式1.平面上动点到定点的距离比到轴的距离大,求动点的轨迹方程。
变式2.若点到定点的距离比它到直线的距离小,求点的轨迹方程。
考点四:焦点弦
例4:(2014·新课标全国卷Ⅱ高考文科数学·T10) (2014·新课标全国卷Ⅱ高考文科数学·T10)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,则 = ( )
A. B.6 C.12 D.
变式1已知过抛物线的焦点的直线与抛物线相交于两点,若线段的中点 的横坐标为3,则线段的长度为( )
A、6 B、8 C、10 D、12
变式2.过抛物线的焦点作倾斜角为的直线交抛物线于两点,若线段的长为8,则______
例5.设抛物线的焦点为,过点作直线交抛物线于两点,若=3,则= .
变式1.已知以为焦点的抛物线上的两点满足,则弦的中点到准线的距离为
变式2.如图,过抛物线的焦点F的直线交抛物线于点A,B,交其准线l于点C.若,且,则此抛物线的方程为( )
A. B. C. D.
类型五:抛物线的综合
例6. 已知双曲线 的一条渐近线过点 ,且双曲线的一个焦点在抛
物线 的准线上,则双曲线的方程为( )
A. B. C. D.
变式1:(2015新课标全国卷I,文5)已知椭圆E的中心为坐标原点,离心率为,E的右焦点与抛物线的焦点重合,是C的准线与E的两个交点,则 ( )
A. B. C. D.
变式2.为抛物线上的动点,为圆: 上的动点,求的最小值.
巩固练习
1、已知抛物线关于轴对称,它的顶点在坐标原点,并且经过点。若点到该抛物线焦点的距离为,则( )
A、 B、 C、 D、
2. 若动点到点的距离与它到直线的距离相等,则点的轨迹方程__________.
3、在直角坐标系中,直线过抛物线的焦点,且与该抛物线相交于两点,其中点在轴上方,若直线的倾斜角为,则的面积为_______.
4、与圆外切且与y轴相切的动圆的圆心的轨迹方程是
5.(2009宁夏)已知抛物线的顶点在坐标原点,焦点为,直线l与抛物线相交于两点。若的中点为,则直线的方程为________.
6. 点到直线的距离与它到点距离之差为,求点的轨迹方程.
7、已知点F是抛物线的焦点,M是抛物线上的动点,当最小时,求M点坐标.
8、分别求满足下列条件的抛物线的标准方程.
(1)焦点为; (2)准线为 ;
(3)焦点到原点的距离为; (4)过点;
(5)焦点在直线上.
9、求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:
(1)过点;
(2)焦点在直线:上 ( http: / / www. / wxc / )
10、已知抛物线:过点.求抛物线的方程,并求其焦点坐标和准线方程.
11.分别求适合下列条件的抛物线方程.
(1)顶点在原点,以坐标轴为对称轴,且过点;
(2)顶点在原点,以坐标轴为对称轴,焦点到准线的距离为.
12. 已知抛物线的顶点在原点,对称轴是轴,抛物线上的点到焦点的距离等于,求抛物线的方程与的值.
2.7抛物线答案
典例解析:
例1: 3
变式1:
变式2: 8
例2:(1)所求的抛物线的方程为或,对应的准线方程分别是,.
(2)所求的抛物线的方程为或,对应的准线方程分别是,.
变式1:(1)所求抛物线的方程为;
(2)所求抛物线的标准方程为;
(3)所求抛物线的方程或;
(4)所求抛物线的方程为或;
(5)所求抛物线的标准方程为或.
变式2.抛物线方程为.
变式3.
例3. ,
变式1. 或。
变式2.动点的轨迹方程为。
例4: C
变式1. B
变式2. 2
例5.
变式1.
变式2.C
例6. D
变式1: B
变式2.
巩固练习
1、B
2.
3、
4、或
5.
6、
7、M(2,4)
8、(1)所求抛物线的方程为; (2)所求抛物线的标准方程为;
(3)所求抛物线的方程或;(4)所求抛物线的方程为或;
(5)所求抛物线的标准方程为或.
9、(1)所求的抛物线的方程为或,对应的准线方程分别是,.
(2)所求的抛物线的方程为或,对应的准线方程分别是,.
10、,焦点坐标为,准线方程为.
11.(1)或;
(2)或或或;
12.所以抛物线的方程为,
4
3
