23.2.3 关于原点对称的点的坐标 同步导学案(含答案)
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 同步导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 05:49:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
23.2 中心对称
23.2.3 关于原点对称的点的坐标
学习目标:1.掌握两点关于原点对称时,横纵坐标的关系.
2.会在平面直角坐标系内作关于原点对称的图形.
3.进一步体会数形结合的思想.
重点:会在平面直角坐标系内作关于原点对称的图形.
难点:掌握两点关于原点对称时,横纵坐标的关系.
一、知识链接
1.下列各点分别在坐标平面的什么位置上?
A(3,2):_______________; B(0,-2)_____________;
C(-3,-2):_______________; D(-3,0):_______________; 2·1·c·n·j·y
E(-1.5,3.5):_______________; F(2,-3):_______________.www-2-1-cnjy-com
2.已知P(-3,2),你能说出P关于x轴对称点A的坐标和关于y轴对称点B的坐标吗?并想一想点A与点B的位置关系是怎么样的?2-1-c-n-j-y
二、要点探究
探究点1:关于原点对称的点的坐标
问题 如何确定平面直角坐标系中点A( 2,1 )关于原点对称的点A′坐标?
练一练:在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
A(4,0),B(0,-3),C(2,1), D(-1,2), E(-3,-2)
思考 关于原点对称的两个点的坐标之间有什么关系?
知识要点 关于原点对称的点的坐标关系特点:横坐标、纵坐标都互为相反数,即:点
P(a,b)关于原点对称的点的坐标为P′(-a,-b);点P(a,b)关于x轴对称的点的坐标为
P′(a,-b);点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
简记为:“关于谁,谁不变,关于原点都改变”.
典例精析
例1 已知点P(2a+b,-3a)与点P'(8,b+2)关于原点对称,求a, b的值.
方法总结:关于原点对称的两个点横、纵坐标分别互为相反数,解题时可以直接根据此性质列方程(组)求解.
变式题:已知点P(1-a,2a-3)关于原点的对称点在第一象限,求a的取值范围.
方法总结:解决此类题目,通常求出该点关于原点的对称点的坐标,然后根据其所在的象限列不等式组解答.
练习
1.完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
关于原点的对称点
探究点2:利用关于原点对称的点的坐标关系作图
例2 如图,利用关于原点对称的点的坐标特点,作出△ABC关于原点对称的图形.
( http: / / www.21cnjy.com )
方法归纳:作关于原点对称的图形的步骤:
(1) 写出图形顶点坐标;
(2) 写出图形顶点关于原点的对称点的坐标;
(3) 描点;
(4) 顺次连接;
(5) 下结论.
练一练:
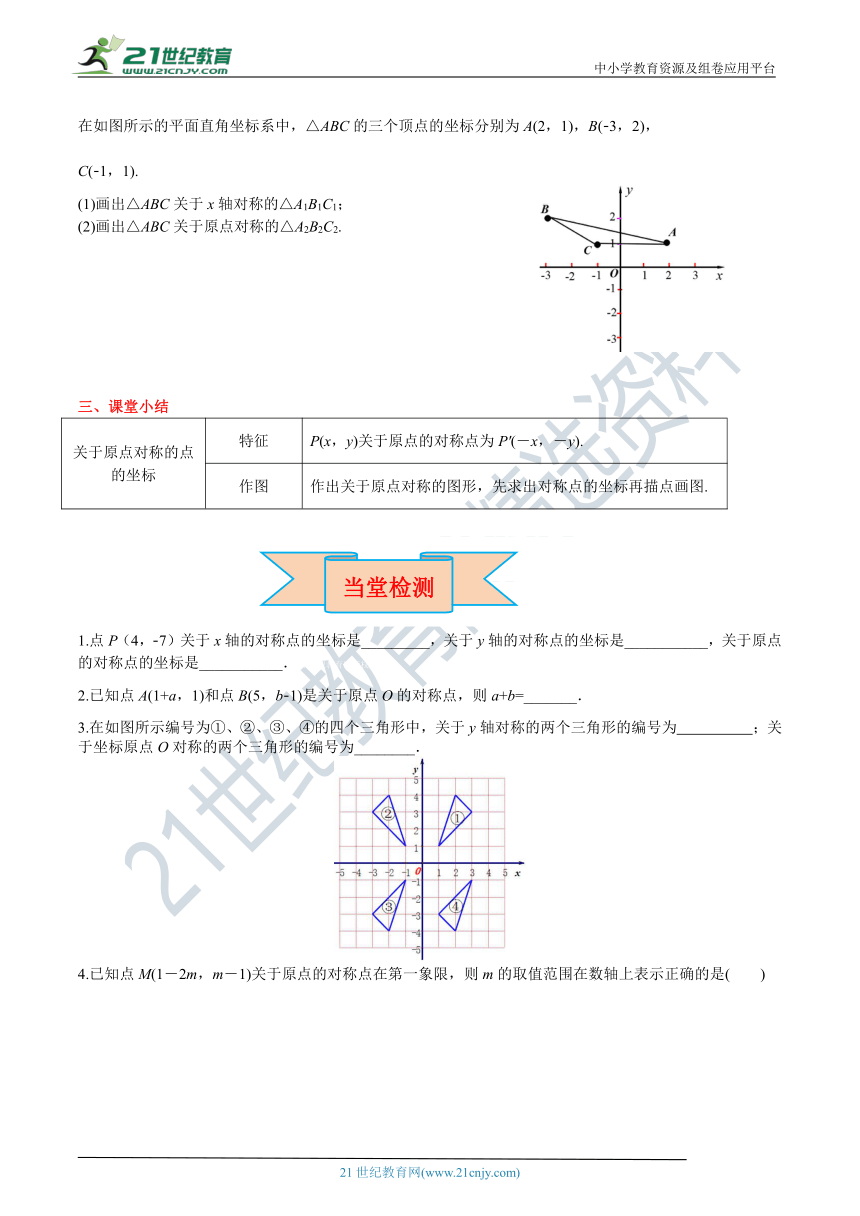
在如图所示的平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(-3,2),
C(-1,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC关于原点对称的△A2B2C2.
三、课堂小结
关于原点对称的点的坐标 特征 P(x,y)关于原点的对称点为P'(-x,-y).
作图 作出关于原点对称的图形,先求出对称点的坐标再描点画图.
1.点P(4,-7)关于x轴 ( http: / / www.21cnjy.com )的对称点的坐标是_________,关于y轴的对称点的坐标是___________,关于原点的对称点的坐标是___________.21世纪教育网版权所有
2.已知点A(1+a,1)和点B(5,b-1)是关于原点O的对称点,则a+b=_______.
3.在如图所示编号为①、② ( http: / / www.21cnjy.com )、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为________.21教育网
( http: / / www.21cnjy.com )
4.已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
( http: / / www.21cnjy.com )
5. (1)如图,在直角坐标系中,分 ( http: / / www.21cnjy.com )别描出点A,B,C关于原点O的对称点A1,B1,C1,写出点A1,B1,C1的坐标,并分别依次连接点A,B,C和点A1,B1,C1.www.21-cn-jy.com
(2)描述△ABC和△A1B1C1各对应顶点坐标之间的关系;
(3)△A1B1C1是由△ABC经怎样的变化得到的?
( http: / / www.21cnjy.com )
6.如图,阴影部分组成的图案,既是 ( http: / / www.21cnjy.com )关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),求点M 和点N 的坐标.21cnjy.com
( http: / / www.21cnjy.com )
参考答案
自主学习
1、知识链接
1. 第一象限 y轴上 第三象限 x轴上 第二象限 第四象限
2. 解:点A(-3,-2 ),点B(3,2);点A与点B关于原点O对称.
课堂探究
2、要点探究
: 探究点1:
问题 解:根据中心对 ( http: / / www.21cnjy.com )称的性质,对称点所连线段经过对称中心,而且被对称中心平分,可得OA=OA′,分别过点A、A′作x轴的垂线,构造直角三角形,利用全等可得出A′( -2,-1 ).【来源:21·世纪·教育·网】
练一练:解:A、B、C、D、E的对 ( http: / / www.21cnjy.com )称点分别为A′(-4,0),B′(0,3),C′(-2,-1),D′(1,-2),E′(3,2)(图略).21·世纪*教育网
思考 解:横坐标、纵坐标分别互为相反数.
典例精析
例1 解:由题意,得 解方程组,得
变式题:
解:点P关于原点的对称点P'的坐标为(a-1,3-2a).∵点P'在第一象限,∴
解得.
练习
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点 (2,3) (-1,-2) (-6,5) (0,1.6) (4,0)
关于y轴的对称点 (-2,-3) (1,2) (6,-5) (0,-1.6) (-4,0)
关于原点的对称点 (-2,3) (1,-2) (6,5) (0,1.6) (-4,0)
探究点2:
例2 图略
练一练 (1)图略 (2)图略
当堂检测
1. (4,7) (-4,-7) (-4,7) 2. -6 3. ①与② ①与③ 4. C21·cn·jy·com
5.(1)图略. (2)△ABC和△A1B1C1各对应顶点的横坐标互为相反数,纵坐标互为相反数.
(3)△A1B1C1是由△ABC绕着原点O旋转180°得到的.
6. M(-1,-3) N(1,-3)
自主学习
课堂探究
当堂检测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十三章 旋转
23.2 中心对称
23.2.3 关于原点对称的点的坐标
学习目标:1.掌握两点关于原点对称时,横纵坐标的关系.
2.会在平面直角坐标系内作关于原点对称的图形.
3.进一步体会数形结合的思想.
重点:会在平面直角坐标系内作关于原点对称的图形.
难点:掌握两点关于原点对称时,横纵坐标的关系.
一、知识链接
1.下列各点分别在坐标平面的什么位置上?
A(3,2):_______________; B(0,-2)_____________;
C(-3,-2):_______________; D(-3,0):_______________; 2·1·c·n·j·y
E(-1.5,3.5):_______________; F(2,-3):_______________.www-2-1-cnjy-com
2.已知P(-3,2),你能说出P关于x轴对称点A的坐标和关于y轴对称点B的坐标吗?并想一想点A与点B的位置关系是怎么样的?2-1-c-n-j-y
二、要点探究
探究点1:关于原点对称的点的坐标
问题 如何确定平面直角坐标系中点A( 2,1 )关于原点对称的点A′坐标?
练一练:在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
A(4,0),B(0,-3),C(2,1), D(-1,2), E(-3,-2)
思考 关于原点对称的两个点的坐标之间有什么关系?
知识要点 关于原点对称的点的坐标关系特点:横坐标、纵坐标都互为相反数,即:点
P(a,b)关于原点对称的点的坐标为P′(-a,-b);点P(a,b)关于x轴对称的点的坐标为
P′(a,-b);点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
简记为:“关于谁,谁不变,关于原点都改变”.
典例精析
例1 已知点P(2a+b,-3a)与点P'(8,b+2)关于原点对称,求a, b的值.
方法总结:关于原点对称的两个点横、纵坐标分别互为相反数,解题时可以直接根据此性质列方程(组)求解.
变式题:已知点P(1-a,2a-3)关于原点的对称点在第一象限,求a的取值范围.
方法总结:解决此类题目,通常求出该点关于原点的对称点的坐标,然后根据其所在的象限列不等式组解答.
练习
1.完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
关于原点的对称点
探究点2:利用关于原点对称的点的坐标关系作图
例2 如图,利用关于原点对称的点的坐标特点,作出△ABC关于原点对称的图形.
( http: / / www.21cnjy.com )
方法归纳:作关于原点对称的图形的步骤:
(1) 写出图形顶点坐标;
(2) 写出图形顶点关于原点的对称点的坐标;
(3) 描点;
(4) 顺次连接;
(5) 下结论.
练一练:
在如图所示的平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(-3,2),
C(-1,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC关于原点对称的△A2B2C2.
三、课堂小结
关于原点对称的点的坐标 特征 P(x,y)关于原点的对称点为P'(-x,-y).
作图 作出关于原点对称的图形,先求出对称点的坐标再描点画图.
1.点P(4,-7)关于x轴 ( http: / / www.21cnjy.com )的对称点的坐标是_________,关于y轴的对称点的坐标是___________,关于原点的对称点的坐标是___________.21世纪教育网版权所有
2.已知点A(1+a,1)和点B(5,b-1)是关于原点O的对称点,则a+b=_______.
3.在如图所示编号为①、② ( http: / / www.21cnjy.com )、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为________.21教育网
( http: / / www.21cnjy.com )
4.已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
( http: / / www.21cnjy.com )
5. (1)如图,在直角坐标系中,分 ( http: / / www.21cnjy.com )别描出点A,B,C关于原点O的对称点A1,B1,C1,写出点A1,B1,C1的坐标,并分别依次连接点A,B,C和点A1,B1,C1.www.21-cn-jy.com
(2)描述△ABC和△A1B1C1各对应顶点坐标之间的关系;
(3)△A1B1C1是由△ABC经怎样的变化得到的?
( http: / / www.21cnjy.com )
6.如图,阴影部分组成的图案,既是 ( http: / / www.21cnjy.com )关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),求点M 和点N 的坐标.21cnjy.com
( http: / / www.21cnjy.com )
参考答案
自主学习
1、知识链接
1. 第一象限 y轴上 第三象限 x轴上 第二象限 第四象限
2. 解:点A(-3,-2 ),点B(3,2);点A与点B关于原点O对称.
课堂探究
2、要点探究
: 探究点1:
问题 解:根据中心对 ( http: / / www.21cnjy.com )称的性质,对称点所连线段经过对称中心,而且被对称中心平分,可得OA=OA′,分别过点A、A′作x轴的垂线,构造直角三角形,利用全等可得出A′( -2,-1 ).【来源:21·世纪·教育·网】
练一练:解:A、B、C、D、E的对 ( http: / / www.21cnjy.com )称点分别为A′(-4,0),B′(0,3),C′(-2,-1),D′(1,-2),E′(3,2)(图略).21·世纪*教育网
思考 解:横坐标、纵坐标分别互为相反数.
典例精析
例1 解:由题意,得 解方程组,得
变式题:
解:点P关于原点的对称点P'的坐标为(a-1,3-2a).∵点P'在第一象限,∴
解得.
练习
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点 (2,3) (-1,-2) (-6,5) (0,1.6) (4,0)
关于y轴的对称点 (-2,-3) (1,2) (6,-5) (0,-1.6) (-4,0)
关于原点的对称点 (-2,3) (1,-2) (6,5) (0,1.6) (-4,0)
探究点2:
例2 图略
练一练 (1)图略 (2)图略
当堂检测
1. (4,7) (-4,-7) (-4,7) 2. -6 3. ①与② ①与③ 4. C21·cn·jy·com
5.(1)图略. (2)△ABC和△A1B1C1各对应顶点的横坐标互为相反数,纵坐标互为相反数.
(3)△A1B1C1是由△ABC绕着原点O旋转180°得到的.
6. M(-1,-3) N(1,-3)
自主学习
课堂探究
当堂检测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
