安徽省宿州市砀山重点高中2021-2022学年高二上学期第一次质量检测数学试题(Word版含答案)
文档属性
| 名称 | 安徽省宿州市砀山重点高中2021-2022学年高二上学期第一次质量检测数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 786.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 08:49:32 | ||
图片预览



文档简介
砀山中学2020级高二第一次质量检测
数学试卷
一、选择题
1. 角的终边所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 已知单位向量,满足,则向量与的夹角是
A.0 B. C. D.
3. 已知平面、和直线m、l,要使“若,,,则”正确,则须添加条件
A. B.
C. l与相交但不垂直 D. l与m为异面直线
4. 如图,在空间四边形中,设分别是,的中点,
则
A. B.
C. D.
5. 中国古代数学专著《九章算术》中对两类空间几何体有这样的记载:①“堑堵”,即底面为直角三角形,且侧棱垂直于底面的三棱柱;②“阳马”,即底面为矩形,且有一侧棱垂直于底面的四棱锥.现有一“堑堵”,如图所示,,则其中“阳马”与“堑堵”的体积之比为
A.1:2 B. 2:3
C.3:4 D. 4:5
6.已知函数部分图象大致如图所示,则的最小正周期为
A. B.
C. D.
7. 在空间直角坐标中,为坐标原点,若点在平面上的投影点为
,则线段的长度为
A. B. C. D.3
8.已知顶点在原点,始边在x轴非负半轴的锐角绕原点逆时针转后,终边交单位圆于,则的值为
A. B. C. D.
9.如图,在四棱锥中,底面,四边形为正方形,
且,为的重心,则与底面所成的角的正弦值等于
A. B. C. D.
10. 已知是球的球面上两点,,为该球面上的动点,若三棱锥
的体积的最大值为,则球的表面积为
A. B. C. D.
11.在正方体ABCD﹣A1B1C1D1中,过点C做直线l,使得直线l与直线BA1和B1D1所成的
角均为,则这样的直线l有
A.1条 B.2条 C.4条 D.无数条
已知棱长为的正方体,点在空间直角坐标系的轴上移动,
点在平面上移动,则的最大值是
A. B. C. D.
二、填空题
13. 已知两个平面,的法向量分别是和,若,则
.
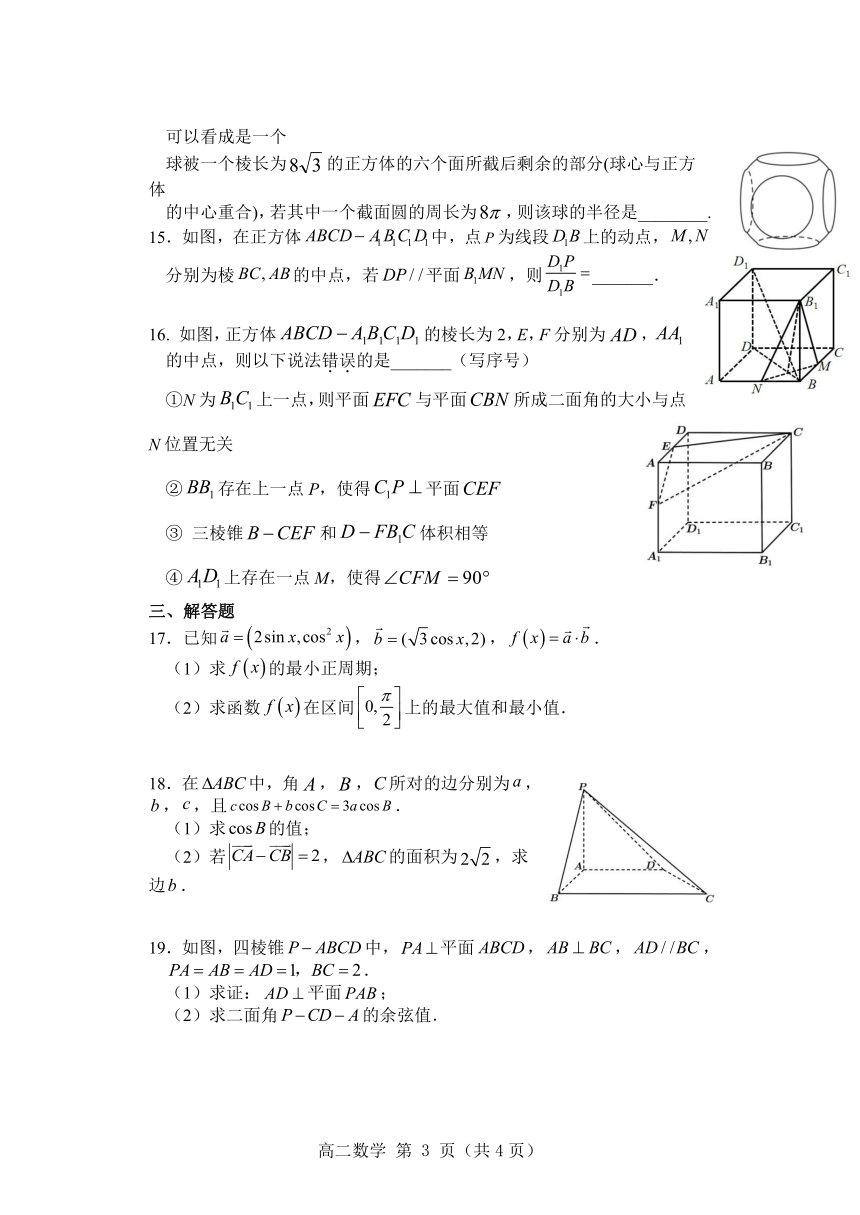
14.某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个
球被一个棱长为的正方体的六个面所截后剩余的部分(球心与正方体
的中心重合),若其中一个截面圆的周长为,则该球的半径是________.
15.如图,在正方体中,点为线段上的动点,
分别为棱的中点,若平面,则_______.
16. 如图,正方体的棱长为2,E,F分别为,的中点,则以下说法错误的是_______(写序号)
①N为上一点,则平面与平面所成二面角的大小与点N位置无关
②存在上一点P,使得平面
③ 三棱锥和体积相等
④上存在一点M,使得
三、解答题
17.已知,,.
(1)求的最小正周期;
(2)求函数在区间上的最大值和最小值.
18.在中,角,,所对的边分别为,,,且.
(1)求的值;
(2)若,的面积为,求边.
19.如图,四棱锥中,平面,,,.
(1)求证:平面;
(2)求二面角的余弦值.
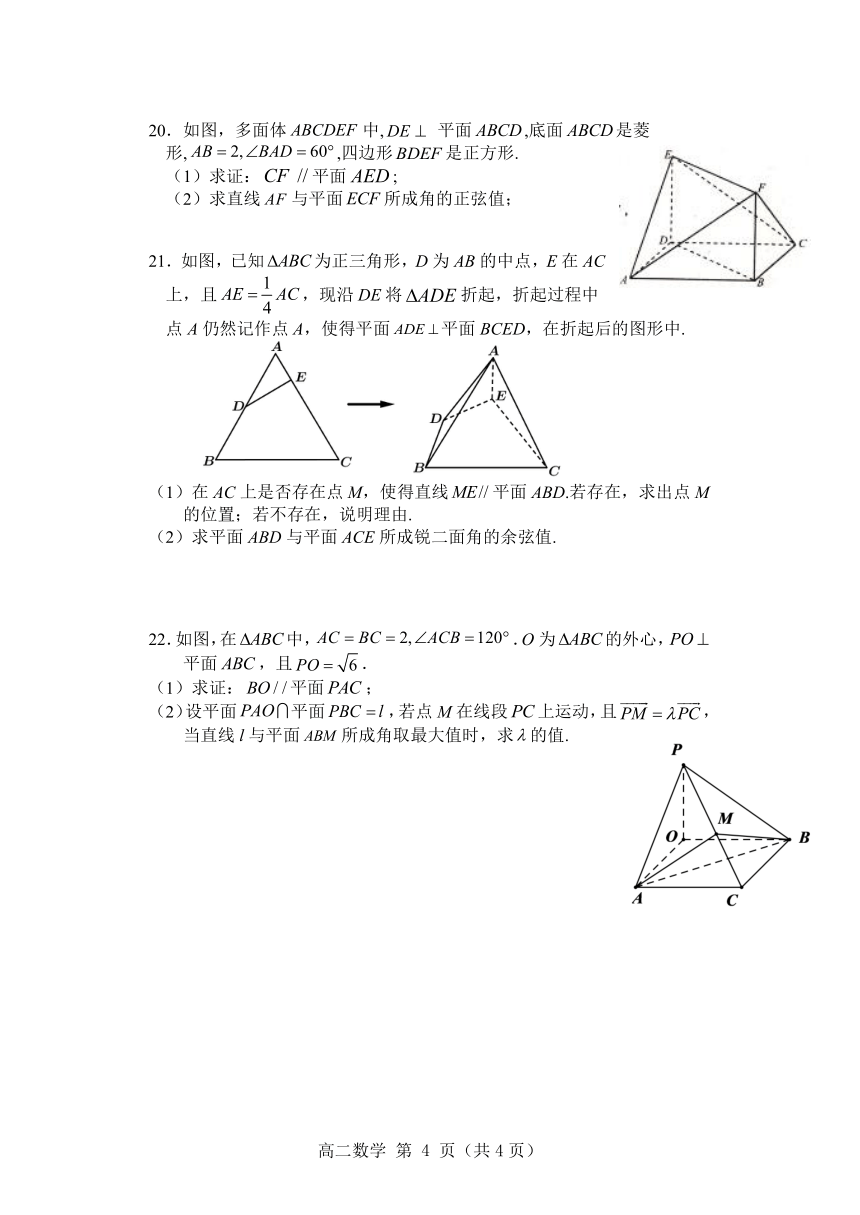
20.如图,多面体中, 平面,底面是菱形,,四边形是正方形.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
21.如图,已知为正三角形,D为AB的中点,E在AC上,且,现沿DE将折起,折起过程中点A仍然记作点A,使得平面平面BCED,在折起后的图形中.
(1)在AC上是否存在点M,使得直线平面ABD.若存在,求出点M的位置;若不存在,说明理由.
(2)求平面ABD与平面ACE所成锐二面角的余弦值.
22.如图,在中,.O为的外心,平面,且.
(1)求证:平面;
(2)设平面平面,若点M在线段上运动,且,当直线l与平面所成角取最大值时,求的值.
高二第一次月考数学答案
选择题
1-6 C A B C B A
7-12 A D C B C D
填空题
8, 8,,②
解答题
17.解:,,
由
,.............................................................3分
的最小正周期, .............................................................5分
由可得:
当时,函数取得最小值为 ..............................7分
当时,函数取得最大值为
故得函数在区间上的最大值为3,最小值为0...............................10分
18.解:在中,角,,所对的边分别为,,,且.
则:,
整理得:,
所以:;.............................................................6分
(2)由于,,
所以:,
在中,由于:,则:,即:.
由于的面积为,所以:,
解得:, .............................................................8分
故:,解得:................................12分
19.(1)∵平面,∴.
又,,∴
∵,∴平面; .............................................................5分
(2)
以A为原点,分别为x轴、y轴、z轴的正方向建立空间直角坐标系,则
.............................................................6分
显然为平面ABCD的一个法向量. .............................................................7分
设为平面PCD的一个法向量.,则:
,即不妨设y=1,则 .....................................................9分
设二面角的平面角为,由图示可知为锐角,
所以. ........................................11分
即二面角的余弦值为. .............................................................12分
20.解:(1)因为是菱形, 所以.又 平面平面 所以平面 又因为是正方形,所以 .因为平面平面所以平面因为平面平面,
所以平面平面 ,因为平面 ,
所以平面 . ............................................................5分
(2)因为四边形为菱形,且 ,所以为等边三角形,取 的中点,
所以,取 的中点,连结 ,则,
因为平面 ,所以平面 .
以为 轴、为 轴、为 轴建立空间直角坐标系........................6分
因为 .
所以..............................7分
所以设平面 法向量为
则有得 令.则 ....................................9分
设与平面 所成的角为,
则............................................................11分
所以直线 与所成角的正弦值为 .............................................................12分
21.(1)当时,平面.
证明如下:在BC上取点H,使得,则,,
又平面,平面,,平面ABD,
平面ABD,,
∴平面平面ABD,又平面EMH,
∴平面ABD. .............................................................5分
(2)在ADE中,∵,,∴.
又平面平面BCED,平面平面,平面ADE,
∴平面BCED.
以E为原点,以ED,EC,EA为坐标轴建立空间直角坐标系,如图所示:.................6分
设正三角形ABC的边长为4,则,,,,
∴,,
设平面ABD的法向量为,则,
∴,令得..............................................................8分
又平面ACE,∴为平面ACE的一个法向量.....................................9分
∴..............................................................11分
∴平面ABD与平面ACE所成锐二面角的余弦值为........................................12分
22.(1)如图,连接,交于点D,O为的外心,
,所以,
所以
故和都为等边三角形,
即四边形为菱形,所以
又平面,平面,所以平面................................5分
(2)由(1)同理可知因为平面,平面,
平面平面,所以.
如图所示:以点D为原点,和垂直平面的直线分别为x,y,z轴建立空间直角坐标系.
则....................................6分
设所以
设平面的法向量为.
,
得,
令得..............................................................8分
所以直线l与平面所成角的正弦值为:
,
即当即点M是线段的中点时,直线l与平面所成角取最大值..............................................................12分
数学试卷
一、选择题
1. 角的终边所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 已知单位向量,满足,则向量与的夹角是
A.0 B. C. D.
3. 已知平面、和直线m、l,要使“若,,,则”正确,则须添加条件
A. B.
C. l与相交但不垂直 D. l与m为异面直线
4. 如图,在空间四边形中,设分别是,的中点,
则
A. B.
C. D.
5. 中国古代数学专著《九章算术》中对两类空间几何体有这样的记载:①“堑堵”,即底面为直角三角形,且侧棱垂直于底面的三棱柱;②“阳马”,即底面为矩形,且有一侧棱垂直于底面的四棱锥.现有一“堑堵”,如图所示,,则其中“阳马”与“堑堵”的体积之比为
A.1:2 B. 2:3
C.3:4 D. 4:5
6.已知函数部分图象大致如图所示,则的最小正周期为
A. B.
C. D.
7. 在空间直角坐标中,为坐标原点,若点在平面上的投影点为
,则线段的长度为
A. B. C. D.3
8.已知顶点在原点,始边在x轴非负半轴的锐角绕原点逆时针转后,终边交单位圆于,则的值为
A. B. C. D.
9.如图,在四棱锥中,底面,四边形为正方形,
且,为的重心,则与底面所成的角的正弦值等于
A. B. C. D.
10. 已知是球的球面上两点,,为该球面上的动点,若三棱锥
的体积的最大值为,则球的表面积为
A. B. C. D.
11.在正方体ABCD﹣A1B1C1D1中,过点C做直线l,使得直线l与直线BA1和B1D1所成的
角均为,则这样的直线l有
A.1条 B.2条 C.4条 D.无数条
已知棱长为的正方体,点在空间直角坐标系的轴上移动,
点在平面上移动,则的最大值是
A. B. C. D.
二、填空题
13. 已知两个平面,的法向量分别是和,若,则
.
14.某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个
球被一个棱长为的正方体的六个面所截后剩余的部分(球心与正方体
的中心重合),若其中一个截面圆的周长为,则该球的半径是________.
15.如图,在正方体中,点为线段上的动点,
分别为棱的中点,若平面,则_______.
16. 如图,正方体的棱长为2,E,F分别为,的中点,则以下说法错误的是_______(写序号)
①N为上一点,则平面与平面所成二面角的大小与点N位置无关
②存在上一点P,使得平面
③ 三棱锥和体积相等
④上存在一点M,使得
三、解答题
17.已知,,.
(1)求的最小正周期;
(2)求函数在区间上的最大值和最小值.
18.在中,角,,所对的边分别为,,,且.
(1)求的值;
(2)若,的面积为,求边.
19.如图,四棱锥中,平面,,,.
(1)求证:平面;
(2)求二面角的余弦值.
20.如图,多面体中, 平面,底面是菱形,,四边形是正方形.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
21.如图,已知为正三角形,D为AB的中点,E在AC上,且,现沿DE将折起,折起过程中点A仍然记作点A,使得平面平面BCED,在折起后的图形中.
(1)在AC上是否存在点M,使得直线平面ABD.若存在,求出点M的位置;若不存在,说明理由.
(2)求平面ABD与平面ACE所成锐二面角的余弦值.
22.如图,在中,.O为的外心,平面,且.
(1)求证:平面;
(2)设平面平面,若点M在线段上运动,且,当直线l与平面所成角取最大值时,求的值.
高二第一次月考数学答案
选择题
1-6 C A B C B A
7-12 A D C B C D
填空题
8, 8,,②
解答题
17.解:,,
由
,.............................................................3分
的最小正周期, .............................................................5分
由可得:
当时,函数取得最小值为 ..............................7分
当时,函数取得最大值为
故得函数在区间上的最大值为3,最小值为0...............................10分
18.解:在中,角,,所对的边分别为,,,且.
则:,
整理得:,
所以:;.............................................................6分
(2)由于,,
所以:,
在中,由于:,则:,即:.
由于的面积为,所以:,
解得:, .............................................................8分
故:,解得:................................12分
19.(1)∵平面,∴.
又,,∴
∵,∴平面; .............................................................5分
(2)
以A为原点,分别为x轴、y轴、z轴的正方向建立空间直角坐标系,则
.............................................................6分
显然为平面ABCD的一个法向量. .............................................................7分
设为平面PCD的一个法向量.,则:
,即不妨设y=1,则 .....................................................9分
设二面角的平面角为,由图示可知为锐角,
所以. ........................................11分
即二面角的余弦值为. .............................................................12分
20.解:(1)因为是菱形, 所以.又 平面平面 所以平面 又因为是正方形,所以 .因为平面平面所以平面因为平面平面,
所以平面平面 ,因为平面 ,
所以平面 . ............................................................5分
(2)因为四边形为菱形,且 ,所以为等边三角形,取 的中点,
所以,取 的中点,连结 ,则,
因为平面 ,所以平面 .
以为 轴、为 轴、为 轴建立空间直角坐标系........................6分
因为 .
所以..............................7分
所以设平面 法向量为
则有得 令.则 ....................................9分
设与平面 所成的角为,
则............................................................11分
所以直线 与所成角的正弦值为 .............................................................12分
21.(1)当时,平面.
证明如下:在BC上取点H,使得,则,,
又平面,平面,,平面ABD,
平面ABD,,
∴平面平面ABD,又平面EMH,
∴平面ABD. .............................................................5分
(2)在ADE中,∵,,∴.
又平面平面BCED,平面平面,平面ADE,
∴平面BCED.
以E为原点,以ED,EC,EA为坐标轴建立空间直角坐标系,如图所示:.................6分
设正三角形ABC的边长为4,则,,,,
∴,,
设平面ABD的法向量为,则,
∴,令得..............................................................8分
又平面ACE,∴为平面ACE的一个法向量.....................................9分
∴..............................................................11分
∴平面ABD与平面ACE所成锐二面角的余弦值为........................................12分
22.(1)如图,连接,交于点D,O为的外心,
,所以,
所以
故和都为等边三角形,
即四边形为菱形,所以
又平面,平面,所以平面................................5分
(2)由(1)同理可知因为平面,平面,
平面平面,所以.
如图所示:以点D为原点,和垂直平面的直线分别为x,y,z轴建立空间直角坐标系.
则....................................6分
设所以
设平面的法向量为.
,
得,
令得..............................................................8分
所以直线l与平面所成角的正弦值为:
,
即当即点M是线段的中点时,直线l与平面所成角取最大值..............................................................12分
同课章节目录
