4.5 牛顿运动定律的应用 —【新教材】粤教版(2019)高中物理必修一课件(共15张PPT)
文档属性
| 名称 | 4.5 牛顿运动定律的应用 —【新教材】粤教版(2019)高中物理必修一课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 439.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-12 08:57:36 | ||
图片预览




文档简介
(共15张PPT)
4.5 牛顿运动定律的应用
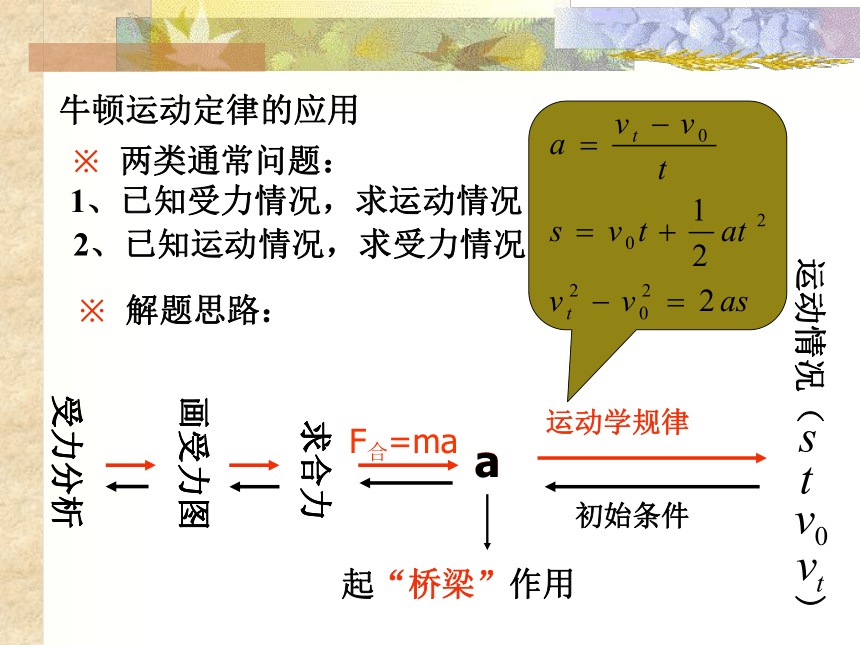
牛顿运动定律的应用
※ 两类通常问题:
1、已知受力情况,求运动情况
受力分析
画受力图
求合力
a
F合=ma
运动学规律
初始条件
※ 解题思路:
运动情况( )
a
起“桥梁”作用
2、已知运动情况,求受力情况
求合力
画受力图
受力分析
课本P117例1
解:火车的运动情况和受力情况如图所示。
t=1min20s
=72km/h
选取火车前进方向为正方向,
=20m/s
=80s
=6.0 ×105kg
mg
FN
F
f
由牛顿第二定律F合=ma,得
火车所受合外力为
F合=6.0×105 ×0.25N=1.5×105 N
即火车在加速过程中的合外力约为1.5 ×105 N才能满足加速的要求。
实际情况中,火车肯定受阻力的影响。设火车受到
的阻力是车重的0.05倍,这时火车的牵引力是多大?
F合=F牵-f,
f=0.05mg=3.0×105N
F牵=F合+f=4.5×105 N
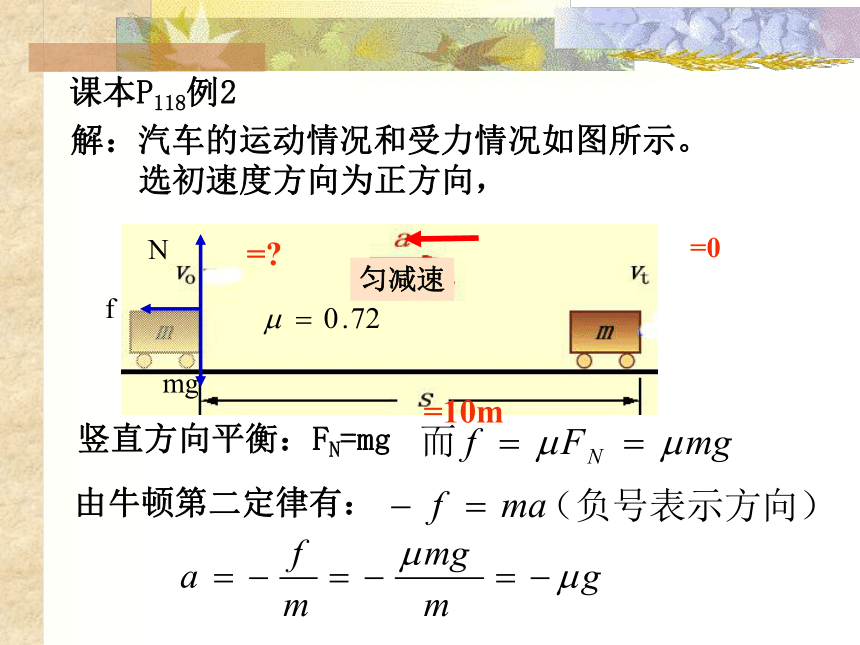
课本P118例2
解:汽车的运动情况和受力情况如图所示。
mg
N
f
=10m
=0
=
竖直方向平衡:FN=mg
由牛顿第二定律有:
选初速度方向为正方向,
匀减速
即汽车刹车前速度为43.2km/h,此汽车属超速行驶。
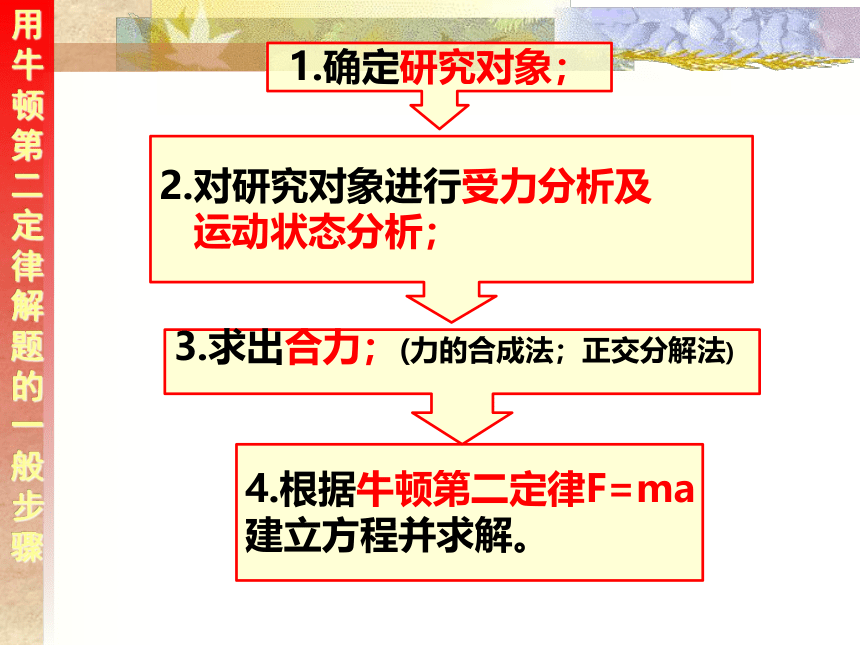
用牛顿第二定律解题的一般步骤
1.确定研究对象;
2.对研究对象进行受力分析及
运动状态分析;
3.求出合力;(力的合成法;正交分解法)
4.根据牛顿第二定律F=ma
建立方程并求解。
练习:1、 一木箱质量为m,与水平地面间的动摩擦因数为μ,现用斜向右下方与水平方向成θ角的力F推木箱,求经过 t 秒时木箱的加速度。
G
N
f
θ
Vt=?
V0= 0
F
Fcosθ
Fsinθ
竖直方向 N– Fsinθ- G = 0 ①
水平方向 Fcosθ- f = ma ②
二者联系 f=μN ③
如果还要求经过 t 秒时木箱的速度vt=a t
2、光滑的水平面上有质量分别为m1、m2的两物体 静止靠在一起(如图) ,现对m1施加一个大小为 F 方向向右的推力作用。求此时物体m2受到物体 m1的作用力F1
m1
m2
F
[m1]
F
F1
[m2]
F1
FN1
[ 解法一 ]:
分别以m1、m2为隔离体作受力分析
FN2
m1g
m2g
对m1有 :F – F1 = m 1a (1)
对m2有: F1 = m2 a (2)
联立(1)、(2)可得
F1 =
m1
m2
F
[m2]
F1
FN2
[ 解法二 ]:
对m1、m2视为整体作受力分析
m2g
有 :F = (m 1+ m2)a (1)
对m2作受力分析
联立(1)、(2)可得
F1 =
FN
(m1 + m2)g
F
有 :F1 = m2 a (2)
2、光滑的水平面上有质量分别为m1、m2的两物体 静止靠在一起(如图) ,现对m1施加一个大小为 F 方向向右的推力作用。求此时物体m2受到物体 m1的作用力F1
求m1对m2的作用力大小。
m1 m2
m2g
F1
FN
Ff
用水平推力F向左推 m1、m2间的作用力与原来相同吗?
对m2受力分析:
4.5 牛顿运动定律的应用
牛顿运动定律的应用
※ 两类通常问题:
1、已知受力情况,求运动情况
受力分析
画受力图
求合力
a
F合=ma
运动学规律
初始条件
※ 解题思路:
运动情况( )
a
起“桥梁”作用
2、已知运动情况,求受力情况
求合力
画受力图
受力分析
课本P117例1
解:火车的运动情况和受力情况如图所示。
t=1min20s
=72km/h
选取火车前进方向为正方向,
=20m/s
=80s
=6.0 ×105kg
mg
FN
F
f
由牛顿第二定律F合=ma,得
火车所受合外力为
F合=6.0×105 ×0.25N=1.5×105 N
即火车在加速过程中的合外力约为1.5 ×105 N才能满足加速的要求。
实际情况中,火车肯定受阻力的影响。设火车受到
的阻力是车重的0.05倍,这时火车的牵引力是多大?
F合=F牵-f,
f=0.05mg=3.0×105N
F牵=F合+f=4.5×105 N
课本P118例2
解:汽车的运动情况和受力情况如图所示。
mg
N
f
=10m
=0
=
竖直方向平衡:FN=mg
由牛顿第二定律有:
选初速度方向为正方向,
匀减速
即汽车刹车前速度为43.2km/h,此汽车属超速行驶。
用牛顿第二定律解题的一般步骤
1.确定研究对象;
2.对研究对象进行受力分析及
运动状态分析;
3.求出合力;(力的合成法;正交分解法)
4.根据牛顿第二定律F=ma
建立方程并求解。
练习:1、 一木箱质量为m,与水平地面间的动摩擦因数为μ,现用斜向右下方与水平方向成θ角的力F推木箱,求经过 t 秒时木箱的加速度。
G
N
f
θ
Vt=?
V0= 0
F
Fcosθ
Fsinθ
竖直方向 N– Fsinθ- G = 0 ①
水平方向 Fcosθ- f = ma ②
二者联系 f=μN ③
如果还要求经过 t 秒时木箱的速度vt=a t
2、光滑的水平面上有质量分别为m1、m2的两物体 静止靠在一起(如图) ,现对m1施加一个大小为 F 方向向右的推力作用。求此时物体m2受到物体 m1的作用力F1
m1
m2
F
[m1]
F
F1
[m2]
F1
FN1
[ 解法一 ]:
分别以m1、m2为隔离体作受力分析
FN2
m1g
m2g
对m1有 :F – F1 = m 1a (1)
对m2有: F1 = m2 a (2)
联立(1)、(2)可得
F1 =
m1
m2
F
[m2]
F1
FN2
[ 解法二 ]:
对m1、m2视为整体作受力分析
m2g
有 :F = (m 1+ m2)a (1)
对m2作受力分析
联立(1)、(2)可得
F1 =
FN
(m1 + m2)g
F
有 :F1 = m2 a (2)
2、光滑的水平面上有质量分别为m1、m2的两物体 静止靠在一起(如图) ,现对m1施加一个大小为 F 方向向右的推力作用。求此时物体m2受到物体 m1的作用力F1
求m1对m2的作用力大小。
m1 m2
m2g
F1
FN
Ff
用水平推力F向左推 m1、m2间的作用力与原来相同吗?
对m2受力分析:
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
