2021—2022学年 北师大版数学九年级上册2.6应用一元二次方程 课件(共2课时 22张)
文档属性
| 名称 | 2021—2022学年 北师大版数学九年级上册2.6应用一元二次方程 课件(共2课时 22张) |  | |
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 10:55:47 | ||
图片预览







文档简介
(共22张PPT)
2.6 应用一元二次方程
第1课时 几何动点问题与图形面积
创设情境 温故探新
复习
导入
还记得本章开始时梯子下滑的问题吗?
①在这个问题中,梯子顶端下滑1米时,梯子底端滑动的距离大于1米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?呢?
②如果梯子长度是13米,梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
合作交流探究新知
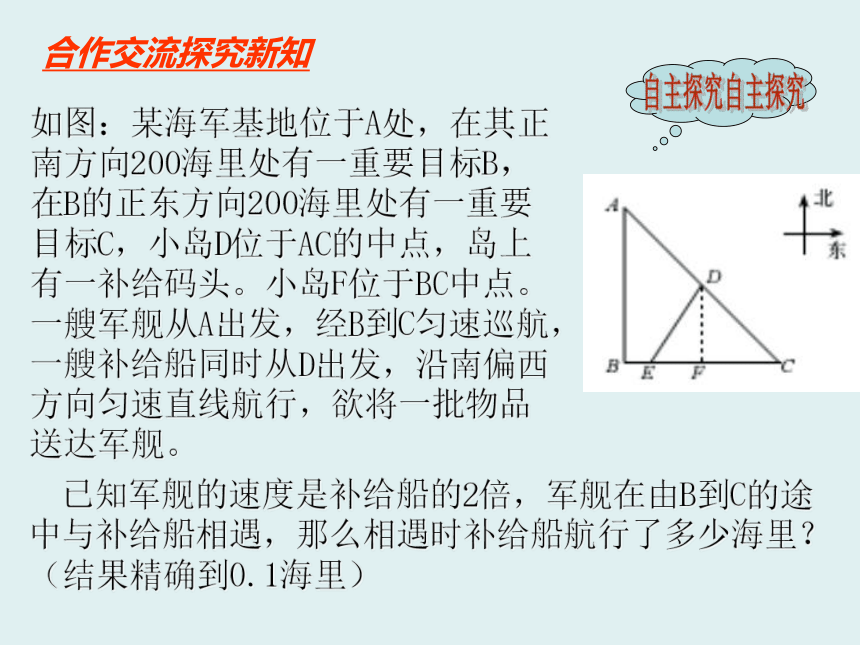
如图:某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头。小岛F位于BC中点。一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰。
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
合作交流探究新知
(1)要求DE的长,需要如何设未知数?
(2)怎样建立含DE未知数的等量关系?从已知条件中能找到吗?
(3)利用勾股定理建立等量关系,如何构造直角三角形?
(4)选定Rt△DEF后,三条边长都是已知的吗?DE,DF,EF分别是多少?
合作交流探究新知
速度等量:V军舰=2×V补给船
时间等量:t军舰=t补给船
三边数量关系:EF2+FD2=DE2
例1:
范例研讨运用新知
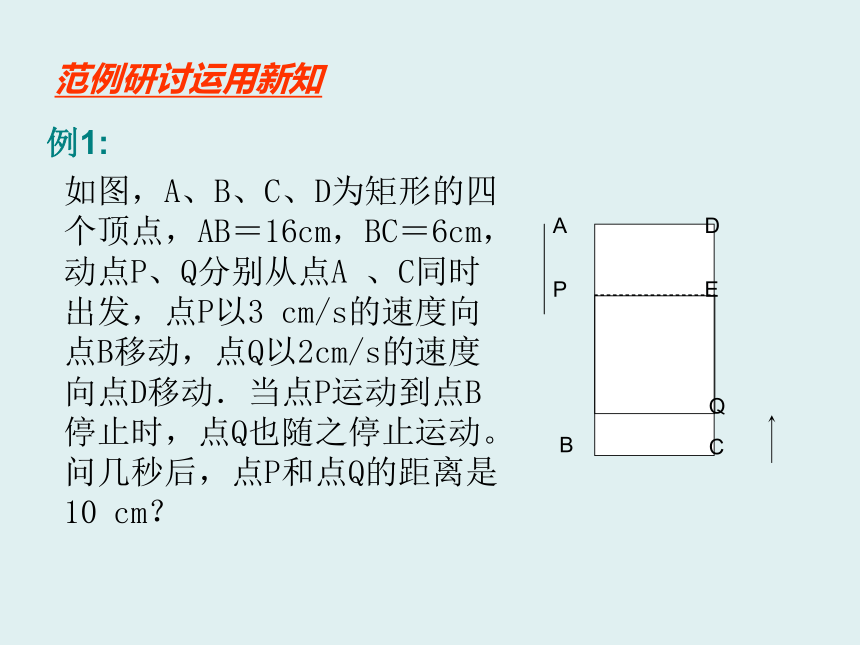
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A 、C同时出发,点P以3 cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动。问几秒后,点P和点Q的距离是10 cm?
A
B
C
D
P
Q
E
范例研讨运用新知
解:设t秒后,点P和点Q的距离是10 cm,则AP=3t,CQ=2t
过点P作PE⊥CD于E
所以四边形APDE是矩形,所以AD=PE=6cm
EQ=16-2t-3t=16-5t
在直角三角形PQE中,PQ2=PE2+EQ2
100=62+(16-5t)2
解这个方程,得,
答:秒或秒后,点P和点Q的距离是10 cm
反馈练习巩固新知
1. 一架长为10米的梯子斜靠在墙
上,梯子的顶端距地面的垂直距
离为6米,如果梯子的顶端沿墙
壁下滑1米,那么梯子的底端向后滑动的距( )
A 等于1米 B 大于1米 C 小于1米 D 不能确定
2.某生活小区准备在每幢楼房之间,开辟面积为200平方米的一块长方形绿地,并且长比宽多10米,则绿地的长为_____米,宽为_______米;
反馈练习巩固新知
3.下图是中北居民小区某一休闲场所
的平面示意图.图中阴影部分是草
坪和健身器材安装区,空白部分是用做散步的道路.东西方向的一条主干道较宽,
其余道路的宽度相等,主干道的
宽度是其余道路的宽度的2倍.
这块休闲场所南北长18m,东西宽
16m.已知这休闲场地中草坪和健
身器材安装区的面积为168m2,
请问主干道的宽度为多少米?
北
西
东
课堂小结布置作业
小结:
列方程解应用题的一般步骤:
(1)审题.了解问题的实际意义,分清已知条件和未知量之间的关系.
(2)设未知数.一般情况下求什么设什么为未知数.
(3)列方程.根据量与量之间的关系,找出相等关系,列出方程.
(4)解方程.灵活运用一元二次方程的四种解法.
(5)验根.检验一元二次方程的根是否满足题意.
(6)答.作答.
课堂小结布置作业
作业:
如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动。能使△PBQ的面积为15cm2 的是多少秒?
B
A
C
P
Q
2.6 应用一元二次方程
第2课时 利润与变化率
创设情境 温故探新
复习
导入
请同学们回忆并回答与利润相关的知识
利润率=________
利润=_____-进价
售价=标价×折扣
9折要乘以90%或0.9或 ,
那么x折呢?
合作交流探究新知
例2:
新华商场销售某种冰箱,每台进货价为
2500元。市场调研表明:当销售价为2900元时,
平均每天能售出8台;而当销售价每降低50元时,
平均每天就能多售出4台。商场要想使这种冰箱
的销售利润平均每天达到5000元,每台冰箱的
降价应为多少元?
合作交流探究新知
(1)要求每台冰箱的定价应为多少元,
需要如何设未知数?
(2)降价后每台冰箱的利润是多少?
(3)降价后卖出冰箱的台数?
本题的主要等量关系:
每台冰箱的销售利润×平均每天的销售台数=5000
范例研讨运用新知
将进货单价为40元的商品按50元售出时,就能卖出500个.已知这种商品每个涨价1元,其销售量就减少10个,问为了赚得8000元的利润,售价应定为多少?这时应进货多少个?
范例研讨运用新知
解:设商品的单价是(50+x)元,则每个商品的利润是[(50+x)-40]元,销售量是(500-10x)个.
[(50+x)-40](500-10x)=8000
x2-40x+300=0
x1=10,x2=30
故商品的的单价可定为50+10=60元或50+30=80元.
当单价为60元时,其进货量只能是500-10×10=400个;
当单价为80元时,其进货量只能是500-10×30=200个.
答:为了赚得8000元的利润,售价应定为60元,这时应进货多400个或定为80元,这时应进货200个.
反馈练习巩固新知
1.裕丰商店一月份的利润为50万元,二、三月份的利润平均增长率为m,下列各式中,正确表示这个商店第一季度的总利润的是( )
A.50[m2+3m+3] 万元
B.50+50(1+m)2万元;
C.50+50(1+2m)万元
D.50+50(1+m)+50(1+m)2万元
反馈练习巩固新知
2.某村家用电脑总量,2020年
比2018年增长69%,若设平均每年
的增长率为x,依题意得方程:___________;
3.西瓜经营户以2元/千克的价格购进一批小型西瓜,
以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元
课堂小结布置作业
小结:
利用方程解决实际问题的关键和步骤:
关键:寻找等量关系
步骤:
一是整体地、系统地审清问题;
二是把握问题中的“相等关系”;
三是正确求解方程并检验解的合理性。
课堂小结布置作业
作业:
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如图对话中收费标准.某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少员工去天水湾风景区旅游?
如果人数超过25人,每增加1人,人均旅游费用降低20元,但人均旅游费用不得低于700元.
如果人数不超过25人,人均旅游费用为1000元.
2.6 应用一元二次方程
第1课时 几何动点问题与图形面积
创设情境 温故探新
复习
导入
还记得本章开始时梯子下滑的问题吗?
①在这个问题中,梯子顶端下滑1米时,梯子底端滑动的距离大于1米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?呢?
②如果梯子长度是13米,梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
合作交流探究新知
如图:某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头。小岛F位于BC中点。一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰。
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
合作交流探究新知
(1)要求DE的长,需要如何设未知数?
(2)怎样建立含DE未知数的等量关系?从已知条件中能找到吗?
(3)利用勾股定理建立等量关系,如何构造直角三角形?
(4)选定Rt△DEF后,三条边长都是已知的吗?DE,DF,EF分别是多少?
合作交流探究新知
速度等量:V军舰=2×V补给船
时间等量:t军舰=t补给船
三边数量关系:EF2+FD2=DE2
例1:
范例研讨运用新知
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A 、C同时出发,点P以3 cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动。问几秒后,点P和点Q的距离是10 cm?
A
B
C
D
P
Q
E
范例研讨运用新知
解:设t秒后,点P和点Q的距离是10 cm,则AP=3t,CQ=2t
过点P作PE⊥CD于E
所以四边形APDE是矩形,所以AD=PE=6cm
EQ=16-2t-3t=16-5t
在直角三角形PQE中,PQ2=PE2+EQ2
100=62+(16-5t)2
解这个方程,得,
答:秒或秒后,点P和点Q的距离是10 cm
反馈练习巩固新知
1. 一架长为10米的梯子斜靠在墙
上,梯子的顶端距地面的垂直距
离为6米,如果梯子的顶端沿墙
壁下滑1米,那么梯子的底端向后滑动的距( )
A 等于1米 B 大于1米 C 小于1米 D 不能确定
2.某生活小区准备在每幢楼房之间,开辟面积为200平方米的一块长方形绿地,并且长比宽多10米,则绿地的长为_____米,宽为_______米;
反馈练习巩固新知
3.下图是中北居民小区某一休闲场所
的平面示意图.图中阴影部分是草
坪和健身器材安装区,空白部分是用做散步的道路.东西方向的一条主干道较宽,
其余道路的宽度相等,主干道的
宽度是其余道路的宽度的2倍.
这块休闲场所南北长18m,东西宽
16m.已知这休闲场地中草坪和健
身器材安装区的面积为168m2,
请问主干道的宽度为多少米?
北
西
东
课堂小结布置作业
小结:
列方程解应用题的一般步骤:
(1)审题.了解问题的实际意义,分清已知条件和未知量之间的关系.
(2)设未知数.一般情况下求什么设什么为未知数.
(3)列方程.根据量与量之间的关系,找出相等关系,列出方程.
(4)解方程.灵活运用一元二次方程的四种解法.
(5)验根.检验一元二次方程的根是否满足题意.
(6)答.作答.
课堂小结布置作业
作业:
如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动。能使△PBQ的面积为15cm2 的是多少秒?
B
A
C
P
Q
2.6 应用一元二次方程
第2课时 利润与变化率
创设情境 温故探新
复习
导入
请同学们回忆并回答与利润相关的知识
利润率=________
利润=_____-进价
售价=标价×折扣
9折要乘以90%或0.9或 ,
那么x折呢?
合作交流探究新知
例2:
新华商场销售某种冰箱,每台进货价为
2500元。市场调研表明:当销售价为2900元时,
平均每天能售出8台;而当销售价每降低50元时,
平均每天就能多售出4台。商场要想使这种冰箱
的销售利润平均每天达到5000元,每台冰箱的
降价应为多少元?
合作交流探究新知
(1)要求每台冰箱的定价应为多少元,
需要如何设未知数?
(2)降价后每台冰箱的利润是多少?
(3)降价后卖出冰箱的台数?
本题的主要等量关系:
每台冰箱的销售利润×平均每天的销售台数=5000
范例研讨运用新知
将进货单价为40元的商品按50元售出时,就能卖出500个.已知这种商品每个涨价1元,其销售量就减少10个,问为了赚得8000元的利润,售价应定为多少?这时应进货多少个?
范例研讨运用新知
解:设商品的单价是(50+x)元,则每个商品的利润是[(50+x)-40]元,销售量是(500-10x)个.
[(50+x)-40](500-10x)=8000
x2-40x+300=0
x1=10,x2=30
故商品的的单价可定为50+10=60元或50+30=80元.
当单价为60元时,其进货量只能是500-10×10=400个;
当单价为80元时,其进货量只能是500-10×30=200个.
答:为了赚得8000元的利润,售价应定为60元,这时应进货多400个或定为80元,这时应进货200个.
反馈练习巩固新知
1.裕丰商店一月份的利润为50万元,二、三月份的利润平均增长率为m,下列各式中,正确表示这个商店第一季度的总利润的是( )
A.50[m2+3m+3] 万元
B.50+50(1+m)2万元;
C.50+50(1+2m)万元
D.50+50(1+m)+50(1+m)2万元
反馈练习巩固新知
2.某村家用电脑总量,2020年
比2018年增长69%,若设平均每年
的增长率为x,依题意得方程:___________;
3.西瓜经营户以2元/千克的价格购进一批小型西瓜,
以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元
课堂小结布置作业
小结:
利用方程解决实际问题的关键和步骤:
关键:寻找等量关系
步骤:
一是整体地、系统地审清问题;
二是把握问题中的“相等关系”;
三是正确求解方程并检验解的合理性。
课堂小结布置作业
作业:
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如图对话中收费标准.某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少员工去天水湾风景区旅游?
如果人数超过25人,每增加1人,人均旅游费用降低20元,但人均旅游费用不得低于700元.
如果人数不超过25人,人均旅游费用为1000元.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
