2021—2022学年华东师大版数学八年级上册13.2.5边边边 课件(17张)
文档属性
| 名称 | 2021—2022学年华东师大版数学八年级上册13.2.5边边边 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
华东师大版八年级上
13.2.5 边边边 课件
1、图形变换(翻折、平移、旋转)
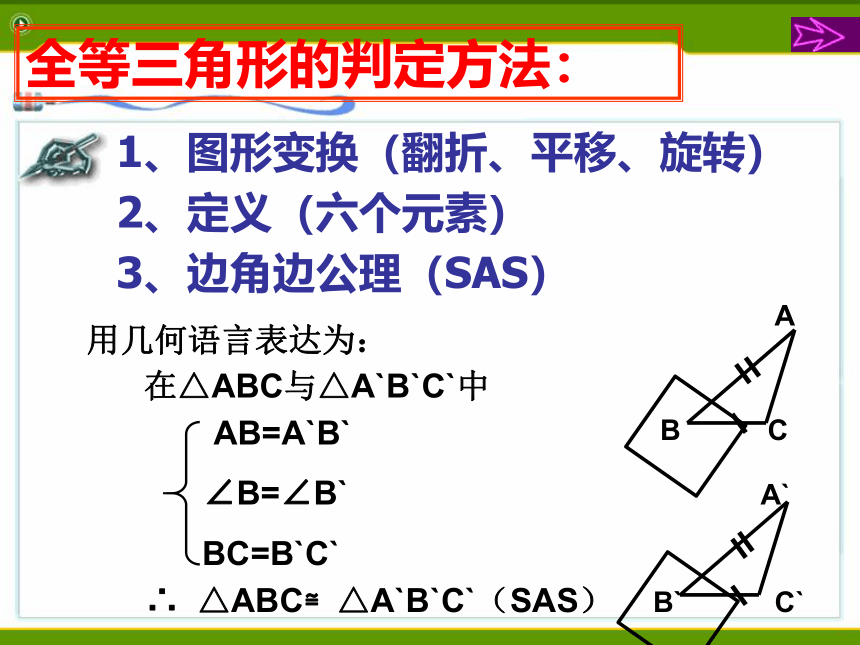
全等三角形的判定方法:
3、边角边公理(SAS)
2、定义(六个元素)
用几何语言表达为:
在△ABC与△A`B`C`中
∴ △ABC≌△A`B`C`(SAS)
AB=A`B`
∠B=∠B`
BC=B`C`
A
B
C
A`
B`
C`
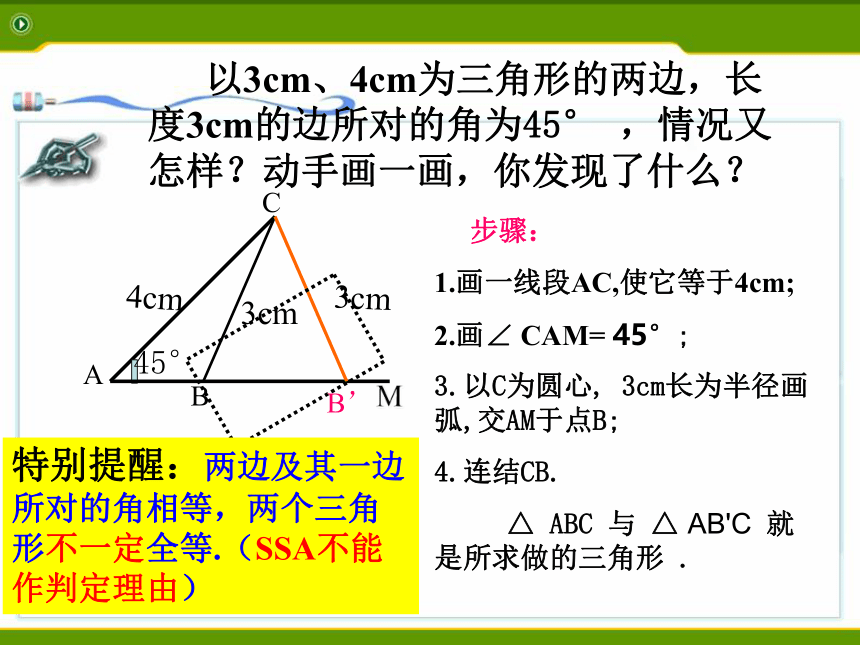
以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?
4cm
3cm
45°
A
3cm
步骤:
1.画一线段AC,使它等于4cm;
2.画∠ CAM= 45°;
3.以C为圆心, 3cm长为半径画弧,交AM于点B;
4.连结CB.
△ ABC 与 △ AB'C 就是所求做的三角形 .
显然: △ ABC与△ AB'C不全等
B
B’
M
C
特别提醒:两边及其一边所对的角相等,两个三角形不一定全等.(SSA不能作判定理由)
1、图形变换(翻折、平移、旋转)
全等三角形的判定方法:
3、边角边公理(SAS)
2、定义(六个元素)
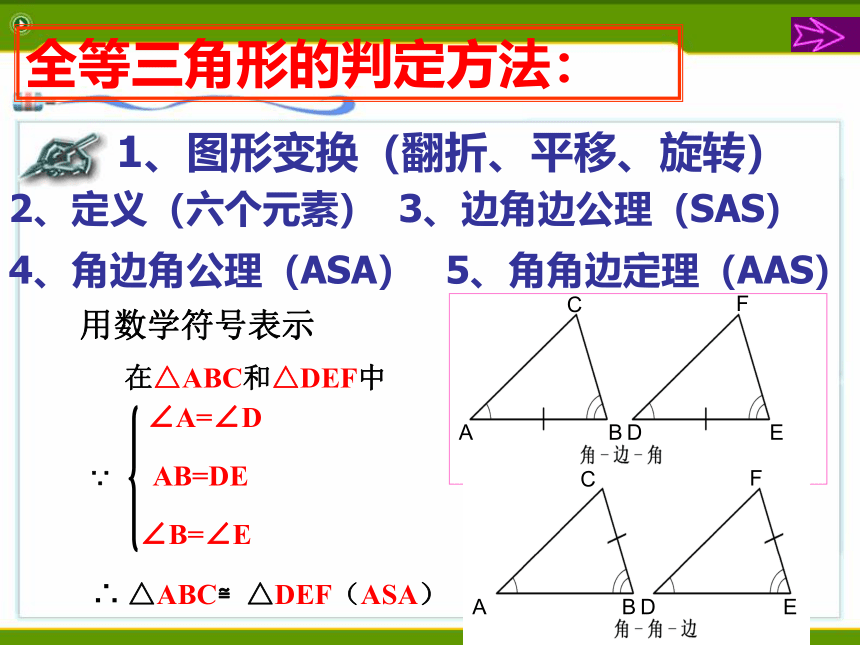
4、角边角公理(ASA)
5、角角边定理(AAS)
用数学符号表示
∠A=∠D
∵ AB=DE
∠B=∠E
在△ABC和△DEF中
∴ △ABC≌△DEF(ASA)
A
B
C
D
E
F
A
B
C
D
E
F
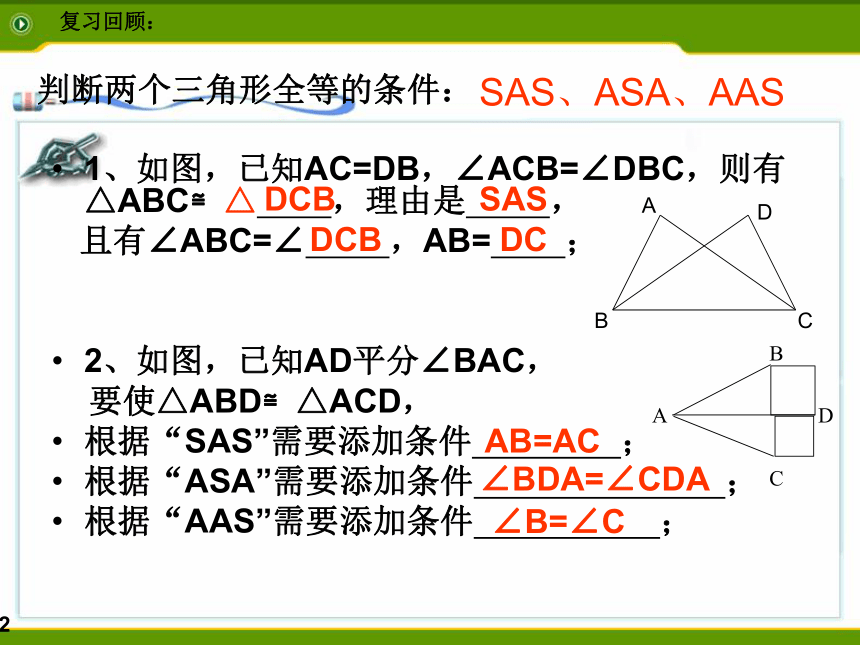
1、如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC=∠ ,AB= ;
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
A
B
C
D
A
B
C
D
DCB
判断两个三角形全等的条件:
SAS
DCB
DC
AB=AC
∠BDA=∠CDA
∠B=∠C
SAS、ASA、AAS
2
复习回顾:
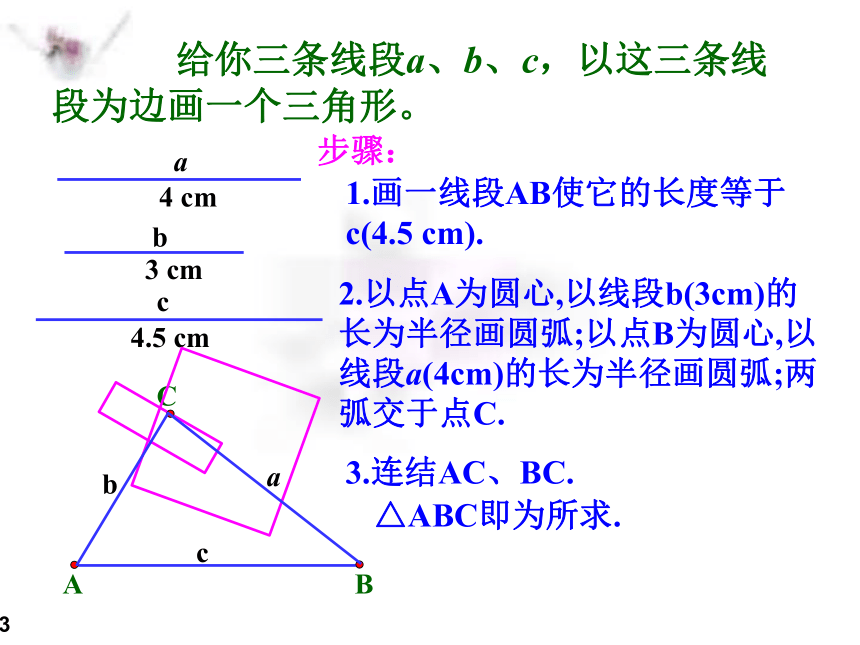
给你三条线段a、b、c,以这三条线段为边画一个三角形。
4 cm
a
3 cm
b
4.5 cm
c
步骤:
1.画一线段AB使它的长度等于 c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
3.连结AC、BC.
a
b
c
A
B
C
△ABC即为所求.
3
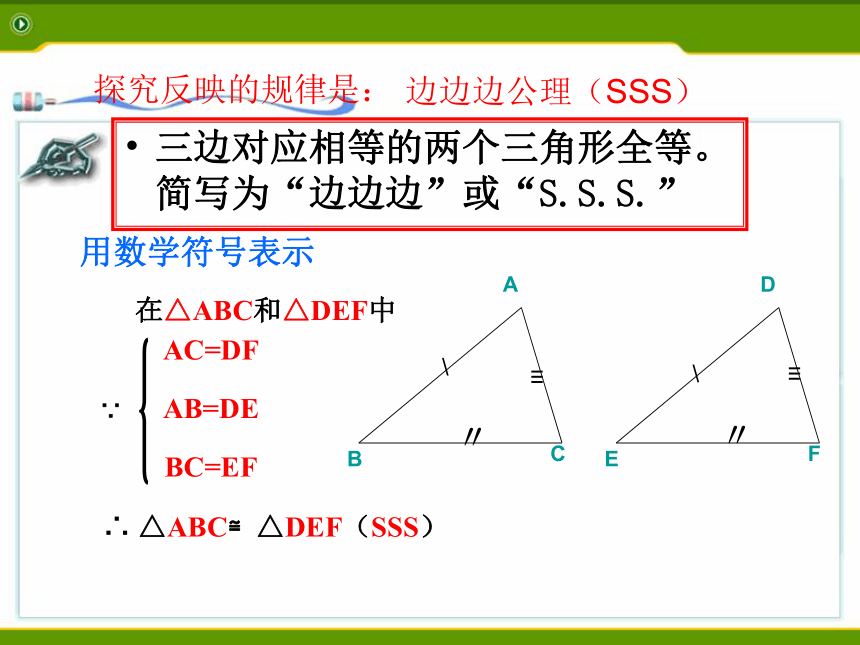
探究反映的规律是:
用数学符号表示
AC=DF
∵ AB=DE
BC=EF
在△ABC和△DEF中
∴ △ABC≌△DEF(SSS)
边边边公理(SSS)
三边对应相等的两个三角形全等。简写为“边边边”或“S.S.S.”
A
B
C
D
E
F
〃
〃
\
\
≡
≡
例1:
已知如图, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
解: 在△ABC 和△CDA中,
AD=BC(已知),
∵ AB=CD(已知),
AC=CA(公共边),
△ABC ≌△CDA(S.S.S.)
∴
A
B
C
D
7
已知如图,在四边形ABCD中,AD=BC,
AB=CD,求证:
D
D
A
B
C
(1) ∠B=∠D ;
你还能得到什么结论?
(2) AB∥CD ;
(3) AD∥BC
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S.)
不一定
一定
(A.S.A.)
一定
(A.A.S.)
一定
(S.S.S.)
不一定
归纳
特别关注边角的位置哦
判定三角形全等至少要有一组边!
10
已知如图,AB=DC,AC=DB,△ABC与△DCB全等吗?为什么?
A
B
C
D
O
△ABO与△DCO全等吗?
11
2. 如图,AC、BD相交于点O,且 AB=DC,AC=BD,求证:(1)∠A=∠D
(2)OB=OC
A
B
C
D
O
提示:做辅助线
12
B
A
E
D
C
已知:如图,AB=AC,AD=AE,BD=CE,则图中有_____对三角形全等?
如图,在△ABC中,AB=AC,E、F分别为AB、AC上的点,且AE=AF,BF与CE相交于点O。
A
O
F
E
B
C
1、图中有哪些全等的三角形?
△ABF≌△ACE(SAS)
△EBC≌△FCB(SSS)
△EBO≌△FCO(AAS)
2、图中有哪些相等的线段?
3、图中有哪些相等的角?
一、填空题:
1.如图,已知AB=CE,AD=BC,则图中共有全等三角形的对数是 。
2.如图,AD平分∠ BAC,AB=AC,连结BD,CD,并延长交AC,AB于点F、E,则此图形中有 对全等三角形。
A
B
C
D
A
B
C
D
E
F
二、填空题:
3、已知如图, ∠ACB= ∠DBC,如果要使△ ABC ≌△ DCB,只需增加一个条件是_____________
A
B
C
D
O
4、已知如图,AB=AD,CB=CD,E是AC上一点,求证:BE=DE
A
B
C
D
E
三、证明题:
华东师大版八年级上
13.2.5 边边边 课件
1、图形变换(翻折、平移、旋转)
全等三角形的判定方法:
3、边角边公理(SAS)
2、定义(六个元素)
用几何语言表达为:
在△ABC与△A`B`C`中
∴ △ABC≌△A`B`C`(SAS)
AB=A`B`
∠B=∠B`
BC=B`C`
A
B
C
A`
B`
C`
以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?
4cm
3cm
45°
A
3cm
步骤:
1.画一线段AC,使它等于4cm;
2.画∠ CAM= 45°;
3.以C为圆心, 3cm长为半径画弧,交AM于点B;
4.连结CB.
△ ABC 与 △ AB'C 就是所求做的三角形 .
显然: △ ABC与△ AB'C不全等
B
B’
M
C
特别提醒:两边及其一边所对的角相等,两个三角形不一定全等.(SSA不能作判定理由)
1、图形变换(翻折、平移、旋转)
全等三角形的判定方法:
3、边角边公理(SAS)
2、定义(六个元素)
4、角边角公理(ASA)
5、角角边定理(AAS)
用数学符号表示
∠A=∠D
∵ AB=DE
∠B=∠E
在△ABC和△DEF中
∴ △ABC≌△DEF(ASA)
A
B
C
D
E
F
A
B
C
D
E
F
1、如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC=∠ ,AB= ;
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
A
B
C
D
A
B
C
D
DCB
判断两个三角形全等的条件:
SAS
DCB
DC
AB=AC
∠BDA=∠CDA
∠B=∠C
SAS、ASA、AAS
2
复习回顾:
给你三条线段a、b、c,以这三条线段为边画一个三角形。
4 cm
a
3 cm
b
4.5 cm
c
步骤:
1.画一线段AB使它的长度等于 c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
3.连结AC、BC.
a
b
c
A
B
C
△ABC即为所求.
3
探究反映的规律是:
用数学符号表示
AC=DF
∵ AB=DE
BC=EF
在△ABC和△DEF中
∴ △ABC≌△DEF(SSS)
边边边公理(SSS)
三边对应相等的两个三角形全等。简写为“边边边”或“S.S.S.”
A
B
C
D
E
F
〃
〃
\
\
≡
≡
例1:
已知如图, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
解: 在△ABC 和△CDA中,
AD=BC(已知),
∵ AB=CD(已知),
AC=CA(公共边),
△ABC ≌△CDA(S.S.S.)
∴
A
B
C
D
7
已知如图,在四边形ABCD中,AD=BC,
AB=CD,求证:
D
D
A
B
C
(1) ∠B=∠D ;
你还能得到什么结论?
(2) AB∥CD ;
(3) AD∥BC
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S.)
不一定
一定
(A.S.A.)
一定
(A.A.S.)
一定
(S.S.S.)
不一定
归纳
特别关注边角的位置哦
判定三角形全等至少要有一组边!
10
已知如图,AB=DC,AC=DB,△ABC与△DCB全等吗?为什么?
A
B
C
D
O
△ABO与△DCO全等吗?
11
2. 如图,AC、BD相交于点O,且 AB=DC,AC=BD,求证:(1)∠A=∠D
(2)OB=OC
A
B
C
D
O
提示:做辅助线
12
B
A
E
D
C
已知:如图,AB=AC,AD=AE,BD=CE,则图中有_____对三角形全等?
如图,在△ABC中,AB=AC,E、F分别为AB、AC上的点,且AE=AF,BF与CE相交于点O。
A
O
F
E
B
C
1、图中有哪些全等的三角形?
△ABF≌△ACE(SAS)
△EBC≌△FCB(SSS)
△EBO≌△FCO(AAS)
2、图中有哪些相等的线段?
3、图中有哪些相等的角?
一、填空题:
1.如图,已知AB=CE,AD=BC,则图中共有全等三角形的对数是 。
2.如图,AD平分∠ BAC,AB=AC,连结BD,CD,并延长交AC,AB于点F、E,则此图形中有 对全等三角形。
A
B
C
D
A
B
C
D
E
F
二、填空题:
3、已知如图, ∠ACB= ∠DBC,如果要使△ ABC ≌△ DCB,只需增加一个条件是_____________
A
B
C
D
O
4、已知如图,AB=AD,CB=CD,E是AC上一点,求证:BE=DE
A
B
C
D
E
三、证明题:
