2021—2022学年华东师大版数学九年级上册23.3.2相似三角形的判定(三)课件(16张)
文档属性
| 名称 | 2021—2022学年华东师大版数学九年级上册23.3.2相似三角形的判定(三)课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 836.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 10:57:56 | ||
图片预览




文档简介
(共16张PPT)
23.3相似三角形
23.3.2相似三角形的判定(三)
试一试
下面两个三角形中, ,求证△ABC∽△A′B′C′.
A
B
C
C′
B′
A′
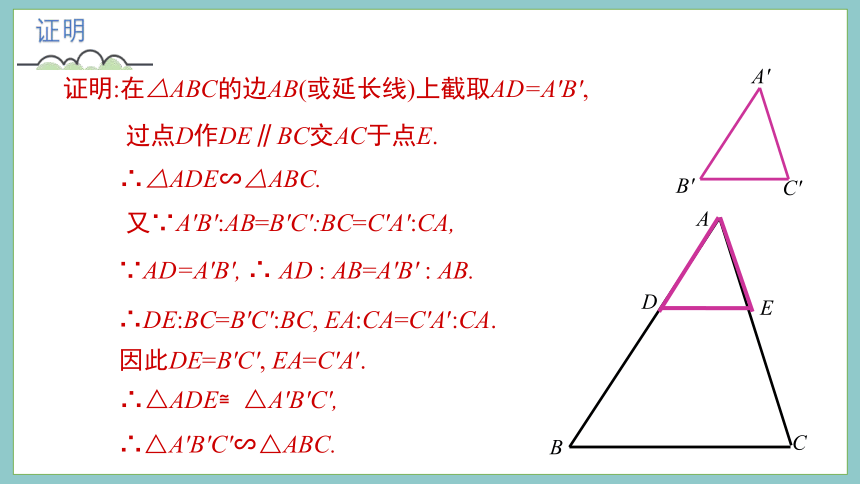
证明
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A′
B′
C′
A
C
D
E
过点D作DE∥BC交AC于点E.
又∵A′B′:AB=B′C′:BC=C′A′:CA,
∴△ADE∽△ABC.
∵AD=A′B′, ∴ AD : AB=A′B′ : AB.
∴DE:BC=B′C′:BC, EA:CA=C′A′:CA.
因此DE=B′C′, EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′,
B
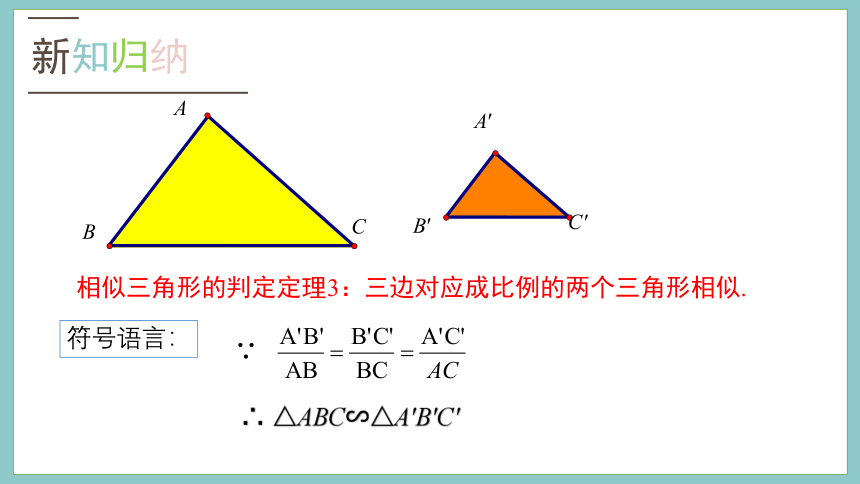
新知归纳
∴ △ABC∽△A′B′C′
相似三角形的判定定理3:三边对应成比例的两个三角形相似.
A
B
C
C′
B′
A′
符号语言:
1.已知AB=10,BC=8 ,AC=16,A′B′=16,B′C′=12.8, C′A′=25.6,试说明△ABC∽△A′B′C′.
∴△ABC∽△A′B′C′.
练习
判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最长边与最长边对应,最短边与最短边对应.
方法归纳
练习
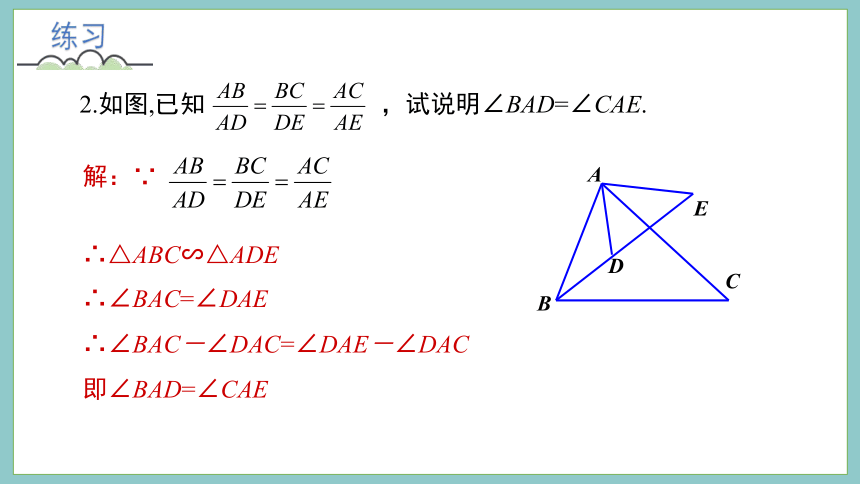
2.如图,已知 ,试说明∠BAD=∠CAE.
A
D
C
E
B
解:∵
∴△ABC∽△ADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
练习
4. 如图,在Rt△AOD中,∠AOD=90°,点B,C在OD上,且OA=OB=BC=CD,求证:△ABC ∽△DBA.
练习
当堂练习
2.若△ABC各边分别为AB=10 cm,BC=8 cm,AC=6 cm,△DEF的两边为DE=5 cm,EF=4 cm,则当DF=________cm时,△ABC∽△DEF.
3
A
当堂练习
3.下列说法:①所有等腰三角形都相似:②有一个底角相等的两个等腰三角形相似:③有一个角相等的两个等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法有__________
② ④
实践与探究丛书50页,变式1
实践与探究丛书50页,例3
实践与探究丛书50页,变式4
三边成比例的两个三角形相似
利用三边判定两个三角形相似
课堂小结
相似三角形的判定定理的运用
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
23.3相似三角形
23.3.2相似三角形的判定(三)
试一试
下面两个三角形中, ,求证△ABC∽△A′B′C′.
A
B
C
C′
B′
A′
证明
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A′
B′
C′
A
C
D
E
过点D作DE∥BC交AC于点E.
又∵A′B′:AB=B′C′:BC=C′A′:CA,
∴△ADE∽△ABC.
∵AD=A′B′, ∴ AD : AB=A′B′ : AB.
∴DE:BC=B′C′:BC, EA:CA=C′A′:CA.
因此DE=B′C′, EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′,
B
新知归纳
∴ △ABC∽△A′B′C′
相似三角形的判定定理3:三边对应成比例的两个三角形相似.
A
B
C
C′
B′
A′
符号语言:
1.已知AB=10,BC=8 ,AC=16,A′B′=16,B′C′=12.8, C′A′=25.6,试说明△ABC∽△A′B′C′.
∴△ABC∽△A′B′C′.
练习
判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最长边与最长边对应,最短边与最短边对应.
方法归纳
练习
2.如图,已知 ,试说明∠BAD=∠CAE.
A
D
C
E
B
解:∵
∴△ABC∽△ADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
练习
4. 如图,在Rt△AOD中,∠AOD=90°,点B,C在OD上,且OA=OB=BC=CD,求证:△ABC ∽△DBA.
练习
当堂练习
2.若△ABC各边分别为AB=10 cm,BC=8 cm,AC=6 cm,△DEF的两边为DE=5 cm,EF=4 cm,则当DF=________cm时,△ABC∽△DEF.
3
A
当堂练习
3.下列说法:①所有等腰三角形都相似:②有一个底角相等的两个等腰三角形相似:③有一个角相等的两个等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法有__________
② ④
实践与探究丛书50页,变式1
实践与探究丛书50页,例3
实践与探究丛书50页,变式4
三边成比例的两个三角形相似
利用三边判定两个三角形相似
课堂小结
相似三角形的判定定理的运用
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
