2021-2022学年人教版七年级上册3.2 移项 课件(32张)
文档属性
| 名称 | 2021-2022学年人教版七年级上册3.2 移项 课件(32张) |  | |
| 格式 | zip | ||
| 文件大小 | 705.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 10:59:08 | ||
图片预览









文档简介
(共32张PPT)
解一元一次方程
——移项
运用等式的性质解下列方程
复习回顾
1
(1) x + 2 = 1
x + 2 -2 = 1-2.
x =-1.
解:两边都减去2,得
等式的性质1
合并同类项,得
即:等式两边都加上或减去同一个数或同一个整式,所得结果仍是等式.
(2) 3x = -6
即:x =-2.
解:两边都除以3,得
等式的性质2
即:等式两边都乘或除以同一个不等于0的数,所得结果仍是等式.
一般地,把方程中的项改变符号后,从方程
的一边移到另一边,这种变形叫做移项
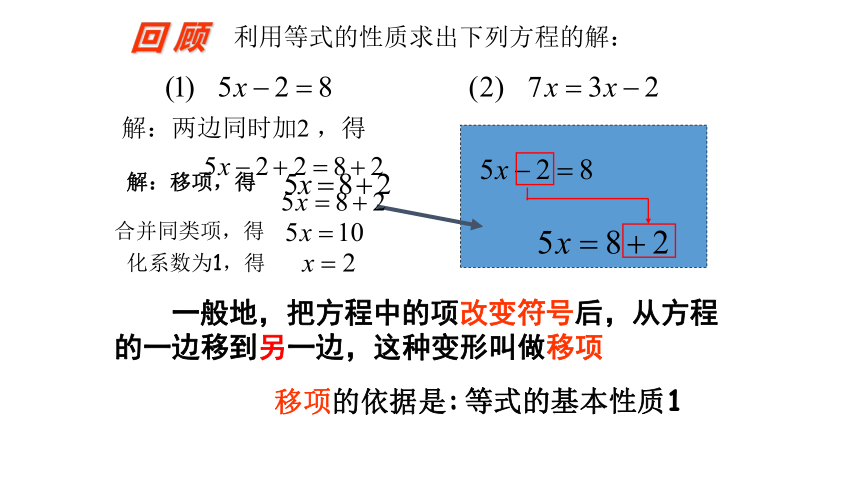
利用等式的性质求出下列方程的解:
回 顾
解:两边同时加2 ,得
合并同类项,得
化系数为1,得
解:移项,得
移项的依据是:
等式的基本性质1
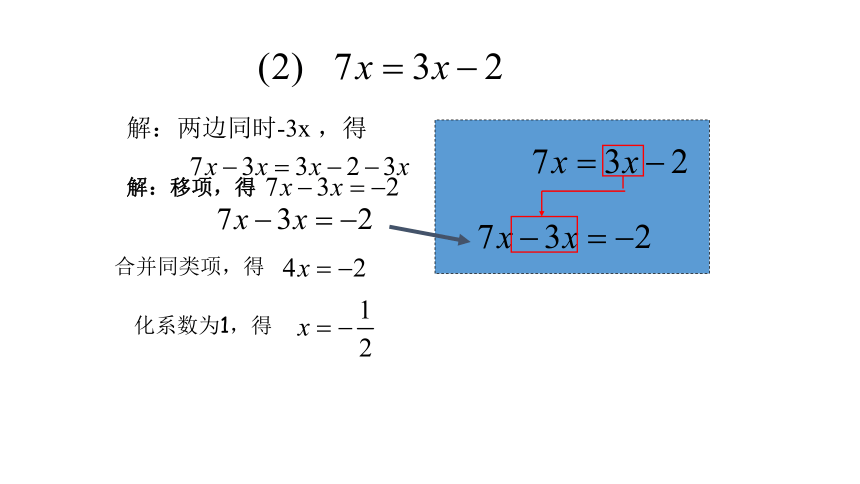
解:两边同时-3x ,得
合并同类项,得
化系数为1,得
解:移项,得
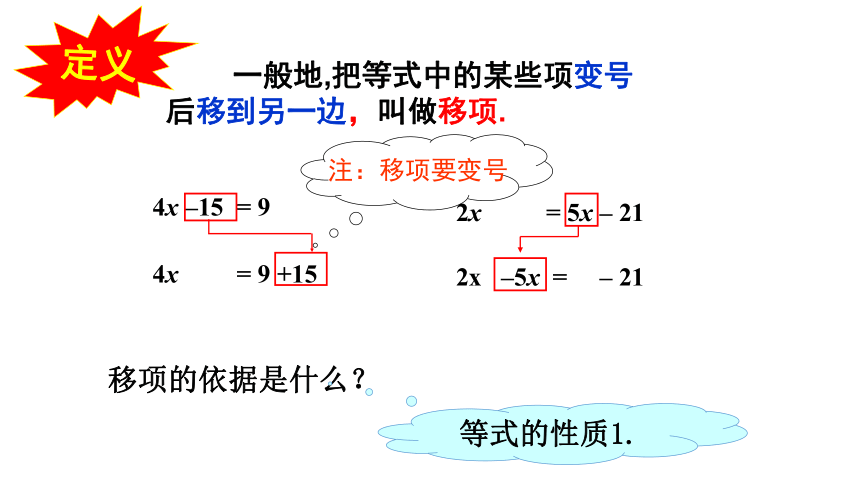
一般地,把等式中的某些项变号
后移到另一边,叫做移项.
定义
2x = 5x – 21
2x –5x = – 21
4x –15 = 9
4x = 9 +15
注:移项要变号
移项的依据是什么?
等式的性质1.
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
以上解方程中“移项”起了什么作用?
请你判断
下列方程变形是否正确?
(1) 6+x=8,移项得x=8+6
(2) 3x=8-2x,移项得3x+2x=-8
(3) 5x-2=3x+7,移项得5x+3x=7+2
(4) -x+3x=8,移项得3x+x=8
错
3x-x=8
错
x=8-6
错
3x+2x=8
错
5x-3x=7+2
下面的移项对不对?如果不对,请改正?
(1)从5+2x=10,得2x=10+5
(2)从3x=2x-5,得3x+2x=5
(3) 从-2x+5=1-3x,得-2x+3x=1+5
2x=10-5
3x-2x=-5
-2x+3x=1-5
练一练
下列移项正确的是( )
A.由2+x=8,得到x=8+2
B.由5x=-8+x,得到5x+x= -8
C.由4x=2x+1,得到4x-2x=1
D.由5x-3=0,得到5x=-3
C
练一练
下面方程的解法对吗?如果不对,应怎样改正?
解:移项,得
合并同类项,得
系数化为1,得
A、将方程3X- 3 =0移项得3X =3
B、将方程4y -1 =5y+3移项得4y – 5y=3+1
C、将方程-3X=12两边同时除以-3得x= - 4
D、将方程6x=5x两边同时除以x得6=5
D
A、由5+3x -2y,得3x -2y+5
B、由-10x-5=-2x,得10x-2x=5
C、由5x=10,得x=2
D、由7x+9=4x-1得7x-4x=-1-9
目标检测
1、下列方程变形中,错误的是( )
2、下列计算,其中属于移项变形的是( )
D
3、对于方程7x-1=5+4x,
移项,得 ,
合并同类项,得 ,
系数化为1,得 。
例1:解下列方程
(2)
(1)
移项时应注意改变项的符号
运用新知
“移项”应注意什么?
x = -2
解:移项,得
合并同类项,得
系数化为1,得
解:移项,得
合并同类项,得
系数化为1,得
例2:解下列方程.
解:移项,得
6x-3x=8+7
合并同类项,得
3x=15.
系数化为1,得
x=5.
6x-7=3x+8
6x-3x=8+7
移项时应注意改变项的符号
解:移项,得
合并同类项,得
系数化成1,得
例3:解下列方程
解:移项,得
(1)3x +7 = 32 - 2x
移项时应注意改变项的符号
运用新知
“移项”应注意什么?
3x + 2x = 32 - 7
5x = 25
x = 5
合并同类项,得
系数化为1,得
解:移项,得
合并同类项,得
系数化为1,得
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
思考:
(1)你认为题中涉及到哪些数量关系和相等关系?
(2)你认为引进什么样的未知数,根据这样的相等
关系列出方程?
(一)创设情境,列出方程
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出 本,加上剩余
的20本,这批书共 本.
每人分4本,需要 本,减去缺少
的25本,这批书共 本.
分析
设这个班有x名学生.
这批书的总数有几种
表示法?
它们之间有什么关系?
表示这批书的总数的两个代数式相等.
(一)创设情境,列出方程
3x +20 = 4x -25
3x-4x=-25 -20
-x=-45
X=45
合并同类项,得
例3 某制药厂制造一批药品,如用旧工艺,则废水排量要比
环保限制的最大量还多200 t ;如用新工艺,则废水排量比环
保限制的最大量少100 t .新、旧工艺的废水排量之比为
2:5,两种工艺的废水排量各是多少
系数化为1,得
解:设新、旧工艺的废水排量分别是 2x t 和 5x t
5x -200 = 2x +100
x =100
答:新旧工艺的废水派量分别是 200 t 和500 t
由题意得 环保限制的最大量是
5x - 2x = 100 +200
移项,得
3x =300
2x =200
5x =500
所以有
1. :一般地,把等式中的某些项、变号后移到另一边,叫做移项。
3.移项要改变符号.
2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
移项
1.简单方程解法步骤
移项;
合并同类项;
系数化为1.
课堂小结
2.用一元一次方程分析并解决实际问题的基本过程:
实际问题
数学问题
(一元一次方程)
实际问题
的答案
数学问题的解
(x=a)
检验
列方程
解方程
1、已知2x+1与-12x+5的值是相反数,求x的值.
拓展思维
2、已知:y1 = 2x+1, y2 = 3 -x.当x取何值时, y1 = y2 ?
补充练习:
天平的左边放2枚硬币和13克砝码,右边放6枚硬币和5克砝码,此时天平恰好平衡.每枚硬币的质量是多少克?
解:设每枚硬币的质量是 克.
解得
答:每枚硬币的质量是2克.
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法一:设这个班共有同学x人.则
得出 x=36
答:这个班共有36人.
综合应用
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法二:设船有x条.则
6(x+1)=9(x-1)
得出 x=5
6× (5+1)=36(人)
答:这个班共有36人.
练一练:解下列一元一次方程:
(1)8人分别乘两辆小汽车赶往火车站,其中一辆小汽车在距离火车站15千米的地方出了故障,此时离火车停止检票时间还有42分,这时唯一可以利用的交通工具只有一辆小汽车,连司机在内限乘5人,这辆小汽车的平均速度为60千米/时,这8人能赶上火车吗?(设走行速度为5千米/时).
练一练
第一种情况:
小汽车分二批送这8人,若第二批人在原地不动,那么小汽车来回要走15×3=45千米,所需
时间为 =45分>42分,因此,单靠汽车来回接送无法使8人都赶上火车.
第二种情况:
若在汽车送第一批人的同时,其他人先步行,可以节省时间,汽车送完第一批人后,用了x
解:此题可分类讨论:
小时与第二批人相遇,再用x小时送到火车站,则列方程得,
解得:
所用时间为: 时,
因为40.4<42,因此,这时8人能赶上火车.
解一元一次方程
——移项
运用等式的性质解下列方程
复习回顾
1
(1) x + 2 = 1
x + 2 -2 = 1-2.
x =-1.
解:两边都减去2,得
等式的性质1
合并同类项,得
即:等式两边都加上或减去同一个数或同一个整式,所得结果仍是等式.
(2) 3x = -6
即:x =-2.
解:两边都除以3,得
等式的性质2
即:等式两边都乘或除以同一个不等于0的数,所得结果仍是等式.
一般地,把方程中的项改变符号后,从方程
的一边移到另一边,这种变形叫做移项
利用等式的性质求出下列方程的解:
回 顾
解:两边同时加2 ,得
合并同类项,得
化系数为1,得
解:移项,得
移项的依据是:
等式的基本性质1
解:两边同时-3x ,得
合并同类项,得
化系数为1,得
解:移项,得
一般地,把等式中的某些项变号
后移到另一边,叫做移项.
定义
2x = 5x – 21
2x –5x = – 21
4x –15 = 9
4x = 9 +15
注:移项要变号
移项的依据是什么?
等式的性质1.
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
以上解方程中“移项”起了什么作用?
请你判断
下列方程变形是否正确?
(1) 6+x=8,移项得x=8+6
(2) 3x=8-2x,移项得3x+2x=-8
(3) 5x-2=3x+7,移项得5x+3x=7+2
(4) -x+3x=8,移项得3x+x=8
错
3x-x=8
错
x=8-6
错
3x+2x=8
错
5x-3x=7+2
下面的移项对不对?如果不对,请改正?
(1)从5+2x=10,得2x=10+5
(2)从3x=2x-5,得3x+2x=5
(3) 从-2x+5=1-3x,得-2x+3x=1+5
2x=10-5
3x-2x=-5
-2x+3x=1-5
练一练
下列移项正确的是( )
A.由2+x=8,得到x=8+2
B.由5x=-8+x,得到5x+x= -8
C.由4x=2x+1,得到4x-2x=1
D.由5x-3=0,得到5x=-3
C
练一练
下面方程的解法对吗?如果不对,应怎样改正?
解:移项,得
合并同类项,得
系数化为1,得
A、将方程3X- 3 =0移项得3X =3
B、将方程4y -1 =5y+3移项得4y – 5y=3+1
C、将方程-3X=12两边同时除以-3得x= - 4
D、将方程6x=5x两边同时除以x得6=5
D
A、由5+3x -2y,得3x -2y+5
B、由-10x-5=-2x,得10x-2x=5
C、由5x=10,得x=2
D、由7x+9=4x-1得7x-4x=-1-9
目标检测
1、下列方程变形中,错误的是( )
2、下列计算,其中属于移项变形的是( )
D
3、对于方程7x-1=5+4x,
移项,得 ,
合并同类项,得 ,
系数化为1,得 。
例1:解下列方程
(2)
(1)
移项时应注意改变项的符号
运用新知
“移项”应注意什么?
x = -2
解:移项,得
合并同类项,得
系数化为1,得
解:移项,得
合并同类项,得
系数化为1,得
例2:解下列方程.
解:移项,得
6x-3x=8+7
合并同类项,得
3x=15.
系数化为1,得
x=5.
6x-7=3x+8
6x-3x=8+7
移项时应注意改变项的符号
解:移项,得
合并同类项,得
系数化成1,得
例3:解下列方程
解:移项,得
(1)3x +7 = 32 - 2x
移项时应注意改变项的符号
运用新知
“移项”应注意什么?
3x + 2x = 32 - 7
5x = 25
x = 5
合并同类项,得
系数化为1,得
解:移项,得
合并同类项,得
系数化为1,得
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
思考:
(1)你认为题中涉及到哪些数量关系和相等关系?
(2)你认为引进什么样的未知数,根据这样的相等
关系列出方程?
(一)创设情境,列出方程
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出 本,加上剩余
的20本,这批书共 本.
每人分4本,需要 本,减去缺少
的25本,这批书共 本.
分析
设这个班有x名学生.
这批书的总数有几种
表示法?
它们之间有什么关系?
表示这批书的总数的两个代数式相等.
(一)创设情境,列出方程
3x +20 = 4x -25
3x-4x=-25 -20
-x=-45
X=45
合并同类项,得
例3 某制药厂制造一批药品,如用旧工艺,则废水排量要比
环保限制的最大量还多200 t ;如用新工艺,则废水排量比环
保限制的最大量少100 t .新、旧工艺的废水排量之比为
2:5,两种工艺的废水排量各是多少
系数化为1,得
解:设新、旧工艺的废水排量分别是 2x t 和 5x t
5x -200 = 2x +100
x =100
答:新旧工艺的废水派量分别是 200 t 和500 t
由题意得 环保限制的最大量是
5x - 2x = 100 +200
移项,得
3x =300
2x =200
5x =500
所以有
1. :一般地,把等式中的某些项、变号后移到另一边,叫做移项。
3.移项要改变符号.
2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
移项
1.简单方程解法步骤
移项;
合并同类项;
系数化为1.
课堂小结
2.用一元一次方程分析并解决实际问题的基本过程:
实际问题
数学问题
(一元一次方程)
实际问题
的答案
数学问题的解
(x=a)
检验
列方程
解方程
1、已知2x+1与-12x+5的值是相反数,求x的值.
拓展思维
2、已知:y1 = 2x+1, y2 = 3 -x.当x取何值时, y1 = y2 ?
补充练习:
天平的左边放2枚硬币和13克砝码,右边放6枚硬币和5克砝码,此时天平恰好平衡.每枚硬币的质量是多少克?
解:设每枚硬币的质量是 克.
解得
答:每枚硬币的质量是2克.
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法一:设这个班共有同学x人.则
得出 x=36
答:这个班共有36人.
综合应用
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法二:设船有x条.则
6(x+1)=9(x-1)
得出 x=5
6× (5+1)=36(人)
答:这个班共有36人.
练一练:解下列一元一次方程:
(1)8人分别乘两辆小汽车赶往火车站,其中一辆小汽车在距离火车站15千米的地方出了故障,此时离火车停止检票时间还有42分,这时唯一可以利用的交通工具只有一辆小汽车,连司机在内限乘5人,这辆小汽车的平均速度为60千米/时,这8人能赶上火车吗?(设走行速度为5千米/时).
练一练
第一种情况:
小汽车分二批送这8人,若第二批人在原地不动,那么小汽车来回要走15×3=45千米,所需
时间为 =45分>42分,因此,单靠汽车来回接送无法使8人都赶上火车.
第二种情况:
若在汽车送第一批人的同时,其他人先步行,可以节省时间,汽车送完第一批人后,用了x
解:此题可分类讨论:
小时与第二批人相遇,再用x小时送到火车站,则列方程得,
解得:
所用时间为: 时,
因为40.4<42,因此,这时8人能赶上火车.
