2021—2022学年湘教版数学八年级上册2.4线段的垂直平分线(第1课时) 课件(19张)
文档属性
| 名称 | 2021—2022学年湘教版数学八年级上册2.4线段的垂直平分线(第1课时) 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 11:01:29 | ||
图片预览




文档简介
(共19张PPT)
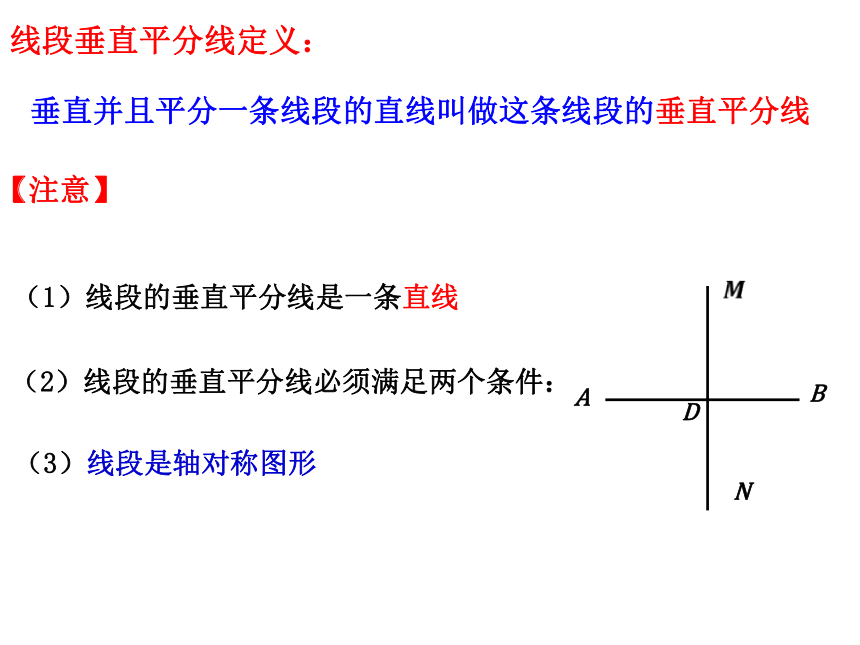
如图,A、B表示两个村庄,要在A、B一侧的河岸边建造一个自
来水厂,使它到两个村庄的距离相等,自来水厂应建在什么位置
A
B
你能想到办法吗?
2.4 线段的垂直平分线
第一课时
学习目标
1.理解线段垂直平分线的概念.
2.掌握线段的垂直平分线的性质,并会判断某点
是否在线段的垂直平分线上.
3.会用尺规作出已知线段的垂直平分线.
③线段AB是轴对称图形吗?
M
N
O
是
实验与探究(一)
动手做一做:在纸上做一条线段AB,通过对折使端点A与端点B重合.将纸展开后铺平,记折痕所在的直线为MN,直线MN与线段AB的交点为O.
OA=OB
MN⊥AB
思考:
①线段AO与BO的长度有什么有关系?
②直线MN与线段AB有怎样的位置关系?
A
B
N
D
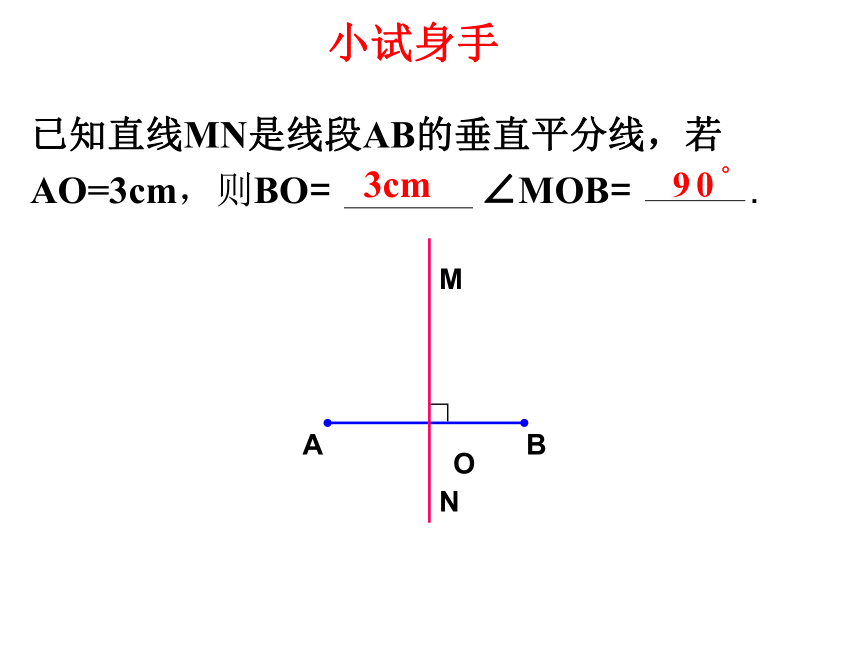
垂直并且平分一条线段的直线叫做这条线段的垂直平分线
线段垂直平分线定义:
【注意】
(3)线段是轴对称图形
(1)线段的垂直平分线是一条直线
(2)线段的垂直平分线必须满足两个条件:
已知直线MN是线段AB的垂直平分线,若
AO=3cm,则BO= ∠MOB= .
A
B
∟
M
N
O
3cm
小试身手
M
O
N
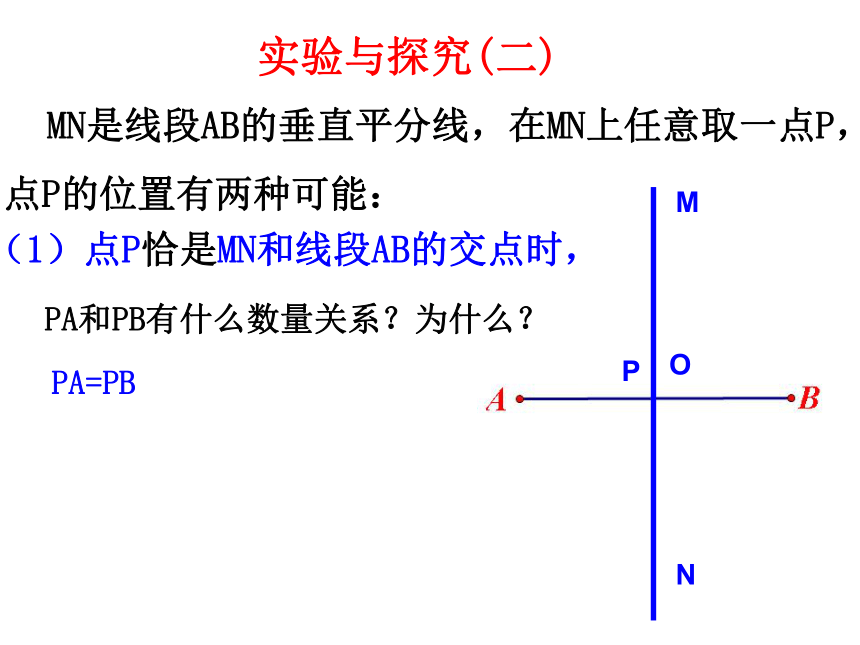
MN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:
(1)点P恰是MN和线段AB的交点时,
P
PA和PB有什么数量关系?为什么?
PA=PB
实验与探究(二)
M
N
(2)点P 不在线段AB上时,
P
PA=PB
MN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:
PA和PB有什么数量关系?为什么?
综合(1)(2)可得,
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等
线段垂直平分线上的点到线段两端的距离相等.
∵点P在线段AB的垂直平分线上
∴PA=PB
P
A
B
∟
线段垂直平分线的性质:
此性质可用来判定两条线段相等
总结
几何语言:
如图,线段AB被直线MN垂直平分,图中有哪些相等的线段
AD=BD
AP=BP
AC=BC
AO=BO
小试身手
已知:如图,直线DE是线段AB的垂直平分线,如果AC=4,BC=2,那么△BCE的周长等于 .
6
小组合作:先独立思考2分钟,再小组合作交流2分钟.
我来挑战
实验与探究(三)
思考:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
A
B
(1)当点P在线段AB上时,
∵PA=PB,
∴点P是AB的中点,
此时点P在线段AB的垂直平分线上.
·
P
实验与探究(三)
思考:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
(2)当点P在线段AB外时,PA=PB
设线段AB的中点为O,则OA=OB.
连接PO,由SSS可知△POA ≌△POB .
因为∠AOP+∠BOP=180°,∠AOP =∠BOP,
所以∠AOP = 90°,即 PO⊥ AB .
所以PO就是线段AB的垂直平分线,
即点P在线段AB的垂直平分线上.
到线段两端距离相等的点在线段的垂直平分线上.
∵ PA=PB
∴点P在线段AB的垂直平分线上
文字语言
符号语言
P
A
B
∟
线段垂直平分线的判定:
o
M
N
如图,已知线段AB,你能作出线段AB的垂直平分线吗?
A
B
C
D
作法:
(2)作直线CD;
CD即为所求的直线.
尺规作图
(1)分别以点A、B为圆心,以
大于 AB的长为半径作弧,两
弧相交于C、D两点;
如图,A、B表示两个村庄,要在A、B一侧的河岸边建造一个自
来水厂,使它到两个村庄的距离相等,自来水厂应建在什么位置
A
B
你能想到办法吗?
如图,A、B表示两个村庄,要在A、B一侧的河岸边建造一个自来水厂,使它到两个村庄的距离相等,自来水厂应建在什么位置
A
B
C
我已经想到办法了!
∟
线段的垂直平分线
线段的垂直平分线的定义.
线段的垂直平分线的性质.
线段的垂直平分线的判定.
用尺规作出已知线段的垂直平分线.
课堂小结
作业
如图,A、B表示两个村庄,要在A、B一侧的河岸边建造一个自
来水厂,使它到两个村庄的距离相等,自来水厂应建在什么位置
A
B
你能想到办法吗?
2.4 线段的垂直平分线
第一课时
学习目标
1.理解线段垂直平分线的概念.
2.掌握线段的垂直平分线的性质,并会判断某点
是否在线段的垂直平分线上.
3.会用尺规作出已知线段的垂直平分线.
③线段AB是轴对称图形吗?
M
N
O
是
实验与探究(一)
动手做一做:在纸上做一条线段AB,通过对折使端点A与端点B重合.将纸展开后铺平,记折痕所在的直线为MN,直线MN与线段AB的交点为O.
OA=OB
MN⊥AB
思考:
①线段AO与BO的长度有什么有关系?
②直线MN与线段AB有怎样的位置关系?
A
B
N
D
垂直并且平分一条线段的直线叫做这条线段的垂直平分线
线段垂直平分线定义:
【注意】
(3)线段是轴对称图形
(1)线段的垂直平分线是一条直线
(2)线段的垂直平分线必须满足两个条件:
已知直线MN是线段AB的垂直平分线,若
AO=3cm,则BO= ∠MOB= .
A
B
∟
M
N
O
3cm
小试身手
M
O
N
MN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:
(1)点P恰是MN和线段AB的交点时,
P
PA和PB有什么数量关系?为什么?
PA=PB
实验与探究(二)
M
N
(2)点P 不在线段AB上时,
P
PA=PB
MN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:
PA和PB有什么数量关系?为什么?
综合(1)(2)可得,
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等
线段垂直平分线上的点到线段两端的距离相等.
∵点P在线段AB的垂直平分线上
∴PA=PB
P
A
B
∟
线段垂直平分线的性质:
此性质可用来判定两条线段相等
总结
几何语言:
如图,线段AB被直线MN垂直平分,图中有哪些相等的线段
AD=BD
AP=BP
AC=BC
AO=BO
小试身手
已知:如图,直线DE是线段AB的垂直平分线,如果AC=4,BC=2,那么△BCE的周长等于 .
6
小组合作:先独立思考2分钟,再小组合作交流2分钟.
我来挑战
实验与探究(三)
思考:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
A
B
(1)当点P在线段AB上时,
∵PA=PB,
∴点P是AB的中点,
此时点P在线段AB的垂直平分线上.
·
P
实验与探究(三)
思考:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
(2)当点P在线段AB外时,PA=PB
设线段AB的中点为O,则OA=OB.
连接PO,由SSS可知△POA ≌△POB .
因为∠AOP+∠BOP=180°,∠AOP =∠BOP,
所以∠AOP = 90°,即 PO⊥ AB .
所以PO就是线段AB的垂直平分线,
即点P在线段AB的垂直平分线上.
到线段两端距离相等的点在线段的垂直平分线上.
∵ PA=PB
∴点P在线段AB的垂直平分线上
文字语言
符号语言
P
A
B
∟
线段垂直平分线的判定:
o
M
N
如图,已知线段AB,你能作出线段AB的垂直平分线吗?
A
B
C
D
作法:
(2)作直线CD;
CD即为所求的直线.
尺规作图
(1)分别以点A、B为圆心,以
大于 AB的长为半径作弧,两
弧相交于C、D两点;
如图,A、B表示两个村庄,要在A、B一侧的河岸边建造一个自
来水厂,使它到两个村庄的距离相等,自来水厂应建在什么位置
A
B
你能想到办法吗?
如图,A、B表示两个村庄,要在A、B一侧的河岸边建造一个自来水厂,使它到两个村庄的距离相等,自来水厂应建在什么位置
A
B
C
我已经想到办法了!
∟
线段的垂直平分线
线段的垂直平分线的定义.
线段的垂直平分线的性质.
线段的垂直平分线的判定.
用尺规作出已知线段的垂直平分线.
课堂小结
作业
同课章节目录
