2.6.1 应用一元二次方程(1) 课件(共32张PPT)
文档属性
| 名称 | 2.6.1 应用一元二次方程(1) 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 887.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:09:53 | ||
图片预览











文档简介
(共32张PPT)
2.6.1应用一元二次方程(1)
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.使学生会用一元二次方程解应用题.
2.进一步培养学生将实际问题转化为数学问题的能力和分析问题、解决问题的能力,培养学生运用数学的意识.
3.通过列方程解应用题,进一步体会运用代数中方程的思想方法解应用题的优越性.
导入新课
列方程解应用题的一般步骤是:
1.审:审清题意,找等量关系
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的解;是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
列方程解应用题的关键是: 找出相等关系
利用一元二次方程解决几何问题
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(1)如果梯子的顶端下滑1m,那梯子的底端滑动多少米?
解:由勾股定理知,滑动前梯子底端距墙6 m
设梯子底端滑动x m,那么滑动后梯子底端距墙(6+x)m
72+(x+6)2=102
探究新知
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(2)梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
(8-x)2+(x+6)2=102
设梯子顶端下滑x m,梯子底端滑动(6+x)m,得
解:由勾股定理知,滑动前梯子底端距墙6 m
探究新知
本章开始时梯子下滑的问题:.
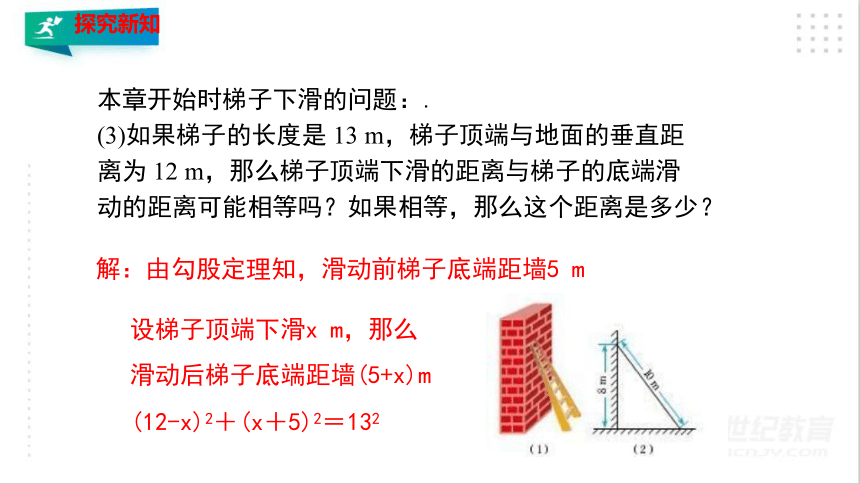
(3)如果梯子的长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
(12-x)2+(x+5)2=132
设梯子顶端下滑x m,那么滑动后梯子底端距墙(5+x)m
解:由勾股定理知,滑动前梯子底端距墙5 m
探究新知
例1 :如图,某海军基地位于A处,在其正南方向200n mile 处有一目标B,在B的正东方向200n mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
东
北
A
B
C
D
F
例题讲解
(1)小岛D与小岛F相距多少海里
东
北
A
B
C
D
F
解:连接DF.∵AD=CD , BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF= AB,
∵AB⊥BC, AB = BC =200n mile,
∴DF⊥BC, DF =100n mile.
例题讲解
东
北
A
B
C
D
F
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
E
解: 设相遇是补给船航行了x n mile,那么
DE = x n mile , AE + BE = 2x n mile,
EF=AB +BF-(AB + BE) =(300 - 2x)n mile.
在Rt△DEF中,根据勾股定理可得方程
x2 = 1002 + (300 - 2x)2.
整理得: 3x2 - 1200x + 100000 = 0 ,
解方程得 (舍去)
例题讲解
该部分是学习中的难点,要去审清题意,分析各量之间的关系,不能粗线条解决.在讲解过程中可逐步分解难点:
①审清题意;
②找准各条有关线段的长度关系;
③建立方程模型,之后求解.
与直角三角形有关的问题:直角三角形两直角边的平方和等于斜边的平方是这类问题的等量关系,即用勾股定理列方程.
总结归纳
利用一元二次方程解决动点问题
如图,A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P,Q两点从出发开始到几秒?
四边形PBCQ的面积为33cm2;
(2)P,Q两点从出发开始到几秒时?
点P和点Q的距离是10cm.
探究新知
解:(1)设P,Q两点运动x秒时四边形PBCQ的面积为33cm2,
则PB=(16-3x)cm,QC=2x cm.根据梯形的面积
公式得 (16-3x+2x)×6=33,解得x=5.
(2)设P,Q两点从出发经过t秒时,
点P,Q间的距离是10cm,
如图,作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10.∵PA=3t,CQ=BE=2t,
∴PE=AB-AP-BE= |16-5t| .
由勾股定理,得(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P,Q两点从出发开始到5秒时四边形PBCQ的面积为33 cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10 cm.
探究新知
解:设x秒后,△ PCQ的面积是Rt △ABC面积的一半.根据题意
整理,得 x2 - 14x + 24 = 0.
解方程,得 x1 = 2 , x2 = 12 (不符题意,舍去).
答:2秒后,△ PCQ的面积是Rt △ABC面积的一半.
如图,在Rt△ABC中,∠C=90°,点P,Q同时由A,B两点出发,分别沿AC,BC方向向点C匀速移动(到点C为止),它们的速度都是1m/s.几秒后△PCQ的面积是Rt△ACB面积的一半
A
B
C
P
Q
8m
6m
例题讲解
如图,在矩形ABCD中,AB=6cm, BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
A
B
C
D
Q
P
解:设所需时间为 t s,根据题意,得
2t (6 - t) ÷2 = 6×12 - 64.
整理得 t2 - 6t + 8 = 0.
解方程,得 t1 = 2 , t2 = 4 .
答:在第2秒和第4秒是五边形面积是 64cm2.
(6 - t)
2t
例题讲解
1)关键—— 动中取静
把动的点进行转换,变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;
由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.
3)常找的数量关系——面积,勾股定理,相似三角形等;
方法归纳
动点问题
利用一元二次方程解决面积问题
1.某校为了美化校园,准备在一块长32m,宽20m的长方形场地上修筑若干条宽度相同的道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少 使图(1),(2)的草坪面积为540m2.
(1)
(2)
探究新知
解:(1)如图,设道路的宽为xm,则
化简得,
其中的 x=25超出了原矩形的宽,应舍去.
答:图(1)中道路的宽为1m.
(1)
(32-2x)(20-2x)=540
探究新知
横向路面:
(2)如图,设路宽为xm,
32xm2
纵向路面面积为:
20xm2
草坪矩形的长(横向)为:
草坪矩形的宽(纵向:)为:
相等关系是:草坪长×草坪宽=540m2
(20-x)m
(32-x)m
即
化简得:
再往下的计算、格式书写与解法一相同.
(2)
探究新知
在这类问题中,一般依据几何图形的性质(如熟记特殊图形的面积公式),通过寻求面积的增加(或减少),将不规则的图形分割成或组合成规则图形等来寻找问题中的等量关系。
几何图形的面积问题
方法归纳
常见的图形有下列几种:
1.用长为100cm的金属丝制成一个矩形框子,框子的面积不可能是( )
A.375cm2 B.500cm2
C.625cm2 D.700cm2
D
课堂练习
2.一块矩形耕地大小尺寸如图所示,要在这块耕地上沿东西和南北方向分别挖两条和四条水渠,如果水渠的宽相等,而且要保证余下的可耕地面积为9600m2,那么水渠的宽为( )
A.2m B.4m
C.1m D.3m
C
课堂练习
3. 如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm. 动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动. 下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A. 第2秒钟 B. 第3秒钟
C. 第4秒钟 D. 第5秒钟
B
课堂练习
4. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
80cm
x
x
x
x
50cm
B
课堂练习
5.《九章算术》“勾股”章中有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何 ”
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙
的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向
走了一段后与乙相遇.那么相遇时,甲,乙各走了多远
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x - 10)2 = (3x) 2 +10 2.
整理得 2x2 - 7x = 0.
解方程,得 x1=3.5, x2=0 (不合题意,舍去).
∴3x=3×3.5 =10.5 , 7x = 7×3.5 = 24.5.
答:甲走了24.5步,乙走了10.5步.
O
东
北
A
B
10
3x
7x -10
课堂练习
6. 如图1,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540平方米,求道路的宽.
解:设道路宽为x米,由平移得到图2,则宽为(20-x)米,长为(32-x)米,列方程得
(20-x)(32-x)=540,
整理得 x2-52x+100=0,
解得 x1=50(舍去),x2=2.
答:道路宽为2米.
图1
图2
课堂练习
7.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
解:设该矩形草坪BC边的长为x,则
得x1=20(舍去),x2=12.
∴该矩形草坪BC边长为12米.
课堂练习
8.如图,在矩形ABCD中,DC=14cm,AD=6cm,动点P从点A出发,以4cm/s的速度沿A→B方向向点B运动,动点Q从点C出发,以1cm/s的速度沿C→D方向向点D运动,两点同时出发,一点到达终点时另一点即停,设运动时间为t(s),求t为何值时,点P和点Q之间的距离是10cm.
课堂练习
解:过点P作PE⊥CD于点E,
则PE=AD=6cm,EQ=|14﹣4t﹣t|cm,
如图所示.
依题意,得:62+|14﹣4t﹣t|2=102,
整理,得: 25t2﹣140t+132=0,
解得:t1= ,t2= .
当t= 时,4t= >14,不合题意,舍去.
答:当t为 秒时,点P和点Q之间的距离是10cm.
课堂练习
课堂小结
利用一元二次方程
解决行程问题
列方程步骤:
应用类型
几何问题
面积问题
动点问题
审
设
列
解
检
答
https://www.21cnjy.com/help/help_extract.php
2.6.1应用一元二次方程(1)
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.使学生会用一元二次方程解应用题.
2.进一步培养学生将实际问题转化为数学问题的能力和分析问题、解决问题的能力,培养学生运用数学的意识.
3.通过列方程解应用题,进一步体会运用代数中方程的思想方法解应用题的优越性.
导入新课
列方程解应用题的一般步骤是:
1.审:审清题意,找等量关系
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的解;是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
列方程解应用题的关键是: 找出相等关系
利用一元二次方程解决几何问题
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(1)如果梯子的顶端下滑1m,那梯子的底端滑动多少米?
解:由勾股定理知,滑动前梯子底端距墙6 m
设梯子底端滑动x m,那么滑动后梯子底端距墙(6+x)m
72+(x+6)2=102
探究新知
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(2)梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
(8-x)2+(x+6)2=102
设梯子顶端下滑x m,梯子底端滑动(6+x)m,得
解:由勾股定理知,滑动前梯子底端距墙6 m
探究新知
本章开始时梯子下滑的问题:.
(3)如果梯子的长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
(12-x)2+(x+5)2=132
设梯子顶端下滑x m,那么滑动后梯子底端距墙(5+x)m
解:由勾股定理知,滑动前梯子底端距墙5 m
探究新知
例1 :如图,某海军基地位于A处,在其正南方向200n mile 处有一目标B,在B的正东方向200n mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
东
北
A
B
C
D
F
例题讲解
(1)小岛D与小岛F相距多少海里
东
北
A
B
C
D
F
解:连接DF.∵AD=CD , BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF= AB,
∵AB⊥BC, AB = BC =200n mile,
∴DF⊥BC, DF =100n mile.
例题讲解
东
北
A
B
C
D
F
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
E
解: 设相遇是补给船航行了x n mile,那么
DE = x n mile , AE + BE = 2x n mile,
EF=AB +BF-(AB + BE) =(300 - 2x)n mile.
在Rt△DEF中,根据勾股定理可得方程
x2 = 1002 + (300 - 2x)2.
整理得: 3x2 - 1200x + 100000 = 0 ,
解方程得 (舍去)
例题讲解
该部分是学习中的难点,要去审清题意,分析各量之间的关系,不能粗线条解决.在讲解过程中可逐步分解难点:
①审清题意;
②找准各条有关线段的长度关系;
③建立方程模型,之后求解.
与直角三角形有关的问题:直角三角形两直角边的平方和等于斜边的平方是这类问题的等量关系,即用勾股定理列方程.
总结归纳
利用一元二次方程解决动点问题
如图,A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P,Q两点从出发开始到几秒?
四边形PBCQ的面积为33cm2;
(2)P,Q两点从出发开始到几秒时?
点P和点Q的距离是10cm.
探究新知
解:(1)设P,Q两点运动x秒时四边形PBCQ的面积为33cm2,
则PB=(16-3x)cm,QC=2x cm.根据梯形的面积
公式得 (16-3x+2x)×6=33,解得x=5.
(2)设P,Q两点从出发经过t秒时,
点P,Q间的距离是10cm,
如图,作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10.∵PA=3t,CQ=BE=2t,
∴PE=AB-AP-BE= |16-5t| .
由勾股定理,得(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P,Q两点从出发开始到5秒时四边形PBCQ的面积为33 cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10 cm.
探究新知
解:设x秒后,△ PCQ的面积是Rt △ABC面积的一半.根据题意
整理,得 x2 - 14x + 24 = 0.
解方程,得 x1 = 2 , x2 = 12 (不符题意,舍去).
答:2秒后,△ PCQ的面积是Rt △ABC面积的一半.
如图,在Rt△ABC中,∠C=90°,点P,Q同时由A,B两点出发,分别沿AC,BC方向向点C匀速移动(到点C为止),它们的速度都是1m/s.几秒后△PCQ的面积是Rt△ACB面积的一半
A
B
C
P
Q
8m
6m
例题讲解
如图,在矩形ABCD中,AB=6cm, BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
A
B
C
D
Q
P
解:设所需时间为 t s,根据题意,得
2t (6 - t) ÷2 = 6×12 - 64.
整理得 t2 - 6t + 8 = 0.
解方程,得 t1 = 2 , t2 = 4 .
答:在第2秒和第4秒是五边形面积是 64cm2.
(6 - t)
2t
例题讲解
1)关键—— 动中取静
把动的点进行转换,变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;
由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.
3)常找的数量关系——面积,勾股定理,相似三角形等;
方法归纳
动点问题
利用一元二次方程解决面积问题
1.某校为了美化校园,准备在一块长32m,宽20m的长方形场地上修筑若干条宽度相同的道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少 使图(1),(2)的草坪面积为540m2.
(1)
(2)
探究新知
解:(1)如图,设道路的宽为xm,则
化简得,
其中的 x=25超出了原矩形的宽,应舍去.
答:图(1)中道路的宽为1m.
(1)
(32-2x)(20-2x)=540
探究新知
横向路面:
(2)如图,设路宽为xm,
32xm2
纵向路面面积为:
20xm2
草坪矩形的长(横向)为:
草坪矩形的宽(纵向:)为:
相等关系是:草坪长×草坪宽=540m2
(20-x)m
(32-x)m
即
化简得:
再往下的计算、格式书写与解法一相同.
(2)
探究新知
在这类问题中,一般依据几何图形的性质(如熟记特殊图形的面积公式),通过寻求面积的增加(或减少),将不规则的图形分割成或组合成规则图形等来寻找问题中的等量关系。
几何图形的面积问题
方法归纳
常见的图形有下列几种:
1.用长为100cm的金属丝制成一个矩形框子,框子的面积不可能是( )
A.375cm2 B.500cm2
C.625cm2 D.700cm2
D
课堂练习
2.一块矩形耕地大小尺寸如图所示,要在这块耕地上沿东西和南北方向分别挖两条和四条水渠,如果水渠的宽相等,而且要保证余下的可耕地面积为9600m2,那么水渠的宽为( )
A.2m B.4m
C.1m D.3m
C
课堂练习
3. 如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm. 动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动. 下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A. 第2秒钟 B. 第3秒钟
C. 第4秒钟 D. 第5秒钟
B
课堂练习
4. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
80cm
x
x
x
x
50cm
B
课堂练习
5.《九章算术》“勾股”章中有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何 ”
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙
的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向
走了一段后与乙相遇.那么相遇时,甲,乙各走了多远
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x - 10)2 = (3x) 2 +10 2.
整理得 2x2 - 7x = 0.
解方程,得 x1=3.5, x2=0 (不合题意,舍去).
∴3x=3×3.5 =10.5 , 7x = 7×3.5 = 24.5.
答:甲走了24.5步,乙走了10.5步.
O
东
北
A
B
10
3x
7x -10
课堂练习
6. 如图1,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540平方米,求道路的宽.
解:设道路宽为x米,由平移得到图2,则宽为(20-x)米,长为(32-x)米,列方程得
(20-x)(32-x)=540,
整理得 x2-52x+100=0,
解得 x1=50(舍去),x2=2.
答:道路宽为2米.
图1
图2
课堂练习
7.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
解:设该矩形草坪BC边的长为x,则
得x1=20(舍去),x2=12.
∴该矩形草坪BC边长为12米.
课堂练习
8.如图,在矩形ABCD中,DC=14cm,AD=6cm,动点P从点A出发,以4cm/s的速度沿A→B方向向点B运动,动点Q从点C出发,以1cm/s的速度沿C→D方向向点D运动,两点同时出发,一点到达终点时另一点即停,设运动时间为t(s),求t为何值时,点P和点Q之间的距离是10cm.
课堂练习
解:过点P作PE⊥CD于点E,
则PE=AD=6cm,EQ=|14﹣4t﹣t|cm,
如图所示.
依题意,得:62+|14﹣4t﹣t|2=102,
整理,得: 25t2﹣140t+132=0,
解得:t1= ,t2= .
当t= 时,4t= >14,不合题意,舍去.
答:当t为 秒时,点P和点Q之间的距离是10cm.
课堂练习
课堂小结
利用一元二次方程
解决行程问题
列方程步骤:
应用类型
几何问题
面积问题
动点问题
审
设
列
解
检
答
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
