2021-2022学年数学人教A版(2019)必修第一册3.1.2椭圆的简单几何性质 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册3.1.2椭圆的简单几何性质 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
一、温故知新
1、椭圆的标准方程
二、新知探究
观察
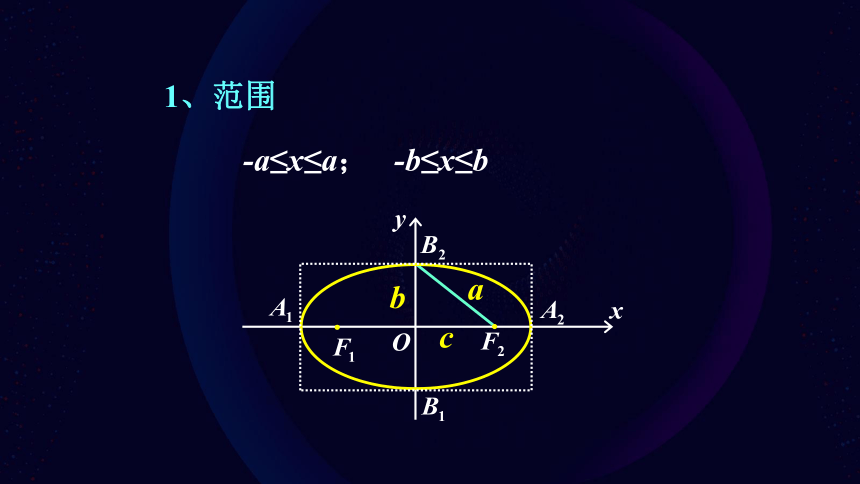
1、范围
-a≤x≤a; -b≤x≤b
2、对称性
椭圆图像关于什么对称?
3、顶点
探究
A1(-a, 0)、A2(a, 0) B1(0, -b)、B2(0, b)
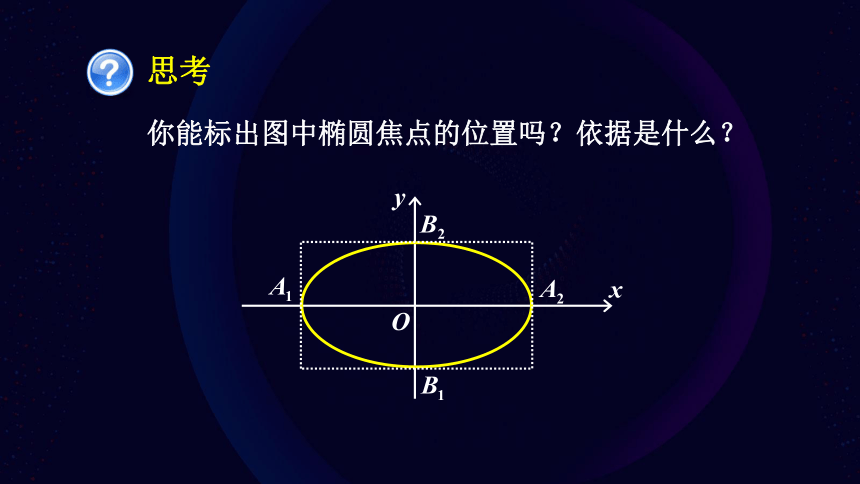
你能标出图中椭圆焦点的位置吗?依据是什么?
思考
你能标出图中椭圆焦点的位置吗?依据是什么?
思考
4、离心率
思考
4、离心率
探究
【例1】
【例2】
【例3】
【例4】
若椭圆上存在三点,使得这三点与椭圆中心恰好是一个正方形的四个顶点,则该椭圆的离心率为 ( )
【例5】
1. 范围、对称性、顶点是刻画椭圆形状、大小和位置的简单几何性质,椭圆的大致图形一般由这几个性质确定.
2. 椭圆的离心率是反映椭圆扁平程度的一个几何性质, 它能换算为a,b,c任意两个数之间的直接关系,也是确定椭圆的一个基本条件,在解题中会经常遇到.
三、课堂小结
《课后作业》
第2课时
四、作业布置
【例1】
五、作业补充
【例2】
【例3】如图, 一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上.
由椭圆一个焦点F1发出的光线,
经过旋转椭圆面反射后集中到
另一个焦点F2. 已知BC⊥F1F2,
|F1B|=2.8cm, |F1F2|=4.5cm, 试
建立适当的坐标系, 求截口BAC
所在椭圆的方程.
一、温故知新
1、椭圆的标准方程
二、新知探究
观察
1、范围
-a≤x≤a; -b≤x≤b
2、对称性
椭圆图像关于什么对称?
3、顶点
探究
A1(-a, 0)、A2(a, 0) B1(0, -b)、B2(0, b)
你能标出图中椭圆焦点的位置吗?依据是什么?
思考
你能标出图中椭圆焦点的位置吗?依据是什么?
思考
4、离心率
思考
4、离心率
探究
【例1】
【例2】
【例3】
【例4】
若椭圆上存在三点,使得这三点与椭圆中心恰好是一个正方形的四个顶点,则该椭圆的离心率为 ( )
【例5】
1. 范围、对称性、顶点是刻画椭圆形状、大小和位置的简单几何性质,椭圆的大致图形一般由这几个性质确定.
2. 椭圆的离心率是反映椭圆扁平程度的一个几何性质, 它能换算为a,b,c任意两个数之间的直接关系,也是确定椭圆的一个基本条件,在解题中会经常遇到.
三、课堂小结
《课后作业》
第2课时
四、作业布置
【例1】
五、作业补充
【例2】
【例3】如图, 一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上.
由椭圆一个焦点F1发出的光线,
经过旋转椭圆面反射后集中到
另一个焦点F2. 已知BC⊥F1F2,
|F1B|=2.8cm, |F1F2|=4.5cm, 试
建立适当的坐标系, 求截口BAC
所在椭圆的方程.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
