2.1.2 指数函数及其性质 课件(共21张PPT)2021-2022学年高一上学期 人教A版 数学必修1
文档属性
| 名称 | 2.1.2 指数函数及其性质 课件(共21张PPT)2021-2022学年高一上学期 人教A版 数学必修1 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 11:07:17 | ||
图片预览








文档简介
(共21张PPT)
2.1.2
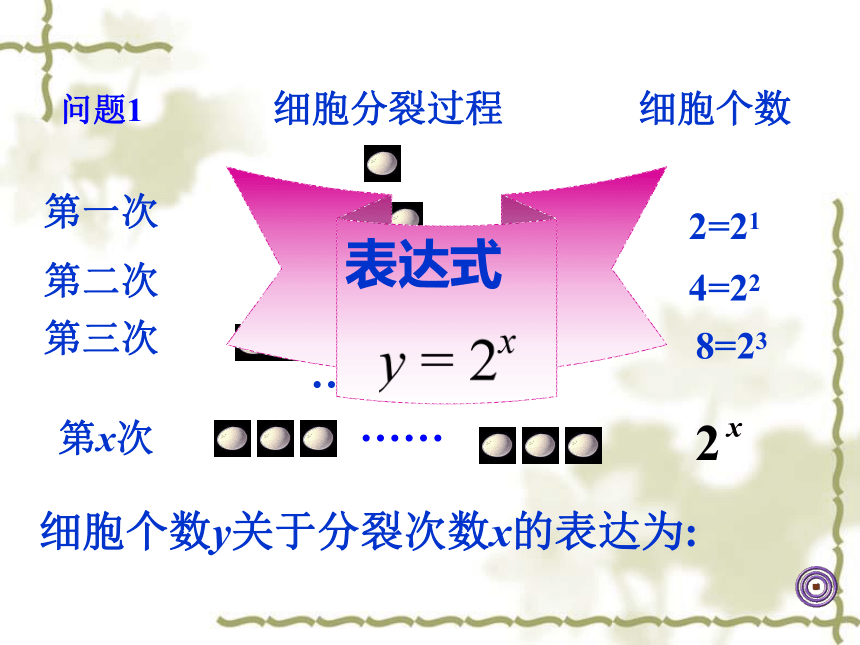
问题1.某种细胞分裂时,由1个分裂成2个,2个 分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是什么?
问题1
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达为:
表达式
问题2:认真观察并回答下列问题:
(1).一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是:
(2).一根1米长的绳子从中间剪一次剩下 米,再从中
间剪一次剩下 米,若这条绳子剪x次剩下y米,
则y与x的函数关系是:
我们把这种自变量在指数位置上而底数是一
个大于0且不等于1的常量的函数叫做指数函数.
1指数函数的定义:
函数
叫做指数函数,其中x是自变量,
在
中指数x是自变量,
底数是一个大于0且不等于1的常量.
定义域是R。
探究1:为什么要规定
(1)若
则当x > 0时,
当x≤0时,
无意义.
(2)若
则对于x的某些数值,可使
无意义.
在实数范围内函数值不存在.
(3)若
则对于任何
是一个常量,没有研究的必要性
如
,这时对于
……等等,
探讨:若不满足上述条件
会怎么样
探究2:函数 是指数函数吗?
有些函数貌似指数函数,实际上却不是.
指数函数的解析式 中, 的系数是1.
有些函数看起来不像指数函数,实际上却是.
练习:
1.下列函数是指数函数的是 ( )
A. y=(-3)x B. y=3x+1 C. y=-3x+1 D. y=3-x
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
D
2.指数函数的图象和性质:
在同一坐标系中分别作出函数的图象.
指数函数的图象和性质:
在同一坐标系中分别作出如下函数的图像:
列表如下:
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… 0.13 0.25 0.5 0.71 1 1.4 2 4 8 …
… 8 4 2 1.4 1 0.71 0.5 0.25 0.13 …
x … -1.5 -1 -0.5 -0.25 0 0.25 0.5 1 1.5 …
… 0.03 0.1 0.32 0.56 1 1.78 3.16 10 31.62 …
… 31.62 10 3.16 1.78 1 0.56 0.32 0.1 0.03 …
-1
1 2 3
-3 -2 -1
4
3
2
1
0
y
x
y=2x
a>1 0图
象
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0x
y=1
y=ax
(0,1)
a>1 0图
象
特
征
a>1 0性
质
1.图象全在x轴上方,与x轴无限接近.
1.定义域为R,值域为(0,+ ).
2.图象过定点(0,1)
2.当x=0时,y=1
3.自左向右图象逐渐上升
3.自左向右图象逐渐下降
3.在R上是增函数
3.在R上是减函数
4.图象分布在左 下和右上两个区域内
4.图象分布在左上和右下两个区域内
4.当x>0时,y>1; 当x<0时,04.当x>0时, 01.
5.既不是奇函数又不是偶函数
0
1
x
y
试分析上述图像中,哪一条是 的图像
哪一条是 的图像
1
y=2x
y=3x
0
1
x
y
试分析上述图像中,哪一条是 的图像
哪一条是 的图像
y= (1/2)x
y=(1/3)x
指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0a>1
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,04.当x>0时, 01.
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
例2.求下列函数的定义域、值域:
函数的定义域为{x|x 0},
值域为{y |y>0 ,且y 1}.
解 (1)
(2)
函数的定义域为
2.指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0a>1
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,04.当x>0时, 01.
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
例3.比较下列各题中两个值的大小:
(1)1.52.5 ,1.5 3.2 ;
(2)0.5 – 1.2 ,0.5 – 1.5
(3)1.50.3 ,0.8 1.2
(1)考察指数函数y=1.5x .
由于底数1.5>1 ,所以指数函数
y=1.5x 在R上是增函数.
解:
∵2.5<3.2
∴1.52.5<1.53.2
(2)考察指数函数y=0.5x .
由于底数0<0.5<1 ,所以指数函数y=0.5x 在R上是减函数.
∵-1.2>-1.5
∴0.5-1.2<0.5-1.5
(3)由指数函数的性质知
1.50.3>1.5 0=1 ,
0.81.2<0.8 0=1 ,
∴1.5 0.3>0.8 1.2 .
2.指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0a>1
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,04.当x>0时, 01.
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
练习:
(1,+ )
(0, + )
[1, + )
(0,1]
(-1/2,0)
>
<
2.指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0a>1
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,04.当x>0时, 01.
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
练习:
y=ax(a>0且 a≠1)图象必过
点_______
2 y=ax-2(a>0且 a≠1)图象必
过点_______
y=ax+3-1(a>0且 a≠1)图象
必过点________
(0,1)
(2,1)
(-3,0)
4 某种细菌在培养过程中,每
20分钟分裂一次(一个分裂成
两个),经过3小时这种细菌
由一个分裂成______个
512
2.1.2
问题1.某种细胞分裂时,由1个分裂成2个,2个 分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是什么?
问题1
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达为:
表达式
问题2:认真观察并回答下列问题:
(1).一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是:
(2).一根1米长的绳子从中间剪一次剩下 米,再从中
间剪一次剩下 米,若这条绳子剪x次剩下y米,
则y与x的函数关系是:
我们把这种自变量在指数位置上而底数是一
个大于0且不等于1的常量的函数叫做指数函数.
1指数函数的定义:
函数
叫做指数函数,其中x是自变量,
在
中指数x是自变量,
底数是一个大于0且不等于1的常量.
定义域是R。
探究1:为什么要规定
(1)若
则当x > 0时,
当x≤0时,
无意义.
(2)若
则对于x的某些数值,可使
无意义.
在实数范围内函数值不存在.
(3)若
则对于任何
是一个常量,没有研究的必要性
如
,这时对于
……等等,
探讨:若不满足上述条件
会怎么样
探究2:函数 是指数函数吗?
有些函数貌似指数函数,实际上却不是.
指数函数的解析式 中, 的系数是1.
有些函数看起来不像指数函数,实际上却是.
练习:
1.下列函数是指数函数的是 ( )
A. y=(-3)x B. y=3x+1 C. y=-3x+1 D. y=3-x
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
D
2.指数函数的图象和性质:
在同一坐标系中分别作出函数的图象.
指数函数的图象和性质:
在同一坐标系中分别作出如下函数的图像:
列表如下:
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… 0.13 0.25 0.5 0.71 1 1.4 2 4 8 …
… 8 4 2 1.4 1 0.71 0.5 0.25 0.13 …
x … -1.5 -1 -0.5 -0.25 0 0.25 0.5 1 1.5 …
… 0.03 0.1 0.32 0.56 1 1.78 3.16 10 31.62 …
… 31.62 10 3.16 1.78 1 0.56 0.32 0.1 0.03 …
-1
1 2 3
-3 -2 -1
4
3
2
1
0
y
x
y=2x
a>1 0
象
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0
y=1
y=ax
(0,1)
a>1 0
象
特
征
a>1 0
质
1.图象全在x轴上方,与x轴无限接近.
1.定义域为R,值域为(0,+ ).
2.图象过定点(0,1)
2.当x=0时,y=1
3.自左向右图象逐渐上升
3.自左向右图象逐渐下降
3.在R上是增函数
3.在R上是减函数
4.图象分布在左 下和右上两个区域内
4.图象分布在左上和右下两个区域内
4.当x>0时,y>1; 当x<0时,0
5.既不是奇函数又不是偶函数
0
1
x
y
试分析上述图像中,哪一条是 的图像
哪一条是 的图像
1
y=2x
y=3x
0
1
x
y
试分析上述图像中,哪一条是 的图像
哪一条是 的图像
y= (1/2)x
y=(1/3)x
指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,0
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
例2.求下列函数的定义域、值域:
函数的定义域为{x|x 0},
值域为{y |y>0 ,且y 1}.
解 (1)
(2)
函数的定义域为
2.指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,0
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
例3.比较下列各题中两个值的大小:
(1)1.52.5 ,1.5 3.2 ;
(2)0.5 – 1.2 ,0.5 – 1.5
(3)1.50.3 ,0.8 1.2
(1)考察指数函数y=1.5x .
由于底数1.5>1 ,所以指数函数
y=1.5x 在R上是增函数.
解:
∵2.5<3.2
∴1.52.5<1.53.2
(2)考察指数函数y=0.5x .
由于底数0<0.5<1 ,所以指数函数y=0.5x 在R上是减函数.
∵-1.2>-1.5
∴0.5-1.2<0.5-1.5
(3)由指数函数的性质知
1.50.3>1.5 0=1 ,
0.81.2<0.8 0=1 ,
∴1.5 0.3>0.8 1.2 .
2.指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,0
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
练习:
(1,+ )
(0, + )
[1, + )
(0,1]
(-1/2,0)
>
<
2.指数函数的图象和性质
x
y
0
y=1
y=ax
(0,1)
y
0
x
y=ax
性
质
0
1.定义域为R,值域为(0,+ ).
2.过点(0,1)即x=0时,y=1
3.在R上是增函数
3.在R上是减函数
4.当x>0时,y>1;当x<0时,0
5.既不是奇函数也不是偶函数.
图 象
(0,1)
y=1
练习:
y=ax(a>0且 a≠1)图象必过
点_______
2 y=ax-2(a>0且 a≠1)图象必
过点_______
y=ax+3-1(a>0且 a≠1)图象
必过点________
(0,1)
(2,1)
(-3,0)
4 某种细菌在培养过程中,每
20分钟分裂一次(一个分裂成
两个),经过3小时这种细菌
由一个分裂成______个
512
