4.4.2对数函数的图像和性质课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共19张PPT)
文档属性
| 名称 | 4.4.2对数函数的图像和性质课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 947.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 11:08:05 | ||
图片预览




文档简介
(共19张PPT)
对数函数及其性质<一>
莒南一中 张芳
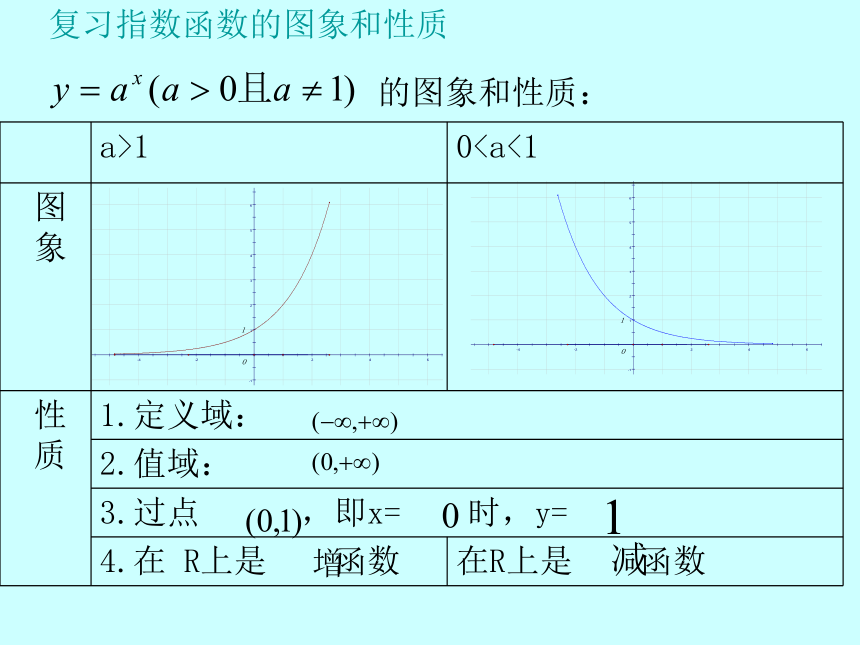
的图象和性质:
a>1 0图
象
性
质 1.定义域:
2.值域:
3.过点 ,即x= 时,y=
4.在 R上是 函数 在R上是 函数
复习指数函数的图象和性质
引例:当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约经过5730年衰减为原来的一半,这个时间称为”半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系:
考古学家通过提取附着在出土文物,古迹址生物体的残留物,利用 估算出出土文物或古遗址的年代.
对于任意个碳14的含量P,利用上式都有唯一确定的年代t与之对应,所以,t是P的函数.
新课讲解:
(一).对数函数的定义:
函数
叫做对数函数;
其中x是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:
(1)
(2)
2 对数函数对底数的限制:
且
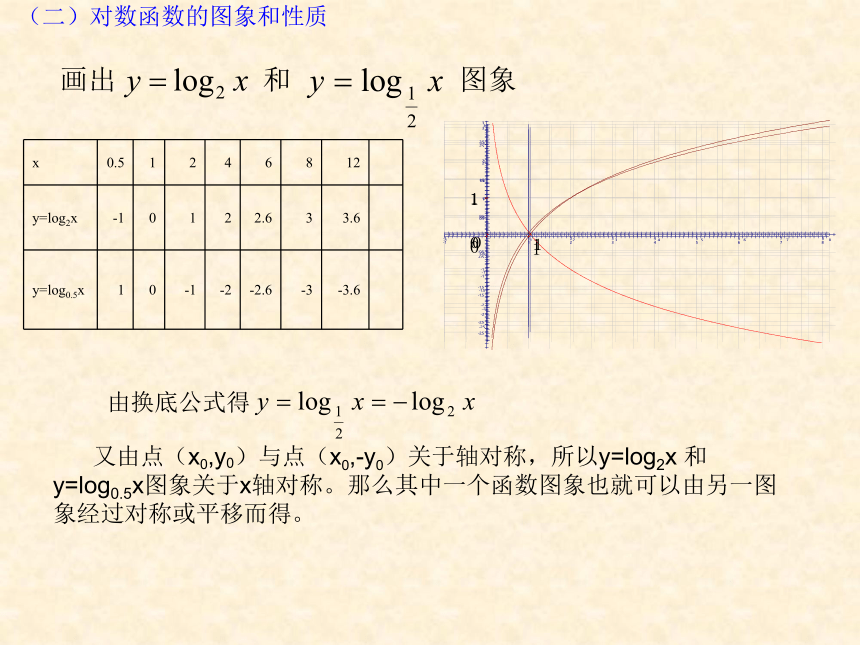
(二)对数函数的图象和性质
x 0.5 1 2 4 6 8 12
y=log2x -1 0 1 2 2.6 3 3.6
y=log0.5x 1 0 -1 -2 -2.6 -3 -3.6
图象
画出
和
又由点(x0,y0)与点(x0,-y0)关于轴对称,所以y=log2x 和 y=log0.5x图象关于x轴对称。那么其中一个函数图象也就可以由另一图象经过对称或平移而得。
由换底公式得
Ⅰ
Ⅱ
Ⅳ
Ⅲ
. 类比指数函数图象和性质的研究研究对数函数的性质:
思考底数a是如何影响函数 y=logax的呢
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
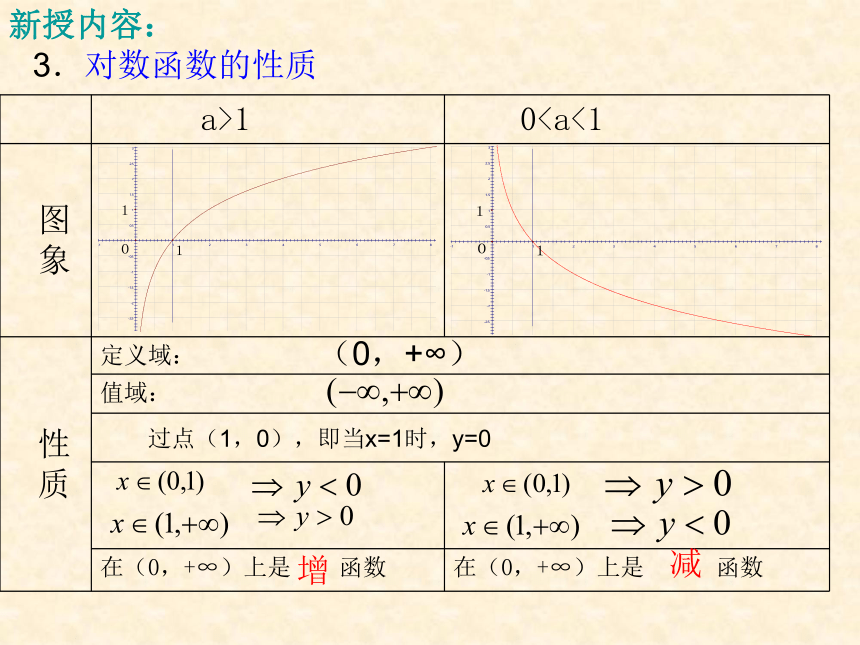
a>1 0图
象
性
质 定义域:
值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
新授内容:
3.对数函数的性质
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
例1求下列函数的定义域:
(1)
讲解范例
(2)
分析:求函数定义域时应从哪些方面来考虑?
解:(1)由4-x>0得x<4
所以函数的定义域为
(2)由 得
所以函数的定义域为
练习:(教材P73练习2).
例2
讲解范例
解(1):
解(2):
比较下列各组数中两个值的大小:
考查对数函数
因为它的底数2>1,所以它在
(0,+∞)上是增函数,于是
考查对数函数
因为它的底数0<0.3<1,所以它在
(0,+∞)上是减函数,于是
(1)
(2)
(3)
且
解(3): 当a>1时,以为函数y=logax在(0, +∞)上是增函数,且5.1<5.9,所以loga5.1当0loga5.9
(4)
(5)
分析(4):
(5):
方法总结:
(1)构造函数法。利用函数的单调性,适用于同底不同真。
(2)图像法。适用于同真不同底。
(3)搭桥法。适用于既不同底又不同真,常用的有-1,0,1 。
例3 解下列关于x的不等式:
(1) log0.5x > log0.5(1-x)
(2) log2(x+3) > 2
依据:
(3)
变式:
例4:求函数 y=log3x(1≤x≤3)的值域.
(1)已知函数y=logax(a>0,a≠1),
当x∈[3,9]时,函数的最大值比最小值大1,
则a=________
(2)求函数 y=log3(x2-4x+7)的值域.
小结 :
1.对数函数的定义:
函数
叫做对数函数;
的定义域为
值域为
小结 :
a>1 0图
象
性
质 定义域:
值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
2.对数函数的图象和性质
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
谢 谢!
对数函数模型(一)
火箭的最大速度v和燃料质量M、火箭质量m的函数关系是:
生物学家研究发现:洄游鱼类的游速v和鱼的耗氧量O之间的函数关系:
对数函数模型(二)
溶液的酸碱度是通过PH值来刻画的,PH值的计算公式为:
对数函数模型(三)
对数函数及其性质<一>
莒南一中 张芳
的图象和性质:
a>1 0
象
性
质 1.定义域:
2.值域:
3.过点 ,即x= 时,y=
4.在 R上是 函数 在R上是 函数
复习指数函数的图象和性质
引例:当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约经过5730年衰减为原来的一半,这个时间称为”半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系:
考古学家通过提取附着在出土文物,古迹址生物体的残留物,利用 估算出出土文物或古遗址的年代.
对于任意个碳14的含量P,利用上式都有唯一确定的年代t与之对应,所以,t是P的函数.
新课讲解:
(一).对数函数的定义:
函数
叫做对数函数;
其中x是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:
(1)
(2)
2 对数函数对底数的限制:
且
(二)对数函数的图象和性质
x 0.5 1 2 4 6 8 12
y=log2x -1 0 1 2 2.6 3 3.6
y=log0.5x 1 0 -1 -2 -2.6 -3 -3.6
图象
画出
和
又由点(x0,y0)与点(x0,-y0)关于轴对称,所以y=log2x 和 y=log0.5x图象关于x轴对称。那么其中一个函数图象也就可以由另一图象经过对称或平移而得。
由换底公式得
Ⅰ
Ⅱ
Ⅳ
Ⅲ
. 类比指数函数图象和性质的研究研究对数函数的性质:
思考底数a是如何影响函数 y=logax的呢
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
a>1 0
象
性
质 定义域:
值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
新授内容:
3.对数函数的性质
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
例1求下列函数的定义域:
(1)
讲解范例
(2)
分析:求函数定义域时应从哪些方面来考虑?
解:(1)由4-x>0得x<4
所以函数的定义域为
(2)由 得
所以函数的定义域为
练习:(教材P73练习2).
例2
讲解范例
解(1):
解(2):
比较下列各组数中两个值的大小:
考查对数函数
因为它的底数2>1,所以它在
(0,+∞)上是增函数,于是
考查对数函数
因为它的底数0<0.3<1,所以它在
(0,+∞)上是减函数,于是
(1)
(2)
(3)
且
解(3): 当a>1时,以为函数y=logax在(0, +∞)上是增函数,且5.1<5.9,所以loga5.1
(4)
(5)
分析(4):
(5):
方法总结:
(1)构造函数法。利用函数的单调性,适用于同底不同真。
(2)图像法。适用于同真不同底。
(3)搭桥法。适用于既不同底又不同真,常用的有-1,0,1 。
例3 解下列关于x的不等式:
(1) log0.5x > log0.5(1-x)
(2) log2(x+3) > 2
依据:
(3)
变式:
例4:求函数 y=log3x(1≤x≤3)的值域.
(1)已知函数y=logax(a>0,a≠1),
当x∈[3,9]时,函数的最大值比最小值大1,
则a=________
(2)求函数 y=log3(x2-4x+7)的值域.
小结 :
1.对数函数的定义:
函数
叫做对数函数;
的定义域为
值域为
小结 :
a>1 0
象
性
质 定义域:
值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
2.对数函数的图象和性质
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
谢 谢!
对数函数模型(一)
火箭的最大速度v和燃料质量M、火箭质量m的函数关系是:
生物学家研究发现:洄游鱼类的游速v和鱼的耗氧量O之间的函数关系:
对数函数模型(二)
溶液的酸碱度是通过PH值来刻画的,PH值的计算公式为:
对数函数模型(三)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
