第3章概率的进一步认识 达标测评 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第3章概率的进一步认识 达标测评 2021-2022学年北师大版九年级数学上册(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学上册《第3章概率的进一步认识》达标测评(附答案)
一.选择题(共12小题,满分48分)
1.某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )
A. B. C. D.
2.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
3.妙妙上学经过两个路口,如果每个路口可直接通过和需等待的可能性相等,那么妙妙上学时在这两个路口都直接通过的概率是( )
A. B. C. D.
4.为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )
A. B. C. D.
5.在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )
A. B. C. D.
6.如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
A. B. C. D.
7.为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下:
身高x/cm x<160 160≤x<170 170≤x<180 x≥180
人数 60 260 550 130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于170cm的概率是( )A.0.32 B.0.55 C.0.68 D.0.87
8.如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2 B.7m2 C.8m2 D.9m2
9.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5 B.10 C.12 D.15
10.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球试验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个 B.4个 C.18个 D.16个
11.在一个不透明的袋子里装有若干个白球和6个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有( )
A.2个 B.4个 C.14个 D.18个
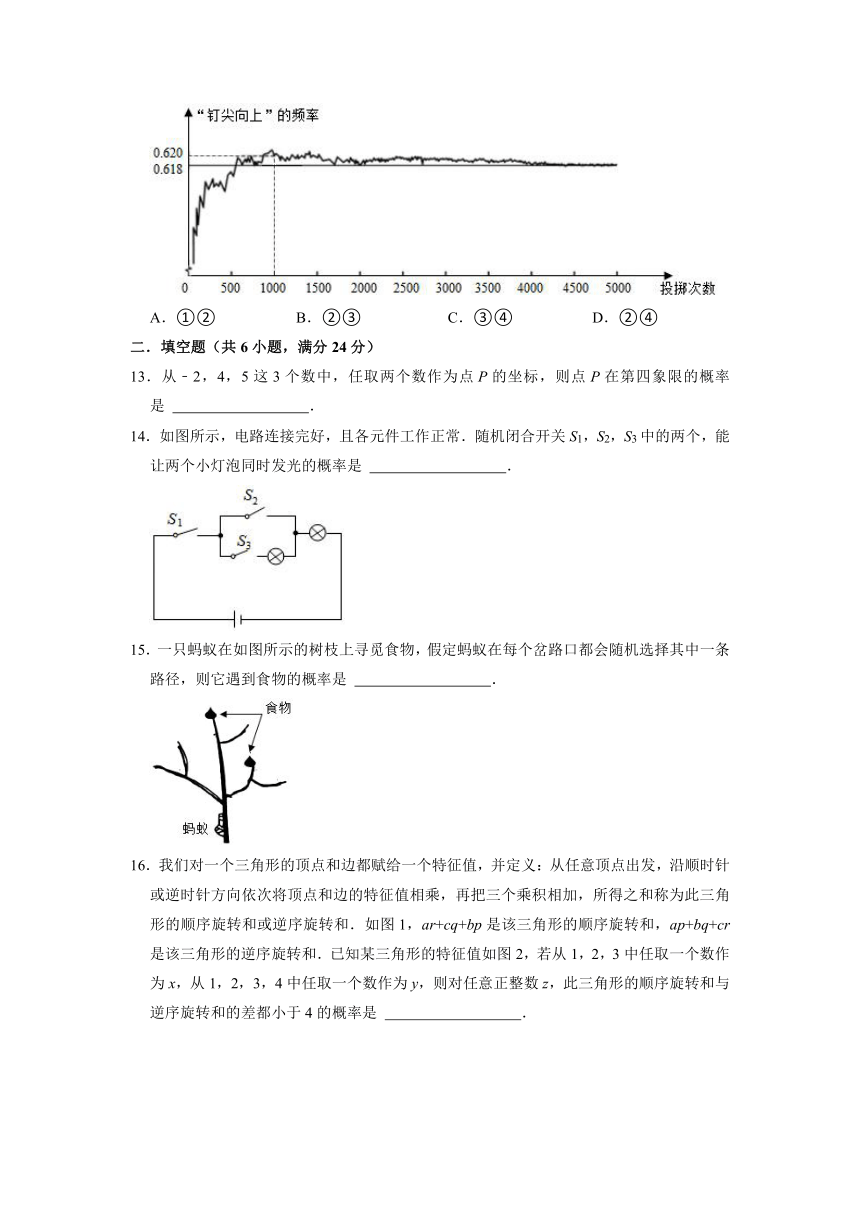
12.如图,显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.下面有四个推断:①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③当投掷次数是5000时,“钉尖向上”的频率不一定是0.618;④若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.其中合理的是( )
A.①② B.②③ C.③④ D.②④
二.填空题(共6小题,满分24分)
13.从﹣2,4,5这3个数中,任取两个数作为点P的坐标,则点P在第四象限的概率是 .
14.如图所示,电路连接完好,且各元件工作正常.随机闭合开关S1,S2,S3中的两个,能让两个小灯泡同时发光的概率是 .
15.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中一条路径,则它遇到食物的概率是 .
16.我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和.如图1,ar+cq+bp是该三角形的顺序旋转和,ap+bq+cr是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数z,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是 .
17.动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a只,则20年后存活的有 只,现年20岁的这种动物活到25岁的概率是 .
18.大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2.
三.解答题(共7小题,满分48分)
19.某品牌免洗洗手液按剂型分为凝胶型、液体型,泡沫型三种型号(分别用A,B,C依次表示这三种型号).小辰和小安计划每人购买一瓶该品牌免洗洗手液,上述三种型号中的每一种免洗洗手液被选中的可能性均相同.
(1)小辰随机选择一种型号是凝胶型免洗洗手液的概率是 .
(2)请你用列表法或画树状图法,求小辰和小安选择同一种型号免洗洗手液的概率.
20.某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及8分以上为优秀),相关数据统计整理如下:
七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
七、八年级抽取学生的测试成绩统计表
年级 七年级 八年级
平均数 8 8
众数 a 7
中位数 8 b
优秀率 80% 60%
(1)填空:a= ,b= .
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可).
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
21.为了迎接建党100周年,学校举办了“感党恩 跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小颖从中随机抽取一张卡片是舞蹈社团D的概率是 ;
(2)小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.
22.为铸牢中华民族共同体意识,不断巩固民族大团结,红星中学即将举办庆祝建党100周年“中华民族一家亲,同心共筑中国梦”主题活动.学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案,为了解学生对活动方案的喜爱情况,学校随机抽取了200名学生进行调查(每人只能选择一种方案),将调结果绘制成如下两幅不完整的统计图,请你根据以下两幅图所给的信息解答下列问题.
(1)在抽取的200名学生中,选择“演讲比赛”的人数为 ,在扇形统计图中,m的值为 .
(2)根据本次调查结果,估计全校2000名学生中选择“文艺汇演”的学生大约有多少人?
(3)现从喜爱“知识竞赛”的四名同学a、b、c、d中,任选两名同学参加学校知识竞赛,请用树状图或列表法求出a同学参加的概率.
23.某校以“我最喜爱的书籍”为主题,对全校学生进行随机抽样调查,每个被调查的学生必须从“科普”、“绘画”、“诗歌”、“散文”四类书籍中选择最喜欢的一类,学校的调查结果如图:
图中信息解答下列问题
(1)本次被调查的学生有 人;
(2)根据统计图中“散文”类所对应的圆心角的度数为 ,请补充条形统计图.
(3)最喜爱“科普”类的4名学生中有1名女生,3名男生,现从4名学生中随机抽取两人参加学校举办的科普知识宣传活动,请用列表或画树状图的方法求出所选的两人恰好都是男生的概率.
24.“网红”长沙入选2021年“五一”假期热门旅游城市.本市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率;
(2)请你估计纸箱中白球的数量接近多少?
25.某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了 名学生;若该校共有1500名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
参考答案
一.选择题(共12小题,满分48分)
1.解:把“垃圾分类”“文明出行”“低碳环保”三个宣传队分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,小华和小丽恰好选到同一个宣传队的结果有3种,
∴小华和小丽恰好选到同一个宣传队的概率为=,
故选:C.
2.解:画树状图如图:
,
共有6个等可能的结果,恰好取到红色帽子和红色围巾的结果有1个,
∴恰好取到红色帽子和红色围巾的概率为,
故选:C.
3.解:根据题意画图如下:
共有4种等可能结果,其中妙妙上学时在这三个路口都直接通过的只有1种结果,
所以妙妙上学时在这两个路口都直接通过的概率为,
故选:A.
4.解:画树状图如图:
共有12种等可能的结果,恰好抽到2名女学生的结果有6种,
∴恰好抽到2名女学生的概率为=,
故选:B.
5.解:用列表法表示所有可能出现的结果情况如下:
共有20种等可能出现的结果情况,其中两球上的数字都是奇数的有6种,
所以从中随机一次摸出两个小球,小球上的数字都是奇数的概率为=,
故选:C.
6.解:将从左到右的三条竖线分别记作a、b、c,将从上到下的三条横线分别记作m、n、l,列表如下,
ab bc ac
mn ab、mn bc、mn ac、mn
nl ab、nl bc、nl ac、nl
ml ab、ml bc、ml ac、ml
由表可知共有9种等可能结果,其中所选矩形含点A的有bc、mn;bc、ml;ac、mn;ac、ml这4种结果,
∴所选矩形含点A的概率,
故选:D.
7.解:样本中身高不低于170cm的频率==0.68,
所以估计抽查该地区一名九年级男生的身高不低于170cm的概率是0.68.
故选:C.
8.解:假设不规则图案面积为xm2,
由已知得:长方形面积为20m2,
根据几何概率公式小球落在不规则图案的概率为:,
当事件A试验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上有:,解得x=7.
故选:B.
9.解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
∴袋子中红球的个数最有可能是5个,
故选:A.
10.解:设袋中有黄球x个,由题意得=0.2,
解得x=16.
故选:D.
11.解:设袋中白球有x个,根据题意,
得:,
解得x=2.
所以袋中白球有2个.
故选:A.
12.解:当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以此时“钉尖向上”的频率是:308÷500=0.616,但“钉尖向上”的概率不一定是0.616,故①错误,不符合题意,
随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618.故②正确,符合题意,
③当投掷次数是5000时,“钉尖向上”的频率不一定是0.618,正确,符合题意,
若再次用计算机模拟试验,则当投掷次数为1000时,“钉尖向上”的概率可能是0.620,但不一定是0.620,故④错误,不符合题意.
合理的有②③
故选:B.
二.填空题(共6小题,满分24分)
13.解:画树状图为:
共有6种等可能的结果,它们是:(﹣2,4),(﹣2,5),(4,﹣2),(4,5),(5,4),(5,﹣2),
其中点P在第四象限的结果数为2,即(4,﹣2),(5,﹣2),
所以点P在第四象限的概率==.
故答案为.
14.解:把开关S1,S2,S3分别记为A、B、C,
画树状图如图:
共有6种等可能的结果,能让两个小灯泡同时发光的结果有2种,
∴能让两个小灯泡同时发光的概率为=,
故答案为:.
15.解:∵一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,
∴它有6种路径,
∵获得食物的有2种路径,
∴它遇到食物的概率是:
=.
故答案为:.
16.解:该三角形的顺序旋转和与逆序旋转和的差为(4x+2z+3y)﹣(3x+2y+4z)=x+y﹣2z,
画树状图为:
共有12种等可能的结果,其中此三角形的顺序旋转和与逆序旋转和的差都小于4的结果数为9,
所以三角形的顺序旋转和与逆序旋转和的差都小于4的概率==.
故答案为.
17.解:若设刚出生的这种动物共有a只,则20年后存活的有0.8a只,
设共有这种动物x只,则活到20岁的只数为0.8x,活到25岁的只数为0.5x,
故现年20岁到这种动物活到25岁的概率为=,
故答案为:0.8a,.
18.解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴点落入黑色部分的概率为0.6,
∵边长为2cm的正方形的面积为4cm2,
设黑色部分的面积为S,
则=0.6,
解得S=2.4(cm2).
∴估计黑色部分的总面积约为2.4cm2.
故答案为:2.4.
三.解答题(共7小题,满分48分)
19.解:(1)小辰随机选择一种型号是凝胶型免洗洗手液的概率是,
故答案为:;
(2)列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由表可知,共有9种等可能结果,其中小辰和小安选择同一种型号免洗洗手液有3种结果,
所以小辰和小安选择同一种型号免洗洗手液的概率为=.
20.解:(1)由众数的定义得:a=8,
八年级抽取学生的测试成绩的中位数为8(分),
故答案为:8,8;
(2)七年级的学生党史知识掌握得较好,理由如下:
∵七年级的优秀率大于八年级的优秀率,
∴七年级的学生党史知识掌握得较好;
(3)500×80%+500×60%=700(人),
即估计七、八年级学生对党史知识掌握能够达到优秀的总人数为700人;
(4)把七年级获得10分的学生记为A,八年级获得10分的学生记为B,
画树状图如图:
共有12种等可能的结果,被选中的2人恰好是七、八年级各1人的结果有6种,
∴被选中的2人恰好是七、八年级各1人的概率为=.
21.解:(1)∵共有4种可能出现的结果,其中是舞蹈社团D的有1种,
∴小颖从中随机抽取一张卡片是舞蹈社团D的概率是,
故答案为:;
(2)用列表法表示所有可能出现的结果如下:
共有12种可能出现的结果,每种结果出现的可能性相同,其中有一张是演讲社团C的有6种,
∴小颖抽取的两张卡片中有一张是演讲社团C的概率是=.
22.解:(1)在抽取的200名学生中,选择“演讲比赛”的人数为200×20%=40(人),
则选择“书画展览”的人数为200﹣(40+80+20)=60(人),
∴在扇形统计图中,m%=×100%=30%,即m=30,
故答案为:40人,30;
(2)估计全校2000名学生中选择“文艺汇演”的学生大约有2000×=800(人);
(3)列表如下:
a b c d
a (b,a) (c,a) (d,a)
b (a,b) (c,b) (d,b)
c (a,c) (b,c) (d,c)
d (a,d) (b,d) (c,d)
由表可知,共有12种等可能结果,其中a同学参加的有6种结果,
所以a同学参加的概率为=.
23.解:(1)20÷40%=50(人),
所以本次被调查的学生有50人;
故答案为50;
(2)“散文”类所对应的圆心角的度数为360°×=72°;
最喜欢“绘画”类的人数为50﹣4﹣20﹣10=16(人),
条形统计图补充为:
故答案为72°;
(3)画树状图为:
共有12种等可能的结果,其中所选的两人恰好都是男生的结果数为6,
所以所选的两人恰好都是男生的概率==.
24.解:(1)参与该游戏可免费得到景点吉祥物的频率为=0.25;
(2)设纸箱中白球的数量为x,
则=0.25,
解得x=36,
经检验x=36是分式方程的解且符合实际,
所以估计纸箱中白球的数量接近36.
25.解:(1)爱好运动的人数为40,所占百分比为40%
∴共调查人数为:40÷40%=100,
爱好运动的学生人数所占的百分比为40%,
∴全校爱好运动的学生共有:1500×40%=600人;
故答案为:100,600;
(2)爱好上网的人数所占百分比为10%
∴爱好上网人数为:100×10%=10,
∴爱好阅读人数为:100﹣40﹣20﹣10=30,
补全条形统计图,如图所示,
阅读部分圆心角是360°×=108°,
故答案为:108;
(3)爱好阅读的学生人数所占的百分比30%,
∴用频率估计概率,则选出的恰好是爱好阅读的学生的概率为;
故答案为:.
一.选择题(共12小题,满分48分)
1.某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )
A. B. C. D.
2.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
3.妙妙上学经过两个路口,如果每个路口可直接通过和需等待的可能性相等,那么妙妙上学时在这两个路口都直接通过的概率是( )
A. B. C. D.
4.为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )
A. B. C. D.
5.在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )
A. B. C. D.
6.如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
A. B. C. D.
7.为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下:
身高x/cm x<160 160≤x<170 170≤x<180 x≥180
人数 60 260 550 130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于170cm的概率是( )A.0.32 B.0.55 C.0.68 D.0.87
8.如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2 B.7m2 C.8m2 D.9m2
9.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5 B.10 C.12 D.15
10.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球试验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个 B.4个 C.18个 D.16个
11.在一个不透明的袋子里装有若干个白球和6个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有( )
A.2个 B.4个 C.14个 D.18个
12.如图,显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.下面有四个推断:①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③当投掷次数是5000时,“钉尖向上”的频率不一定是0.618;④若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.其中合理的是( )
A.①② B.②③ C.③④ D.②④
二.填空题(共6小题,满分24分)
13.从﹣2,4,5这3个数中,任取两个数作为点P的坐标,则点P在第四象限的概率是 .
14.如图所示,电路连接完好,且各元件工作正常.随机闭合开关S1,S2,S3中的两个,能让两个小灯泡同时发光的概率是 .
15.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中一条路径,则它遇到食物的概率是 .
16.我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和.如图1,ar+cq+bp是该三角形的顺序旋转和,ap+bq+cr是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数z,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是 .
17.动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a只,则20年后存活的有 只,现年20岁的这种动物活到25岁的概率是 .
18.大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2.
三.解答题(共7小题,满分48分)
19.某品牌免洗洗手液按剂型分为凝胶型、液体型,泡沫型三种型号(分别用A,B,C依次表示这三种型号).小辰和小安计划每人购买一瓶该品牌免洗洗手液,上述三种型号中的每一种免洗洗手液被选中的可能性均相同.
(1)小辰随机选择一种型号是凝胶型免洗洗手液的概率是 .
(2)请你用列表法或画树状图法,求小辰和小安选择同一种型号免洗洗手液的概率.
20.某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及8分以上为优秀),相关数据统计整理如下:
七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
七、八年级抽取学生的测试成绩统计表
年级 七年级 八年级
平均数 8 8
众数 a 7
中位数 8 b
优秀率 80% 60%
(1)填空:a= ,b= .
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可).
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
21.为了迎接建党100周年,学校举办了“感党恩 跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小颖从中随机抽取一张卡片是舞蹈社团D的概率是 ;
(2)小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.
22.为铸牢中华民族共同体意识,不断巩固民族大团结,红星中学即将举办庆祝建党100周年“中华民族一家亲,同心共筑中国梦”主题活动.学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案,为了解学生对活动方案的喜爱情况,学校随机抽取了200名学生进行调查(每人只能选择一种方案),将调结果绘制成如下两幅不完整的统计图,请你根据以下两幅图所给的信息解答下列问题.
(1)在抽取的200名学生中,选择“演讲比赛”的人数为 ,在扇形统计图中,m的值为 .
(2)根据本次调查结果,估计全校2000名学生中选择“文艺汇演”的学生大约有多少人?
(3)现从喜爱“知识竞赛”的四名同学a、b、c、d中,任选两名同学参加学校知识竞赛,请用树状图或列表法求出a同学参加的概率.
23.某校以“我最喜爱的书籍”为主题,对全校学生进行随机抽样调查,每个被调查的学生必须从“科普”、“绘画”、“诗歌”、“散文”四类书籍中选择最喜欢的一类,学校的调查结果如图:
图中信息解答下列问题
(1)本次被调查的学生有 人;
(2)根据统计图中“散文”类所对应的圆心角的度数为 ,请补充条形统计图.
(3)最喜爱“科普”类的4名学生中有1名女生,3名男生,现从4名学生中随机抽取两人参加学校举办的科普知识宣传活动,请用列表或画树状图的方法求出所选的两人恰好都是男生的概率.
24.“网红”长沙入选2021年“五一”假期热门旅游城市.本市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率;
(2)请你估计纸箱中白球的数量接近多少?
25.某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了 名学生;若该校共有1500名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
参考答案
一.选择题(共12小题,满分48分)
1.解:把“垃圾分类”“文明出行”“低碳环保”三个宣传队分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,小华和小丽恰好选到同一个宣传队的结果有3种,
∴小华和小丽恰好选到同一个宣传队的概率为=,
故选:C.
2.解:画树状图如图:
,
共有6个等可能的结果,恰好取到红色帽子和红色围巾的结果有1个,
∴恰好取到红色帽子和红色围巾的概率为,
故选:C.
3.解:根据题意画图如下:
共有4种等可能结果,其中妙妙上学时在这三个路口都直接通过的只有1种结果,
所以妙妙上学时在这两个路口都直接通过的概率为,
故选:A.
4.解:画树状图如图:
共有12种等可能的结果,恰好抽到2名女学生的结果有6种,
∴恰好抽到2名女学生的概率为=,
故选:B.
5.解:用列表法表示所有可能出现的结果情况如下:
共有20种等可能出现的结果情况,其中两球上的数字都是奇数的有6种,
所以从中随机一次摸出两个小球,小球上的数字都是奇数的概率为=,
故选:C.
6.解:将从左到右的三条竖线分别记作a、b、c,将从上到下的三条横线分别记作m、n、l,列表如下,
ab bc ac
mn ab、mn bc、mn ac、mn
nl ab、nl bc、nl ac、nl
ml ab、ml bc、ml ac、ml
由表可知共有9种等可能结果,其中所选矩形含点A的有bc、mn;bc、ml;ac、mn;ac、ml这4种结果,
∴所选矩形含点A的概率,
故选:D.
7.解:样本中身高不低于170cm的频率==0.68,
所以估计抽查该地区一名九年级男生的身高不低于170cm的概率是0.68.
故选:C.
8.解:假设不规则图案面积为xm2,
由已知得:长方形面积为20m2,
根据几何概率公式小球落在不规则图案的概率为:,
当事件A试验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上有:,解得x=7.
故选:B.
9.解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
∴袋子中红球的个数最有可能是5个,
故选:A.
10.解:设袋中有黄球x个,由题意得=0.2,
解得x=16.
故选:D.
11.解:设袋中白球有x个,根据题意,
得:,
解得x=2.
所以袋中白球有2个.
故选:A.
12.解:当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以此时“钉尖向上”的频率是:308÷500=0.616,但“钉尖向上”的概率不一定是0.616,故①错误,不符合题意,
随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618.故②正确,符合题意,
③当投掷次数是5000时,“钉尖向上”的频率不一定是0.618,正确,符合题意,
若再次用计算机模拟试验,则当投掷次数为1000时,“钉尖向上”的概率可能是0.620,但不一定是0.620,故④错误,不符合题意.
合理的有②③
故选:B.
二.填空题(共6小题,满分24分)
13.解:画树状图为:
共有6种等可能的结果,它们是:(﹣2,4),(﹣2,5),(4,﹣2),(4,5),(5,4),(5,﹣2),
其中点P在第四象限的结果数为2,即(4,﹣2),(5,﹣2),
所以点P在第四象限的概率==.
故答案为.
14.解:把开关S1,S2,S3分别记为A、B、C,
画树状图如图:
共有6种等可能的结果,能让两个小灯泡同时发光的结果有2种,
∴能让两个小灯泡同时发光的概率为=,
故答案为:.
15.解:∵一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,
∴它有6种路径,
∵获得食物的有2种路径,
∴它遇到食物的概率是:
=.
故答案为:.
16.解:该三角形的顺序旋转和与逆序旋转和的差为(4x+2z+3y)﹣(3x+2y+4z)=x+y﹣2z,
画树状图为:
共有12种等可能的结果,其中此三角形的顺序旋转和与逆序旋转和的差都小于4的结果数为9,
所以三角形的顺序旋转和与逆序旋转和的差都小于4的概率==.
故答案为.
17.解:若设刚出生的这种动物共有a只,则20年后存活的有0.8a只,
设共有这种动物x只,则活到20岁的只数为0.8x,活到25岁的只数为0.5x,
故现年20岁到这种动物活到25岁的概率为=,
故答案为:0.8a,.
18.解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴点落入黑色部分的概率为0.6,
∵边长为2cm的正方形的面积为4cm2,
设黑色部分的面积为S,
则=0.6,
解得S=2.4(cm2).
∴估计黑色部分的总面积约为2.4cm2.
故答案为:2.4.
三.解答题(共7小题,满分48分)
19.解:(1)小辰随机选择一种型号是凝胶型免洗洗手液的概率是,
故答案为:;
(2)列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由表可知,共有9种等可能结果,其中小辰和小安选择同一种型号免洗洗手液有3种结果,
所以小辰和小安选择同一种型号免洗洗手液的概率为=.
20.解:(1)由众数的定义得:a=8,
八年级抽取学生的测试成绩的中位数为8(分),
故答案为:8,8;
(2)七年级的学生党史知识掌握得较好,理由如下:
∵七年级的优秀率大于八年级的优秀率,
∴七年级的学生党史知识掌握得较好;
(3)500×80%+500×60%=700(人),
即估计七、八年级学生对党史知识掌握能够达到优秀的总人数为700人;
(4)把七年级获得10分的学生记为A,八年级获得10分的学生记为B,
画树状图如图:
共有12种等可能的结果,被选中的2人恰好是七、八年级各1人的结果有6种,
∴被选中的2人恰好是七、八年级各1人的概率为=.
21.解:(1)∵共有4种可能出现的结果,其中是舞蹈社团D的有1种,
∴小颖从中随机抽取一张卡片是舞蹈社团D的概率是,
故答案为:;
(2)用列表法表示所有可能出现的结果如下:
共有12种可能出现的结果,每种结果出现的可能性相同,其中有一张是演讲社团C的有6种,
∴小颖抽取的两张卡片中有一张是演讲社团C的概率是=.
22.解:(1)在抽取的200名学生中,选择“演讲比赛”的人数为200×20%=40(人),
则选择“书画展览”的人数为200﹣(40+80+20)=60(人),
∴在扇形统计图中,m%=×100%=30%,即m=30,
故答案为:40人,30;
(2)估计全校2000名学生中选择“文艺汇演”的学生大约有2000×=800(人);
(3)列表如下:
a b c d
a (b,a) (c,a) (d,a)
b (a,b) (c,b) (d,b)
c (a,c) (b,c) (d,c)
d (a,d) (b,d) (c,d)
由表可知,共有12种等可能结果,其中a同学参加的有6种结果,
所以a同学参加的概率为=.
23.解:(1)20÷40%=50(人),
所以本次被调查的学生有50人;
故答案为50;
(2)“散文”类所对应的圆心角的度数为360°×=72°;
最喜欢“绘画”类的人数为50﹣4﹣20﹣10=16(人),
条形统计图补充为:
故答案为72°;
(3)画树状图为:
共有12种等可能的结果,其中所选的两人恰好都是男生的结果数为6,
所以所选的两人恰好都是男生的概率==.
24.解:(1)参与该游戏可免费得到景点吉祥物的频率为=0.25;
(2)设纸箱中白球的数量为x,
则=0.25,
解得x=36,
经检验x=36是分式方程的解且符合实际,
所以估计纸箱中白球的数量接近36.
25.解:(1)爱好运动的人数为40,所占百分比为40%
∴共调查人数为:40÷40%=100,
爱好运动的学生人数所占的百分比为40%,
∴全校爱好运动的学生共有:1500×40%=600人;
故答案为:100,600;
(2)爱好上网的人数所占百分比为10%
∴爱好上网人数为:100×10%=10,
∴爱好阅读人数为:100﹣40﹣20﹣10=30,
补全条形统计图,如图所示,
阅读部分圆心角是360°×=108°,
故答案为:108;
(3)爱好阅读的学生人数所占的百分比30%,
∴用频率估计概率,则选出的恰好是爱好阅读的学生的概率为;
故答案为:.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
