31.1锐角三角函数

(共18张PPT)
31.1锐角三角函数
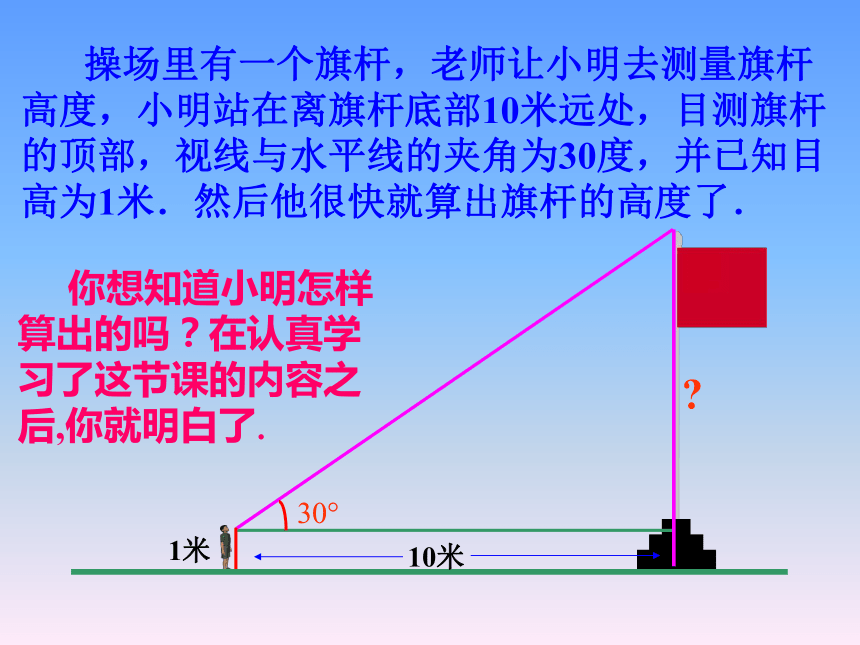
操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为30度，并已知目高为1米．然后他很快就算出旗杆的高度了．
1米
10米

你想知道小明怎样算出的吗？在认真学习了这节课的内容之后,你就明白了.
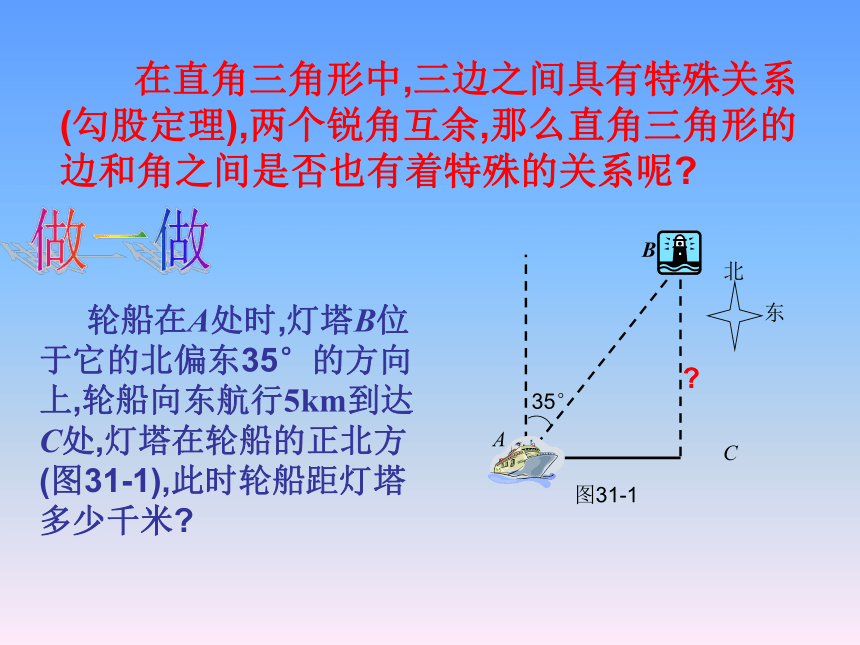
在直角三角形中,三边之间具有特殊关系(勾股定理),两个锐角互余,那么直角三角形的边和角之间是否也有着特殊的关系呢
轮船在A处时,灯塔B位于它的北偏东35°的方向上,轮船向东航行5km到达C处,灯塔在轮船的正北方(图31-1),此时轮船距灯塔多少千米
A
B
C
35°
北
东
图31-1

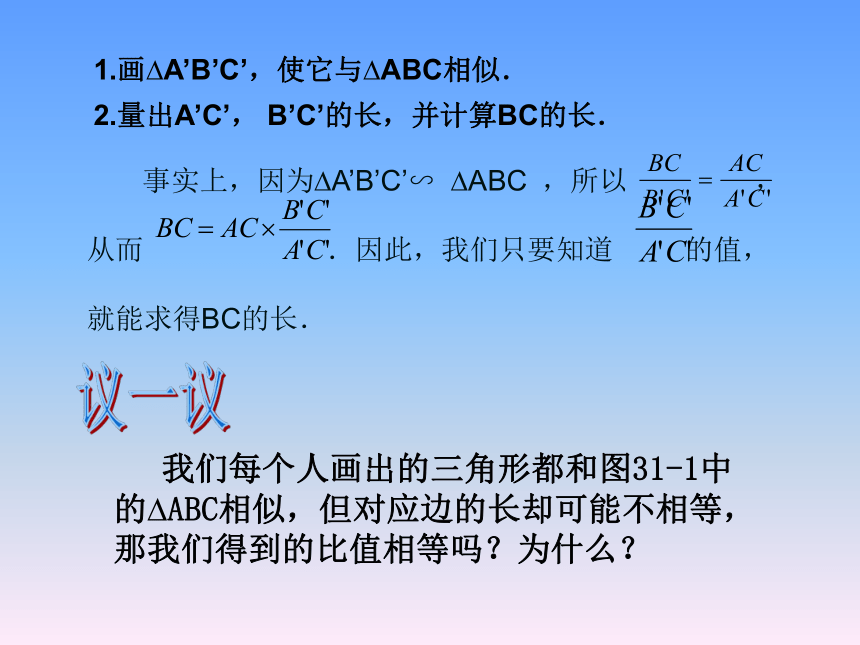
1.画 A’B’C’，使它与 ABC相似．
2.量出A’C’， B’C’的长，并计算BC的长．
事实上，因为 A’B’C’∽ ABC ，所以 ，
从而 ．因此，我们只要知道 的值，
就能求得BC的长．
我们每个人画出的三角形都和图31-1中的 ABC相似，但对应边的长却可能不相等，那我们得到的比值相等吗？为什么？
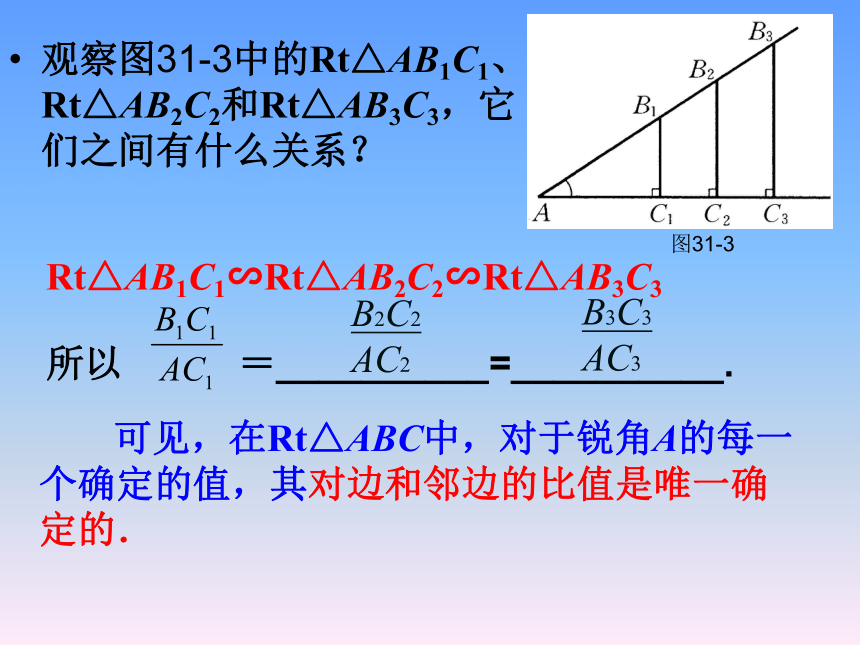
观察图31-3中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3，它们之间有什么关系？
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以　　　＝__________=__________.
可见，在Rt△ABC中，对于锐角A的每一个确定的值，其对边和邻边的比值是唯一确定的．
B2C2
AC2
B3C3
AC3
图31-3
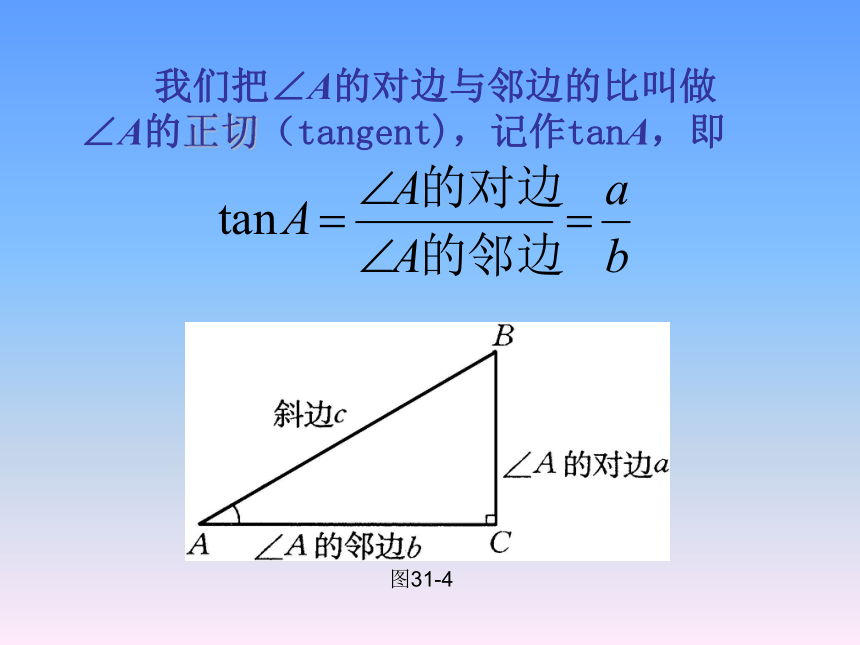
我们把∠A的对边与邻边的比叫做∠A的正切（tangent)，记作tanA，即
图31-4
　　a
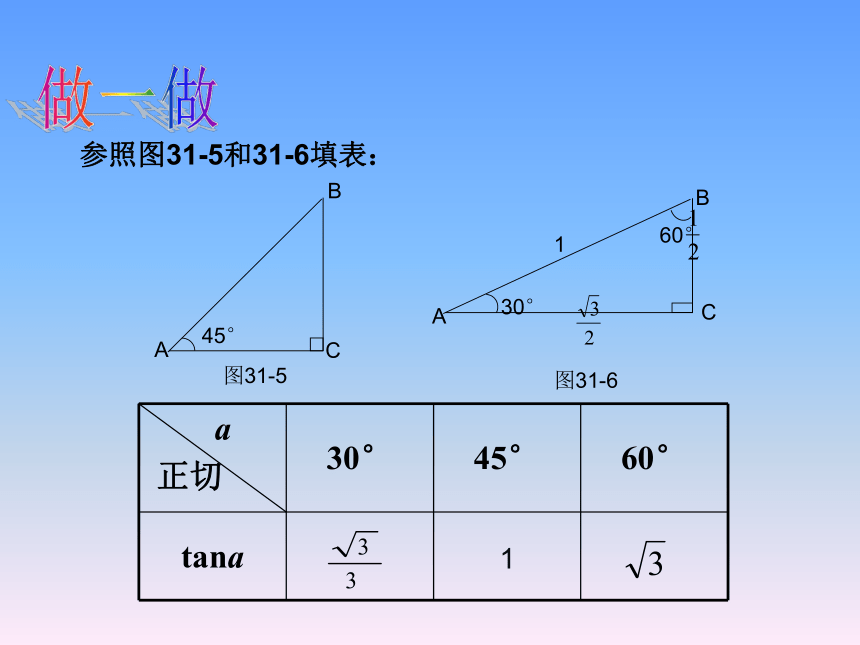
正切 30° 45° 60°
tana
图31-6
参照图31-5和31-6填表：
45°
A
B
C
图31-5
30°
A
B
C
60°
1
1
操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为30度，并已知目高为1米．然后他很快就算出旗杆的高度了．
1米
10米

h=10×tan30o+1=
想一想
对于锐角A的每一个确定的值，其对边与斜边、邻边与斜边的比值也是唯一确定的吗？
图31-4
这两个比值也都是唯一确定的，记作sin A和cos A，即
sin A=
cos A=
分别叫做∠A的正弦和余弦，锐角∠A的正弦、余弦和正切都叫做锐角∠A的三角函数．
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、 sinA 是一个比值 4、sinA 没有单位
理解定义：
1、你认为∠A的正弦、余弦的定义有什么
区别？
2、你能利用直角三角形的三边关系得到
sinA与 cosA的取值范围吗？
0＜sin A＜1，0＜cos A＜1
练习
1、求出下图所示的Rt△ABC中∠A的三个三角函数值．
15
8
sinA=
cosA=
tanA=
2、右图中∠ACB=90° ，CD⊥AB，指出∠A的对边、邻边，如果CD=5，AC=10，则sin∠ACD=？ sin ∠DCB= ？
A
B
C
D
3、填表：
a三角函数 30o 45o 60o
sina
cosa
tana
例1 求下列各式的值：
（1）2sin30°+ 3tan30°— tan45°
（2）sin245°+ tan60°sin60°
解：（1）
（2）
（1）在△ABC中，∠B=90 ，BC=3，AC=4，则tanA= cosA=
小结
通过我们这一节课的探索与学习，你一定有好多的收获，你能把这些知识点加以收集与总结吗？
作业
1、课本P113—习题1～4．
2、阅读P114页“读一读”．
3、预习下一节内容．
4、准备一个科学计算器．