3.5 专题复习:受力分析 共点力的平衡课后作业— 2021-2022学年高一上学期物理人教版(2019)必修第一册(Word含答案)
文档属性
| 名称 | 3.5 专题复习:受力分析 共点力的平衡课后作业— 2021-2022学年高一上学期物理人教版(2019)必修第一册(Word含答案) | 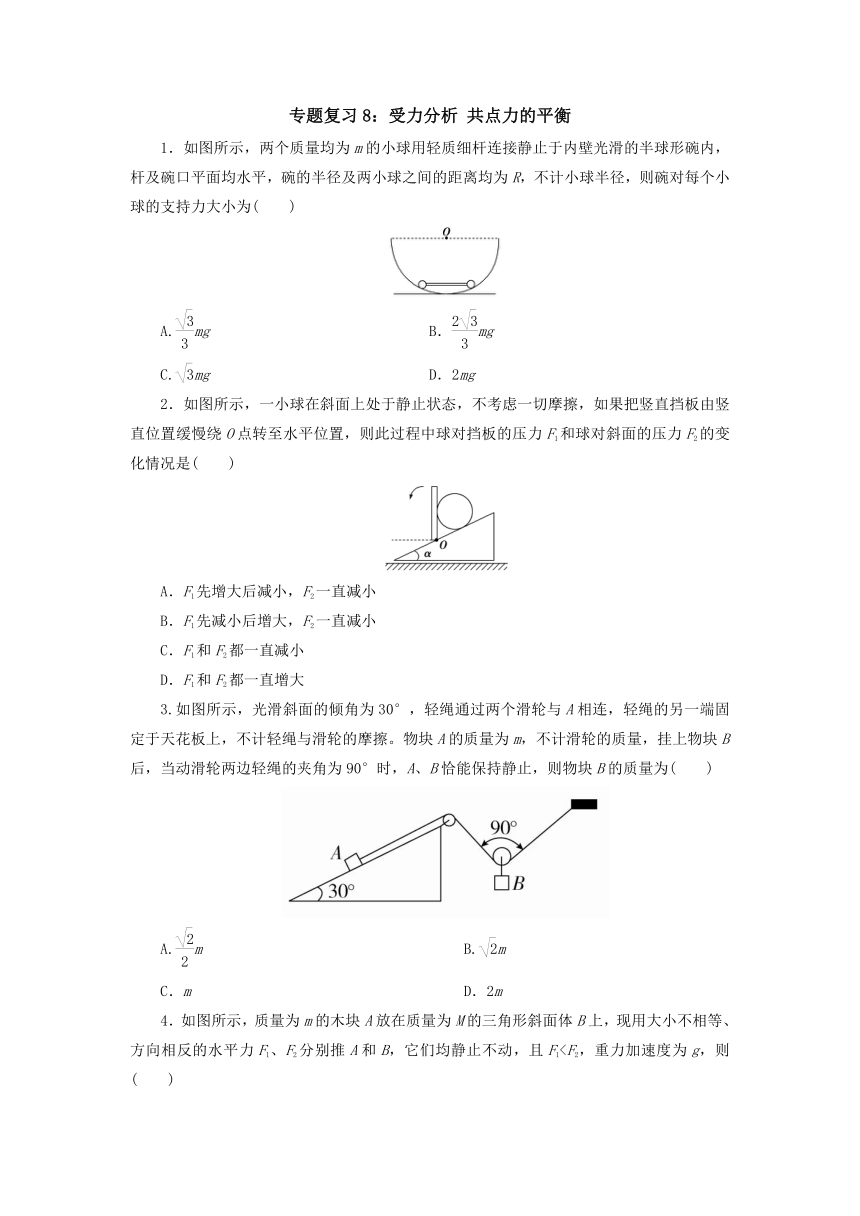 | |
| 格式 | docx | ||
| 文件大小 | 197.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-12 10:38:59 | ||
图片预览


文档简介
专题复习8:受力分析 共点力的平衡
1.如图所示,两个质量均为m的小球用轻质细杆连接静止于内壁光滑的半球形碗内,杆及碗口平面均水平,碗的半径及两小球之间的距离均为R,不计小球半径,则碗对每个小球的支持力大小为( )
A.mg B.mg
C.mg D.2mg
2.如图所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对挡板的压力F1和球对斜面的压力F2的变化情况是( )
A.F1先增大后减小,F2一直减小
B.F1先减小后增大,F2一直减小
C.F1和F2都一直减小
D.F1和F2都一直增大
3.如图所示,光滑斜面的倾角为30°,轻绳通过两个滑轮与A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦。物块A的质量为m,不计滑轮的质量,挂上物块B后,当动滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,则物块B的质量为( )
A.m B.m
C.m D.2m
4.如图所示,质量为m的木块A放在质量为M的三角形斜面体B上,现用大小不相等、方向相反的水平力F1、F2分别推A和B,它们均静止不动,且F1A.A受到四个力的作用
B.B对A的摩擦力方向一定沿斜面向下
C.地面对B的摩擦力方向水平向右,大小为F2-F1
D.地面对B的支持力大小一定等于(M+m)g
5.如图所示,一条细绳跨过光滑的定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计滑轮的质量,当两球平衡时OA绳与水平方向的夹角为2θ,OB绳与水平方向的夹角为θ,球B的质量为m,则( )
A.A球的质量为
B.A球的质量可能小于B球的质量
C.滑轮轴受到的作用力大小为
D.细绳的张力大小为
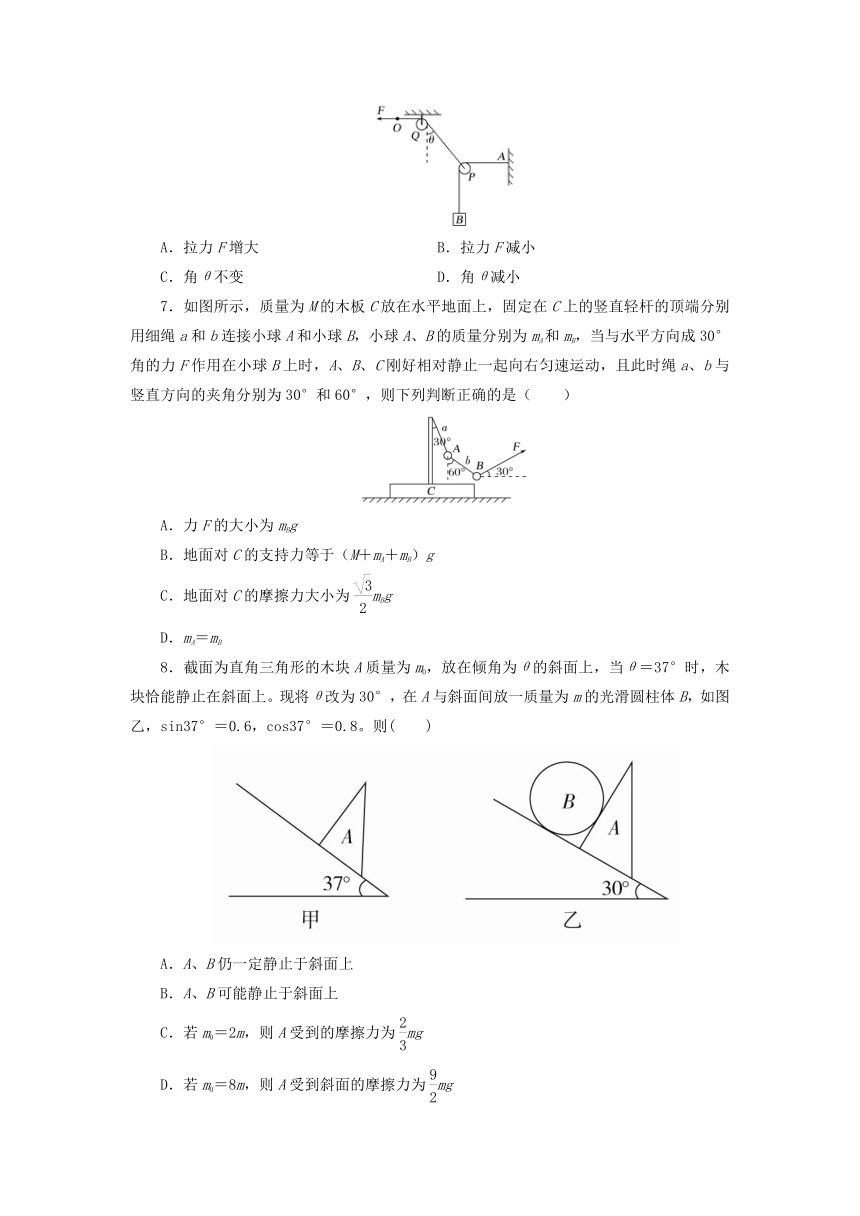
6.如图所示,一根绳子一端固定于竖直墙上的A点,另一端绕过动滑轮P悬挂一重物B,其中绳子的PA段处于水平状态,另一根绳子一端与动滑轮P的轴相连,在绕过光滑的定滑轮Q后在其端点O施加一水平向左的外力F,使整个系统处于平衡状态,滑轮均为光滑、轻质,且均可看作质点,现拉动绳子的端点O使其向左缓慢移动一小段距离后达到新的平衡状态,则该平衡状态与原平衡状态相比较( )
A.拉力F增大 B.拉力F减小
C.角θ不变 D.角θ减小
7.如图所示,质量为M的木板C放在水平地面上,固定在C上的竖直轻杆的顶端分别用细绳a和b连接小球A和小球B,小球A、B的质量分别为mA和mB,当与水平方向成30°角的力F作用在小球B上时,A、B、C刚好相对静止一起向右匀速运动,且此时绳a、b与竖直方向的夹角分别为30°和60°,则下列判断正确的是( )
A.力F的大小为mBg
B.地面对C的支持力等于(M+mA+mB)g
C.地面对C的摩擦力大小为mBg
D.mA=mB
8.截面为直角三角形的木块A质量为m0,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上。现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,sin37°=0.6,cos37°=0.8。则( )
A.A、B仍一定静止于斜面上
B.A、B可能静止于斜面上
C.若m0=2m,则A受到的摩擦力为mg
D.若m0=8m,则A受到斜面的摩擦力为mg
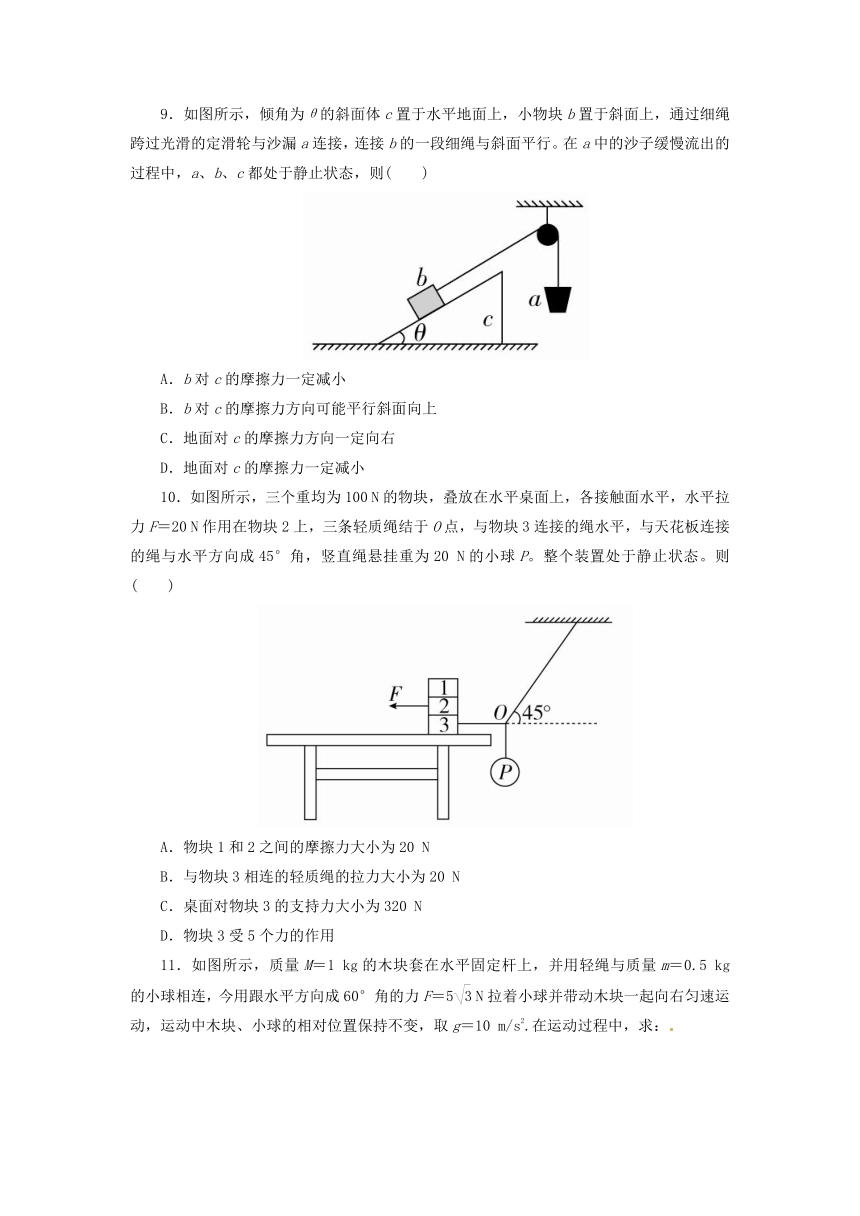
9.如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏a连接,连接b的一段细绳与斜面平行。在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )
A.b对c的摩擦力一定减小
B.b对c的摩擦力方向可能平行斜面向上
C.地面对c的摩擦力方向一定向右
D.地面对c的摩擦力一定减小
10.如图所示,三个重均为100 N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20 N作用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45°角,竖直绳悬挂重为20 N的小球P。整个装置处于静止状态。则( )
A.物块1和2之间的摩擦力大小为20 N
B.与物块3相连的轻质绳的拉力大小为20 N
C.桌面对物块3的支持力大小为320 N
D.物块3受5个力的作用
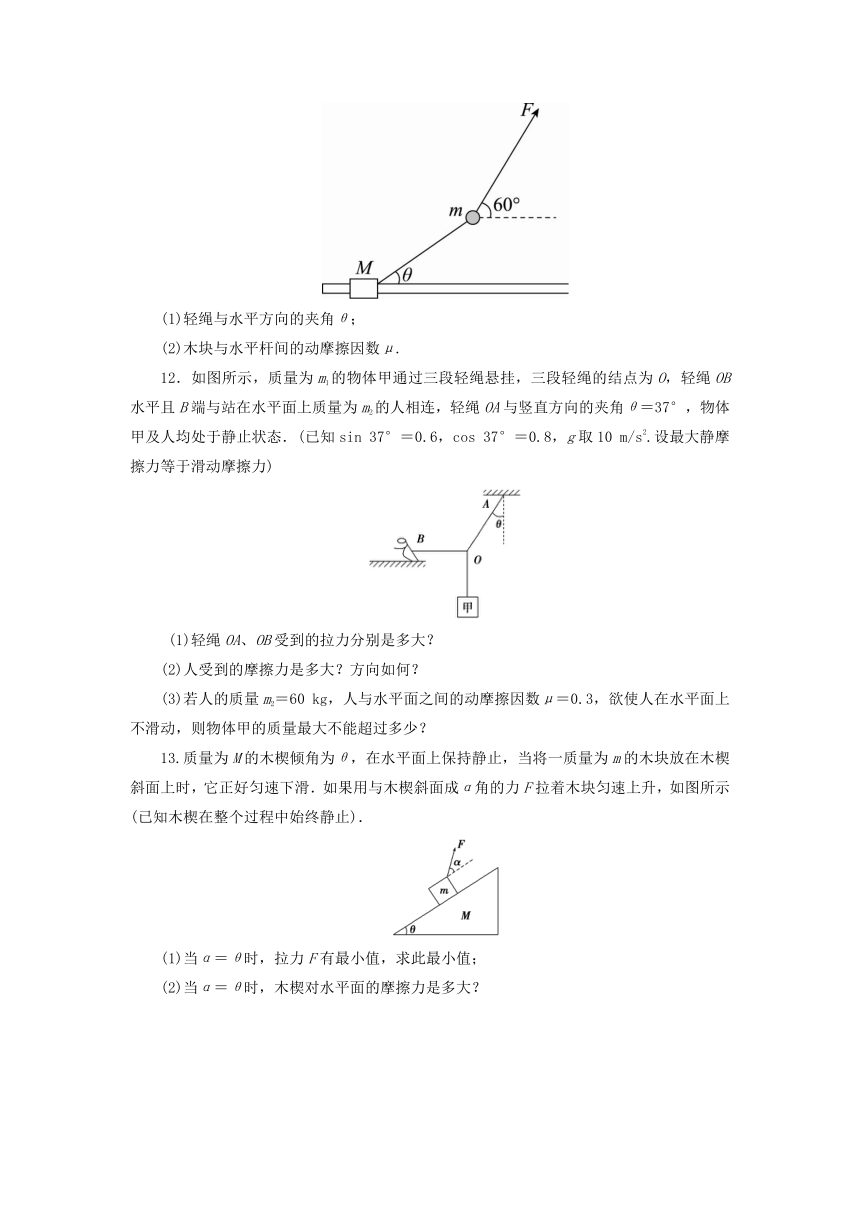
11.如图所示,质量M=1 kg的木块套在水平固定杆上,并用轻绳与质量m=0.5 kg的小球相连,今用跟水平方向成60°角的力F=5 N拉着小球并带动木块一起向右匀速运动,运动中木块、小球的相对位置保持不变,取g=10 m/s2.在运动过程中,求:
(1)轻绳与水平方向的夹角θ;
(2)木块与水平杆间的动摩擦因数μ.
12.如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上质量为m2的人相连,轻绳OA与竖直方向的夹角θ=37°,物体甲及人均处于静止状态.(已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2.设最大静摩擦力等于滑动摩擦力)
(1)轻绳OA、OB受到的拉力分别是多大?
(2)人受到的摩擦力是多大?方向如何?
(3)若人的质量m2=60 kg,人与水平面之间的动摩擦因数μ=0.3,欲使人在水平面上不滑动,则物体甲的质量最大不能超过多少?
13.质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在木楔斜面上时,它正好匀速下滑.如果用与木楔斜面成α角的力F拉着木块匀速上升,如图所示(已知木楔在整个过程中始终静止).
(1)当α=θ时,拉力F有最小值,求此最小值;
(2)当α=θ时,木楔对水平面的摩擦力是多大?
参考答案
1.解析 以其中一小球为研究对象,受力情况如图所示.根据题意可知θ=30°,根据平衡条件可知:N1==mg,选项B正确.
2.解析 挡板缓慢转动小球处于动态平衡状态,在转动过程中,球受重力、斜面的支持力、挡板的弹力组成矢量三角形的变化情况如图所示,由图可知此过程中斜面对小球的支持力不断减小,挡板对小球的弹力先减小后增大,再由牛顿第三定律知B对.
3.解析 先以A为研究对象,由A物块受力及平衡条件可得,绳中张力FT=mgsin30°。再以动滑轮为研究对象,分析其受力并由平衡条件有mBg=FT,解得mB=m,A正确。
4.解析 以A为研究对象进行受力分析,如图所示。沿斜面方向,F1的分力和重力的分力大小关系不确定,所以B和A之间有无摩擦也不确定,故A、B错误;以整体为研究对象,水平方向:Ff=F2-F1,方向向右,竖直方向:FN=(M+m)g,故C、D正确。
5.解析 分别对A、B两球分析,运用合成法,如图:
由几何知识得:FTsin 2θ=mAg FTsin θ=mBg 故mA∶mB=sin 2θ∶sin θ=2cos θ∶1;mA>mB.故A、B错误;绳子上的张力FT==,滑轮轴受到的作用力大小为:F=2FTcos=,故C正确,D错误.
6.解析 以动滑轮P为研究对象,AP、BP段绳子受的力始终等于B的重力,两绳子拉力的合力在∠APB的角平分线上,拉动绳子后,滑轮向上运动,两绳子夹角减小,两拉力的合力增大,故F增大,A项正确,B项错;PQ与竖直方向夹角等于∠APB的一半,故拉动绳子后角θ减小,C项错,D项正确。
7.解析 对小球B受力分析,水平方向有Fcos 30°=Tbcos 30°,得Tb=F,竖直方向有Fsin 30°+Tbsin 30°=mBg,解得F=mBg,故A正确;对小球A受力分析,竖直方向有mAg+Tbsin 30°=Tasin 60°,水平方向有Tasin 30°=Tbsin 60°,联立解得mA=mB,故D正确;以A、B、C整体为研究对象受力分析,竖直方向有FN+Fsin 30°=(M+mA+mB)g,可见FN小于(M+mA+mB)g,故B错误;水平方向有Ff=Fcos 30°=mBgcos 30°=mBg,故C正确。
8.解析 由题意可知,当θ=37°时,木块恰能静止在斜面上,则有μm0gcos37°=m0gsin37°,代入数据解得μ=0.75。现将θ改为30°,0.75>tan30°,木块A相对斜面不滑动,因此木块A、圆柱体B是否静止在斜面上,由圆柱体B对木块A弹力决定,木块A、圆柱体B可能静止于斜面上,故A错误,B正确;若m0=2m,则mgsin30°+m0gsin30°=mg,而Ff=μFN=0.75×m0gcos30°=mg,因Ffmgsin30°+m0gsin30°,木块A不滑动,木块A受到斜面的静摩擦力,大小为Ff″=mgsin30°+m0gsin30°=mg,故D正确。
9.解析 设a、b的重力分别为Ga、Gb,a保持静止,故a对细线的拉力等于a的重力。对b受力分析可知,若Ga=Gbsinθ,b受到c的摩擦力为零,a的重力减小,则b受到c的摩擦力沿斜面向上且增大;若GaGbsinθ,b受到c的摩擦力沿斜面向下,根据平衡条件得,Ff2=mbgsinθ+Ga,a的重力减小,则b、c间的摩擦力可能一直减小,也可能先减小到零后反向增大,A错误,B正确;以b、c整体为研究对象,由平衡条件知,地面对c的摩擦力Ff3=Gacosθ,方向水平向左,C错误;在a中的沙子缓慢流出的过程中,则摩擦力减小,D正确。
10.解析 以结点O为研究对象,受力分析如图所示,由平衡条件可求出与物块3相连的轻质绳的拉力大小为F1=GP=20 N,再以物块1、2、3为研究对象,由平衡条件可知,物块3与桌面之间的摩擦力为零,所以物块3受5个力的作用,且桌面对物块3的支持力FN=300 N,故B、D正确,C错误;以物块1为研究对象,由平衡条件可知Ff=0,A错误。
11.答案 (1)30° (2)
解析 (1)小球处于平衡状态,其所受合力为零.以小球为研究对象分析受力如图甲所示,由平衡条件得,水平方向Fcos 60°-Tcos θ=0,竖直方向Fsin 60°-Tsin θ-mg=0,解得θ=30°.
(2)以木块和小球整体为研究对象,受力分析如图乙所示,由平衡条件得,水平方向有Fcos 60°-μN=0,竖直方向有Fsin 60°+N-mg-Mg=0,解得μ=.
12.答案 (1)m1g m1g (2)m1g 方向水平向左 (3)24 kg
解析 (1)以结点O为研究对象进行受力分析,如图甲所示,
甲
由平衡条件有
FOB=FOAsin θ
FOAcos θ=m1g
联立解得FOA==m1g,
FOB=m1gtan θ=m1g
故轻绳OA、OB受到的拉力分别为m1g、m1g.
(2)对人受力分析,如图乙所示,
乙
人在水平方向受到OB绳的拉力F′OB和水平向左的静摩擦力作用,由平衡条件得Ff=F′OB
又F′OB=FOB
所以Ff=FOB=m1g.
(3)当人刚要滑动时,甲的质量达到最大,此时人受到的静摩擦力达到最大值,有Ffm=μm2g
由平衡条件得F′OBm=Ffm
又F′OBm=FOBm=m1mgtan θ=m1mg
联立解得m1m===24 kg
即物体甲的质量最大不能超过24 kg.
13.答案(1)mgsin 2θ (2)mgsin 4θ
解析 木块在木楔斜面上匀速向下运动时,有
mgsin θ=μmgcos θ,
即μ=tan θ.
(1)木块在力F作用下沿斜面向上匀速运动,有
Fcos α=mgsin θ+Ff
Fsin α+FN=mgcos θ
Ff=μFN
解得F==
=
则当α=θ时,F有最小值,为Fmin=mgsin 2θ.
(2)因为木块及木楔均处于平衡状态,整体受到地面的摩擦力等于F的水平分力,即
Ff=Fcos(α+θ)
当α=θ时,F取最小值mgsin 2θ,
Ffm=Fmincos 2θ=mg·sin 2θcos 2θ=mgsin 4θ.
1.如图所示,两个质量均为m的小球用轻质细杆连接静止于内壁光滑的半球形碗内,杆及碗口平面均水平,碗的半径及两小球之间的距离均为R,不计小球半径,则碗对每个小球的支持力大小为( )
A.mg B.mg
C.mg D.2mg
2.如图所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对挡板的压力F1和球对斜面的压力F2的变化情况是( )
A.F1先增大后减小,F2一直减小
B.F1先减小后增大,F2一直减小
C.F1和F2都一直减小
D.F1和F2都一直增大
3.如图所示,光滑斜面的倾角为30°,轻绳通过两个滑轮与A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦。物块A的质量为m,不计滑轮的质量,挂上物块B后,当动滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,则物块B的质量为( )
A.m B.m
C.m D.2m
4.如图所示,质量为m的木块A放在质量为M的三角形斜面体B上,现用大小不相等、方向相反的水平力F1、F2分别推A和B,它们均静止不动,且F1
B.B对A的摩擦力方向一定沿斜面向下
C.地面对B的摩擦力方向水平向右,大小为F2-F1
D.地面对B的支持力大小一定等于(M+m)g
5.如图所示,一条细绳跨过光滑的定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计滑轮的质量,当两球平衡时OA绳与水平方向的夹角为2θ,OB绳与水平方向的夹角为θ,球B的质量为m,则( )
A.A球的质量为
B.A球的质量可能小于B球的质量
C.滑轮轴受到的作用力大小为
D.细绳的张力大小为
6.如图所示,一根绳子一端固定于竖直墙上的A点,另一端绕过动滑轮P悬挂一重物B,其中绳子的PA段处于水平状态,另一根绳子一端与动滑轮P的轴相连,在绕过光滑的定滑轮Q后在其端点O施加一水平向左的外力F,使整个系统处于平衡状态,滑轮均为光滑、轻质,且均可看作质点,现拉动绳子的端点O使其向左缓慢移动一小段距离后达到新的平衡状态,则该平衡状态与原平衡状态相比较( )
A.拉力F增大 B.拉力F减小
C.角θ不变 D.角θ减小
7.如图所示,质量为M的木板C放在水平地面上,固定在C上的竖直轻杆的顶端分别用细绳a和b连接小球A和小球B,小球A、B的质量分别为mA和mB,当与水平方向成30°角的力F作用在小球B上时,A、B、C刚好相对静止一起向右匀速运动,且此时绳a、b与竖直方向的夹角分别为30°和60°,则下列判断正确的是( )
A.力F的大小为mBg
B.地面对C的支持力等于(M+mA+mB)g
C.地面对C的摩擦力大小为mBg
D.mA=mB
8.截面为直角三角形的木块A质量为m0,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上。现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,sin37°=0.6,cos37°=0.8。则( )
A.A、B仍一定静止于斜面上
B.A、B可能静止于斜面上
C.若m0=2m,则A受到的摩擦力为mg
D.若m0=8m,则A受到斜面的摩擦力为mg
9.如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏a连接,连接b的一段细绳与斜面平行。在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )
A.b对c的摩擦力一定减小
B.b对c的摩擦力方向可能平行斜面向上
C.地面对c的摩擦力方向一定向右
D.地面对c的摩擦力一定减小
10.如图所示,三个重均为100 N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20 N作用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45°角,竖直绳悬挂重为20 N的小球P。整个装置处于静止状态。则( )
A.物块1和2之间的摩擦力大小为20 N
B.与物块3相连的轻质绳的拉力大小为20 N
C.桌面对物块3的支持力大小为320 N
D.物块3受5个力的作用
11.如图所示,质量M=1 kg的木块套在水平固定杆上,并用轻绳与质量m=0.5 kg的小球相连,今用跟水平方向成60°角的力F=5 N拉着小球并带动木块一起向右匀速运动,运动中木块、小球的相对位置保持不变,取g=10 m/s2.在运动过程中,求:
(1)轻绳与水平方向的夹角θ;
(2)木块与水平杆间的动摩擦因数μ.
12.如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上质量为m2的人相连,轻绳OA与竖直方向的夹角θ=37°,物体甲及人均处于静止状态.(已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2.设最大静摩擦力等于滑动摩擦力)
(1)轻绳OA、OB受到的拉力分别是多大?
(2)人受到的摩擦力是多大?方向如何?
(3)若人的质量m2=60 kg,人与水平面之间的动摩擦因数μ=0.3,欲使人在水平面上不滑动,则物体甲的质量最大不能超过多少?
13.质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在木楔斜面上时,它正好匀速下滑.如果用与木楔斜面成α角的力F拉着木块匀速上升,如图所示(已知木楔在整个过程中始终静止).
(1)当α=θ时,拉力F有最小值,求此最小值;
(2)当α=θ时,木楔对水平面的摩擦力是多大?
参考答案
1.解析 以其中一小球为研究对象,受力情况如图所示.根据题意可知θ=30°,根据平衡条件可知:N1==mg,选项B正确.
2.解析 挡板缓慢转动小球处于动态平衡状态,在转动过程中,球受重力、斜面的支持力、挡板的弹力组成矢量三角形的变化情况如图所示,由图可知此过程中斜面对小球的支持力不断减小,挡板对小球的弹力先减小后增大,再由牛顿第三定律知B对.
3.解析 先以A为研究对象,由A物块受力及平衡条件可得,绳中张力FT=mgsin30°。再以动滑轮为研究对象,分析其受力并由平衡条件有mBg=FT,解得mB=m,A正确。
4.解析 以A为研究对象进行受力分析,如图所示。沿斜面方向,F1的分力和重力的分力大小关系不确定,所以B和A之间有无摩擦也不确定,故A、B错误;以整体为研究对象,水平方向:Ff=F2-F1,方向向右,竖直方向:FN=(M+m)g,故C、D正确。
5.解析 分别对A、B两球分析,运用合成法,如图:
由几何知识得:FTsin 2θ=mAg FTsin θ=mBg 故mA∶mB=sin 2θ∶sin θ=2cos θ∶1;mA>mB.故A、B错误;绳子上的张力FT==,滑轮轴受到的作用力大小为:F=2FTcos=,故C正确,D错误.
6.解析 以动滑轮P为研究对象,AP、BP段绳子受的力始终等于B的重力,两绳子拉力的合力在∠APB的角平分线上,拉动绳子后,滑轮向上运动,两绳子夹角减小,两拉力的合力增大,故F增大,A项正确,B项错;PQ与竖直方向夹角等于∠APB的一半,故拉动绳子后角θ减小,C项错,D项正确。
7.解析 对小球B受力分析,水平方向有Fcos 30°=Tbcos 30°,得Tb=F,竖直方向有Fsin 30°+Tbsin 30°=mBg,解得F=mBg,故A正确;对小球A受力分析,竖直方向有mAg+Tbsin 30°=Tasin 60°,水平方向有Tasin 30°=Tbsin 60°,联立解得mA=mB,故D正确;以A、B、C整体为研究对象受力分析,竖直方向有FN+Fsin 30°=(M+mA+mB)g,可见FN小于(M+mA+mB)g,故B错误;水平方向有Ff=Fcos 30°=mBgcos 30°=mBg,故C正确。
8.解析 由题意可知,当θ=37°时,木块恰能静止在斜面上,则有μm0gcos37°=m0gsin37°,代入数据解得μ=0.75。现将θ改为30°,0.75>tan30°,木块A相对斜面不滑动,因此木块A、圆柱体B是否静止在斜面上,由圆柱体B对木块A弹力决定,木块A、圆柱体B可能静止于斜面上,故A错误,B正确;若m0=2m,则mgsin30°+m0gsin30°=mg,而Ff=μFN=0.75×m0gcos30°=mg,因Ff
9.解析 设a、b的重力分别为Ga、Gb,a保持静止,故a对细线的拉力等于a的重力。对b受力分析可知,若Ga=Gbsinθ,b受到c的摩擦力为零,a的重力减小,则b受到c的摩擦力沿斜面向上且增大;若Ga
10.解析 以结点O为研究对象,受力分析如图所示,由平衡条件可求出与物块3相连的轻质绳的拉力大小为F1=GP=20 N,再以物块1、2、3为研究对象,由平衡条件可知,物块3与桌面之间的摩擦力为零,所以物块3受5个力的作用,且桌面对物块3的支持力FN=300 N,故B、D正确,C错误;以物块1为研究对象,由平衡条件可知Ff=0,A错误。
11.答案 (1)30° (2)
解析 (1)小球处于平衡状态,其所受合力为零.以小球为研究对象分析受力如图甲所示,由平衡条件得,水平方向Fcos 60°-Tcos θ=0,竖直方向Fsin 60°-Tsin θ-mg=0,解得θ=30°.
(2)以木块和小球整体为研究对象,受力分析如图乙所示,由平衡条件得,水平方向有Fcos 60°-μN=0,竖直方向有Fsin 60°+N-mg-Mg=0,解得μ=.
12.答案 (1)m1g m1g (2)m1g 方向水平向左 (3)24 kg
解析 (1)以结点O为研究对象进行受力分析,如图甲所示,
甲
由平衡条件有
FOB=FOAsin θ
FOAcos θ=m1g
联立解得FOA==m1g,
FOB=m1gtan θ=m1g
故轻绳OA、OB受到的拉力分别为m1g、m1g.
(2)对人受力分析,如图乙所示,
乙
人在水平方向受到OB绳的拉力F′OB和水平向左的静摩擦力作用,由平衡条件得Ff=F′OB
又F′OB=FOB
所以Ff=FOB=m1g.
(3)当人刚要滑动时,甲的质量达到最大,此时人受到的静摩擦力达到最大值,有Ffm=μm2g
由平衡条件得F′OBm=Ffm
又F′OBm=FOBm=m1mgtan θ=m1mg
联立解得m1m===24 kg
即物体甲的质量最大不能超过24 kg.
13.答案(1)mgsin 2θ (2)mgsin 4θ
解析 木块在木楔斜面上匀速向下运动时,有
mgsin θ=μmgcos θ,
即μ=tan θ.
(1)木块在力F作用下沿斜面向上匀速运动,有
Fcos α=mgsin θ+Ff
Fsin α+FN=mgcos θ
Ff=μFN
解得F==
=
则当α=θ时,F有最小值,为Fmin=mgsin 2θ.
(2)因为木块及木楔均处于平衡状态,整体受到地面的摩擦力等于F的水平分力,即
Ff=Fcos(α+θ)
当α=θ时,F取最小值mgsin 2θ,
Ffm=Fmincos 2θ=mg·sin 2θcos 2θ=mgsin 4θ.
