北京市第四中学2021-2022学年七年级上学期开学测试数学试题(Word版 含解析)
文档属性
| 名称 | 北京市第四中学2021-2022学年七年级上学期开学测试数学试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 564.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 07:43:58 | ||
图片预览




文档简介
北京市第四中学2021-2022学年七年级上学期开学测试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.表示一个负数 B.正整数和负整数统称整数
C.表示一个奇数 D.非负数包括零和正数
2.下列式子变形正确的是( )
A.﹣(a﹣1)=﹣a﹣1 B.3a﹣5a=﹣2a
C.2(a+b)=2a+b D.|π﹣3|=3﹣π
3.甲乙两地相距m千米,原计划高速列车每小时行x千米,受天气影响,若实际每小时降速50千米,则列车从甲地到乙地所需时间比原来增加( )小时.
A. B. C. D.
4.天干地支纪年法是中国历法上自古以来就一直使用的纪年方法.天干有十,即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有十二,即:子、丑、寅、卵、辰、巳、午、未、申、酉、戌、亥在天干地支纪年法中,对应的规律如下表:
天干 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 甲 乙 丙 ……
地支 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥 子 ……
干支 纪年 甲 子 年 乙 丑 年 丙 寅 年 丁 卯 年 戊 辰 年 己 巳 年 庚 午 年 辛 未 年 壬 申 年 癸 酉 年 甲 戌 年 乙 亥 年 丙 子 年 ……
2049年是新中国成立100周年这一百年,中国逐步实现中华民族的伟大复兴使用天干地支纪年法,2021年是辛丑年,那么可以推知2049年是( )年
A.乙已 B.己巳 C.己酉 D.乙亥
5.某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入到最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(a>b>c且a,b,c均为正整数);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
二、填空题
6.若某三位数的个位数字为a,十位数字为b,百位数字为c,则此三位数可表示为__________.
7.某小店进了两种不同的果仁,所用的钱一样多,已知两种果仁的价钱分别是每千克6元和12元,若将两种果仁混合后再买,那么,混合后果仁的成本是每千克__________元.
8.某商店将彩电按原价提高了40%,然后在广告中写上“大酬宾,八折优惠”,结果每台彩电比原价多赚了270元,那么每台彩电原价是__________元.
9.循环小数可化分数为__________.
10.时钟上2点到2点30分之间,分针与时针在2点__________分成直角
11.如图,边长为2与3的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是__________(结果保留).
12.如图,平行四边形中,M是边上一点,与对角线交于点N,若,,则__________.
13.日常生活中经常使用十进制来表示数,要用10个数码:0,1,2,3,4,56,7,8,9,在电子计算机中用二进制,只要两个数码0和1,正像在十进制中加法要“逢十进一”,在二进制中必须“逢2进1”,于是,可以得到以下自然数的十进制与二进制表示对照表:
十进制 0 1 2 3 4 5 6 7 8 …
二进制 0 1 10 11 100 101 110 111 1000 …
十进制的0在二进制中还是0,十进制的1在二进制中还是1,十进制的2在二进制中变成了,十进制的3在二进制中变成了,……,那么二进中的110001在十进制中表示的数为__________.
14.如图,在三角形中,,,.为边上的一点,在边上取点,使得,在边上取点,使得,在边上取点,使得,若,则的长度为__________.
15.十九世纪的时候,MorizStern(1858)与AchilleBrocot(1860)发明了“一棵树”,称之为有理数树,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,……,按照这个规律,在第__________层第__________个数(从左往右数).
16.现有一块圆形蛋糕,用刀把它竖着切开.用表示n刀切下去出现的最多的蛋糕块数(,2,3,4…).显然,1刀切下去蛋糕分为两块,记为;2刀切下去蛋糕最多被分为4块,记为;那么__________;与的等量关系为__________;=___________(用含n的式子表示).
17.
三、解答题
18.
19.-0.5-(-3)+2.75-(+7)
20.
21.
22.
23.
24.
25.
26.甲、乙两城相距1120千米,一列快车从甲城出发120千米后,另一列动车从乙城出发开往甲城,2个小时后两车相遇.若快车平均每小时行驶的路程比动车平均每小时行驶的路程的一半还多5千米,动车与快车平均每小时各行驶多少千米?
27.某市为提倡节约用水,采取分段收费.若每户每月用水不超过,每立方米收费2元;若用水超过,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水多少立方米?
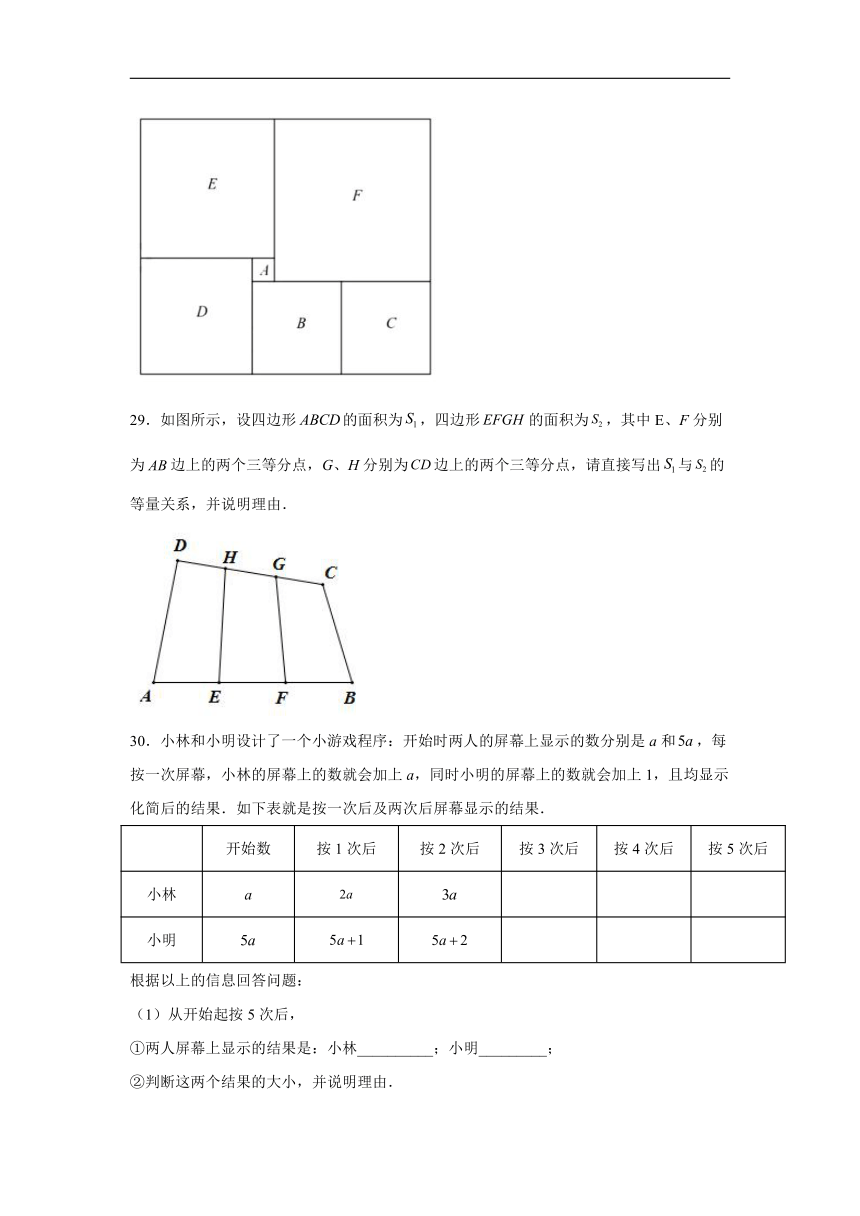
28.如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为2,求这个长方形色块图的面积.
29.如图所示,设四边形的面积为,四边形的面积为,其中E、F分别为边上的两个三等分点,G、H分别为边上的两个三等分点,请直接写出与的等量关系,并说明理由.
30.小林和小明设计了一个小游戏程序:开始时两人的屏幕上显示的数分别是a和,每按一次屏幕,小林的屏幕上的数就会加上a,同时小明的屏幕上的数就会加上1,且均显示化简后的结果.如下表就是按一次后及两次后屏幕显示的结果.
开始数 按1次后 按2次后 按3次后 按4次后 按5次后
小林 a
小明
根据以上的信息回答问题:
(1)从开始起按5次后,
①两人屏幕上显示的结果是:小林__________;小明_________;
②判断这两个结果的大小,并说明理由.
(2)是否存在一个a的值,使得每次按完屏幕后,小林的屏幕上的数,总是小于小明的屏幕上的数,若存在,请直接写出所有满足条件的a的取值范围;若不存在,请说明理由
31.如图,已知图形A,B,C,D,E,F分别是由3,4,5,6,7,8个“单位正方形”(每个小正方形的边长为1)组成的图形,它们之中的五个可以拼成一个大正方形.
(1)填空:能拼成的大正方形的面积等于__________,多余的那一个图形的编号是___________从A,B,C, D,E,F中选择一个)
(2)请在下图中画出拼接正方形的方法,要求:标注所使用五个图形的编号,并用实粗线画出边界线.(说明:所使用的五个图形可以旋转,也可以翻转)
32.大数学家欧拉的数学名著《代数基础》中记录了一个有趣的问题:有一位父亲,临终时嘱咐他的儿子这样来分他的财产;第一个儿子分得100克朗和剩下财产的十分之一;第二个儿子分得200克朗和剩下财产的十分之一﹔第三个儿子分得300克朗和剩下财产的十分之一;第四个儿子分得400克朗和剩下财产的十分之一;……,按这种方法一直分下去,最后,每一个儿子所得财产一样多.问:这位父亲共有几个儿子?每个儿子分得多少财产?
参考答案
1.D
【分析】
根据正负数,整数,奇偶数,非负数的定义判断分析即可求解.
【详解】
解:A、当a<0时,﹣a>0,故本选项错误;
B、整数分正整数、负整数和0,故本选项错误;
C、表示一个奇数,其中n是整数,故本选项错误;
D、非负数包括零和正数,故本选项正确;
故选:D.
【点睛】
本题考查正负数,整数,奇偶数,非负数的定义,解题的关键是熟练掌握并区分以上定义.
2.B
【分析】
根据去括号法则以及合并同类项的定义对各选项依次进行判断即可解答.
【详解】
A.﹣(a﹣1)=﹣a+1,故本选项错误;
B.3a﹣5a=﹣2a,故本选项正确;
C.2(a+b)=2a+2b,故本选项错误;
D.|π﹣3|=π﹣3,故本选项错误.
故选:B.
【点睛】
本题考查了去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是”+“,去括号后,括号里的各项都不改变符号;括号前是”﹣“,去括号后,括号里的各项都改变符号.运用这一法则去掉括号.同时要注意掌握合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
3.C
【分析】
将实际需要减去原计划的时间即可得出从甲地到乙地所增加的时间.
【详解】
解:根据题意得出:
原计划高速列车从甲地到乙地所需时间为:小时,
实际高速列车从甲地到乙地所需时间为:小时,
故列车从甲地到乙地所需时间比原来增加小时,
故选:C.
【点睛】
本题考查代数式的知识,正确解读题意,根据题意得出所求的量是解题的关键.
4.B
【分析】
根据题意,分析干支纪年法的规律,可得天干地支的对应顺序,据此可得2049年是已卯年,即可得答案.
【详解】
根据题意,天干有十,即甲、乙、丙、丁、戊、己、庚、辛、壬、癸,地支有十二,即子、丑、寅、卯、辰、 巳、午、未、申、酉、戌、亥;其相配顺序为:甲子、乙丑、丙寅、...癸酉,甲戌、乙亥、丙子、...癸未,甲申、乙酉、丙戌、...癸巳,...
若2021年是辛丑年,从2021年往后数28年,可得2049年是己巳年.
故选:B.
【点睛】
本题考查合情推理的应用,解题的关键是掌握“干支纪年法"的规律,属于基础题.
5.C
【分析】
根据四场比赛总得分,结合a,b,c满足的条件,可求出a,b,c,再根据已知的得分情况,确定甲、乙、丙的得分情况,问题即可解决.
【详解】
解:∵甲最后得分为16分,
∴a>4,
接下来以乙为主要研究对象,
①若乙得分名次为:1场第一名,3场第二名,则a+3b=8,
则3b=8﹣a<4,而b为正整数,
则b=1,又c为正整数,a>b>c,
此时不合题意;
②若乙得分名次为:1场第一名,2场第二名,1场第三名,
则a+2b+c=8,
则2b+c=8﹣a<4,
由a>b>c,且a,b,c为正整数可知,
此时没有符合该不等式的解,
不符合题意;
③若乙得分名次为:1场第一名,1场第二名,2场第三名,
则a+b+2c=8,则b+2c=8﹣a<4,
由a>b>c,且a,b,c为正整数可知,
此时没有符合该不等式的解,不符合题意;
④若乙得分名次为:1场第一名,3场第三名,
则a+3c=8,此时显然a=5,c=1,
则甲的得分情况为3场第一名,1场第三名,共3×5+1=16分,
乙的得分情况为1场第一名,3场第三名,共5+3×1=8分,
丙的得分情况为4场第二名,则4b=8,即b=2,
此时符合题意.
综上分析可知,乙在四场比赛中没有获得过第二名.
故选:C.
【点睛】
本题考查了合情推理的问题,考查了推理论证能力,考查了化归与转化思想,审清题意是正确解题的关键,属于中档题.
6.
【分析】
根据是三位数=百位上的数字×100+十位上的数字×10+个位上的数字进行解答即可.
【详解】
解:根据题意,这个三位数可以表示为100a+10b+c,
故答案为:100a+10b+c.
【点睛】
本题考查列代数式,掌握三位数的表示方法是解答的关键.
7.8
【分析】
先根据题意可得到每千克6元和12元的果仁数量之比为2:1,然后得到混合后果仁的成本是每千克为,即可求解.
【详解】
解:∵进了两种不同的果仁,所用的钱一样多,已知两种果仁的价钱分别是每千克6元和12元,
∴每千克6元和12元的果仁数量之比为:
,
∴混合后果仁的成本是每千克为 (元).
故答案为:8.
【点睛】
本题主要考查了有理数的运算的实际应用,理解题意,得到每千克6元和12元的果仁数量之比为2:1是解题的关键.
8.2250
【分析】
设出每台彩电的原价,从而可得方程,即可求得结论.
【详解】
解:设每台彩电的原价是x,则
,
解得:,
故答案为:2250.
【点睛】
本题考查一元一次方程的应用,关键在于找出题目中的等量关系,根据等量关系列出方程解答.
9.
【分析】
x=,方程两边都乘以100,转化为15+x=100x,求出其解即可.
【详解】
设x=,即x=0.1515…,
将方程两边都乘以100,得100x=15.1515…,
即100x=15+0.1515…,又因为x=0.1515…,
所以100x=15+x,所以99x=15,即x=,
所以=
故答案为:.
【点睛】
本题考查了无限循环小数转化为分数,运用一元一次方程解实际问题的应用,解答时根据等式的性质变形建立方程是解答的关键.
10.
【分析】
根据对钟表的认识,可得时针每分钟走0.5度,而分针每分钟走6度,设2点x分,时针和分针所成的角度为90°,根据题意列出方程,即可得出答案.
【详解】
∵2点时,时针和分针所成的角度为60°
∴分针与时针成90时,分针追赶了时针150°
设2点x分,时针和分针所成的角度为90°,
依题意可得6x-0.5x=150
解得x=
故答案为:.
【点睛】
本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:时针每分钟走0.5度,而分针每分钟走6度,并且利用起点时间时针和分针的位置关系建立角的图形.转化为方程解决.
11.
【分析】
如图,根据图形有,然后根据扇形、梯形和三角形的面积公式进行计算即可.
【详解】
如图,正方形BEFG的边长是2,正方形ABCD的边长是3,
,
根据题意,
,
,
,
,
故答案为:.
【点睛】
本题考查了扇形的面积公式,也考查了梯形和三角形的面积公式以及不规则几何图形面积的求法.
12.
【分析】
由S△ABN=4,S△BMN=3可求出AN:NM的值,根据△AND∽△MNB,继而得出AN:NM=DN:NB=4:3,然后根据面积比等于相似比的平方,可求出S△AND.
【详解】
∵ANB和△BMN同高,S△ABN=4,S△BMN=3,
∴AN:NM=4:3,
又∵
∴△AND∽△MNB,
∴DN:NB=AN:NM=4:3,
∴,
∴S△AND=,
故答案为:.
【点睛】
本题考查了面积及等积变换的知识,要求我们掌握平行四边形的性质及同一底边上等高的三角形面积之比等于底边之比,相似三角形的面积之比等于相似比的平方,难度中等.
13.49
【分析】
二进制中10表示成十进制数是=2;二进制中11表示成十进制数是=3;二进制中100表示成十进制数是=4;二进制中101表示成十进制数是=5;二进制中110表示成十进制数是=6;以此类推,求出110001换算成十进制的数字.
【详解】
故答案为49
【点睛】
本题考查二进制与十进制数的互化方法,掌握转化公式是解题的关键.
14.5或6
【分析】
根据题意,可以设CP0的长度为x,列出相应的方程,然后利用分类讨论的方法即可求得CP0的长度.
【详解】
如图,
设CP0=x,则CP1=x,AP1=9-x=AP2,BP2=8-(9-x)=x-1=BP3,
若点 在 、 两点之间,即BP3+CP0+1=BC=10时,
(x-1)+x+1=10,解得,x=5;
若点 在 、两点之间,即BP3+CP0-1=BC=10时,
(x-1)+x-1=10,解得,x=6.
故答案为:5或6.
【点睛】
本题主要考查一元一次方程的应用,解答本题的关键是明确题意,利用方程和分类讨论的方法解答.
15.10 253
【分析】
由图可知,向右发散的都是真分数,规律为,向左发散的都是假分数,规律是,据此逆推可得所在的层数,再根据每一层数的位置确定所在的具体位置
【详解】
设在第层,则第层的与连线的数为:,层与之连线的数为:;…,则在第层
由图可知,
从第3层至第8层数字都是向左边发散,第9,10层的数字是向右发散,即:
的左边有1个数,
的左边有3个数,
的左边有7个数,
的左边有15个数,
的左边有31个数,
的左边有63个数,
是上一层数字向右发散的,故左侧多1个数,的左边有个数,
是上一层数字向右发散的,故左侧多2个数,的左边有个数,
和是在同一层,且在的左侧,
从左往右数,是第个数,
故答案为:
【点睛】
本题考查了数字类型规律,找到左右发散的数字的规律是解题的关键.
16.7 .
【分析】
(1)当1刀切下去蛋糕分为两块,记为; 2刀切下去蛋糕最多被分为4块,记为=1+1+2=4; 3刀切下去蛋糕分为: 1+1+2+3=7;
(2)观察发现,切2刀时比原来多了2块,切3刀时比原来多了3块,…,切n刀时比原来多了n块,切 (n+1)刀时比原来多了(n+1)块;
(3)当切1刀时,; 切2刀时,=1+1+2=4;切2刀时,平面数 1+1+2+3=7; …切5刀时,=1+1+2+3+4+5;切6刀时,=1+1+2+3+4+5+6,计算即可; =1+1+2+3…+n,整理即可.
【详解】
(1)解:1刀切下去蛋糕分为两块,记为;
2刀切下去蛋糕最多被分为4块,记为=1+1+2=4;
3刀切下去蛋糕分为: 1+1+2+3=7;
故答案为:;
(2)观察发现:
切2刀时比原来多了2块,
切3刀时比原来多了3块,…,
切n刀时比原来多了n块,
切 (n+1)刀时比原来多了(n+1)块;
故答案为:;
(3)当切1刀时,;
切2刀时,=1+1+2=4;
切2刀时,平面数 1+1+2+3=7; …
切5刀时,=1+1+2+3+4+5;
切6刀时,=1+1+2+3+4+5+6,
切n刀时,=1+1+2+3…+n=1+=.
故答案为: 7,,.
【点睛】
本题主要考查图形变化规律性问题,解决本题的关键是要观察归纳总结图形变化规律.
17.1020605
【分析】
先根据算式找规律,把同分母的分数合成一组,然后根据高斯求和公式解答即可.
【详解】
解:
.
【点睛】
本题考查了分数的巧算,解题的关键是把分数分组,难点是利用高斯求和公式求出分子.
18.
【分析】
先通分,再进行有理数的加法运算即可求解.
【详解】
解:.
【点睛】
本题考查了有理数的加法运算,熟练掌握有理数的加法运算法则是解题的关键,注意异分母的分数相加减要先通分再计算.
19.-2
【分析】
首先将同分母的进行合并计算,然后进行有理数的加减法计算
【详解】
解:原式==-8+6=-2
考点:有理数的计算
20.
【分析】
分数加减乘除的混合运算,先算小括号,再算中括号.
【详解】
故答案为-1
【点睛】
本题考查分数的混合运算,掌握运算次序是关键,有括号按小括号,中括号,大括号的顺序;不同级别的算式按先乘除后加减的顺序;同一级别按照从左至右的顺序.
21.
【分析】
根据乘法分配律即可解答.
【详解】
,
,
,
,
.
【点睛】
本题考查的是有理数的混合运算,解题关键是明确有理数混合运算的计算方法.
22.25
【分析】
根据有理数的运算法则即可求解.
【详解】
=
=
=25.
【点睛】
此题主要考查有理数的运算,解题的关键是熟知有理数的简便运算法则.
23.1
【分析】
根据有理数的混合运算法则即可求解.
【详解】
=
=
=1.
【点睛】
此题主要考查有理数的混合运算,解题的关键是熟知其运算法则.
24.2023
【分析】
先提出分子中的公因数 ,再将分子中的2022化为 ,分母中的 化为 ,然后分子分母局部再提公因数,即可求解.
【详解】
解:
.
【点睛】
本题主要考查了有理数混合运算,能提出公因数将分子分母进行变形是解题的关键.
25.
【分析】
本题算式较长,如果按部就班去做,根本不可能,就要寻求简单的做法.为了计算方便,先把分子固定,把分母写成两个连续的数字相乘的形式,进而变成分数加减的形式,通过前后相互抵消快速得出结果.
【详解】
原式=
=
=
=
=
=
=
=
故答案为
【点睛】
本题实际考查裂项相消法的灵活应用,不能直接裂项的先想办法构造可以裂项的形式,再套用裂项的方法即可快速得出答案.
26.动车平均每小时行驶330千米,快车平均每小时行驶170千米
【分析】
首先设动车平均每小时行驶v千米,快车平均每小时行驶v千米,根据题意列出方程,求出即可.
【详解】
解:设动车平均每小时行驶v千米,快车平均每小时行驶v千米.则
,
,
解得,.
所以动车平均每小时行驶330千米,快车平均每小时行驶170千米.
【点睛】
本题考查了一元一次方程的应用,培养了学生应用数学解决生活中实际问题的能力,根据已知表示出两车行驶的路程是解题关键.
27.28
【分析】
设小明家5月份用水xm3,先求出用水量为20m3时应交水费,与64比较后即可得出x>20,再根据应交水费=40+3×超过20m3部分即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
解:设小明家5月份用水xm3, 当用水量为20m3时,
应交水费为20×2=40(元).
∵40<64,
∴x>20.
根据题意得:40+(2+1)(x-20)=64, 解得:x=28.
答:小明家用水28立方米.
【点评】
本题主要考查了一元一次方程的应用,解决本题的关键是要认真审题确定等量关系.
28.572
【分析】
设D边长为x,则B、C边长,E边长,F边长,根据题意列出关于x的一元一次方程,求出x的值,再根据面积公式即可求出答案.
【详解】
解:设D边长为x,则B、C边长,E边长,F边长.
由题意可得:,
解得.
故长方形的长为26,宽为22,面积为.
【点睛】
考查了一元一次方程的应用,其中涉及到了矩形的性质,正方形的性质和面积公式等知识点,解此题的关键是正确设未知数并列出方程.
29.,理由见解析.
【分析】
如图连结、、,然后根据三角形等底等高得到,,进而得到,然后再说明即可解答.
【详解】
解:,理由如下:
连结DE、EG、GB、BD,则:S△BDE=S△BAD,S△BDG=S△BCD,S△EHG=S△EHD,S△BGF=S△EGF,
∴SDEBG=SABCD=S1,
又∵S△EHG=S△EHD,S△BGF=S△EGF,
∴SEFHG=SDEBG=S1,
∴S2=S1,即.
【点睛】
本题主要考查了三角形的等分点以及三角形的面积, 掌握等底等高三角形的面积关系是解答本题的关键.
30.(1)①;;②若,则;若,则;若,则;理由见解析;(2) 存在,
【分析】
(1)①根据每按一次屏幕,小林的频幕上的数就会加上a,同时小明的屏幕上的数就会加上1,求解即可;
②作差得出结果,根据结果讨论即可;
(2)根据按1次后小林数字小于小明屏幕上的数列不等式,然后根据数字变化规律可得小林往后每按一次增加的数必须小于等于小明每按一次增加的数,由此可得结论.
【详解】
解:(1)根据每按一次屏幕,小林的频幕上的数就会加上a,
同时小明的屏幕上的数就会加上1,则从开始起按5次后,
小林:,小明:,
故答案为:;;
②作差,
∴若,即,则;
若,即,则:
若,即,则.
(2)存在,理由如下:
∵小林的屏幕上的数,总是小于小明的屏幕上的数,
∴,
解得:,
∵每按一次屏幕,小林的频幕上的数就会加上a,
同时小明的屏幕上的数就会加上1,
∴要想保持小林的屏幕上的数,总是小于小明的屏幕上的数,
必须满足,
综上:.
【点睛】
本题考查了列代数式,解题的关键是理解题意,找出数字变化规律.
31.(1)25,F;(2)见解析
【分析】
(1)根据给出的图形A,B,C,D,E,F的面积可知和在25和33之间,进而得到组成大正方形的小正方形数量25个;F是多余的;
(2)把图形A,B,C,D,E,F或旋转或翻转,拼接即可.
【详解】
(1)组成大正方形的小正方形数量可能是1、4、9、16、25、36…
而3+4+5+6+7+8=33在25和36之间,
所以组成大正方形的小正方形数量25个,多余8个.
故答案为:25,F.
(2)如图所示.
【点睛】
本题考查了利用旋转变换作图,正方体的性质,熟记正方形的性质是解题的关键.
32.9;900
【分析】
设遗产总数为克朗,根据题意可表示出第一个和第二个儿子分别获得的遗产,然后根据每个儿子分得一样多列出一元一次方程,从而求出总的遗产数,由此可得第一个儿子获得的遗产,即可得到每个儿子获得的遗产,从而求出总人数即可.
【详解】
解:设遗产总数为克朗,则:
第一个儿子分得:;
第二个儿子分得:;
∵每一个儿子所得财产一样多,
∴,
解得:,
∴遗产共有8100克朗,
则第一个儿子分得:(克朗),
即:每个儿子分得900克朗,
儿子共有:(人),
∴这位父亲共有9个儿子,每个儿子分得900克朗.
【点睛】
本题考查一元一次方程的实际应用,理解题意,准确设出未知数,并建立方程求解是解题关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.表示一个负数 B.正整数和负整数统称整数
C.表示一个奇数 D.非负数包括零和正数
2.下列式子变形正确的是( )
A.﹣(a﹣1)=﹣a﹣1 B.3a﹣5a=﹣2a
C.2(a+b)=2a+b D.|π﹣3|=3﹣π
3.甲乙两地相距m千米,原计划高速列车每小时行x千米,受天气影响,若实际每小时降速50千米,则列车从甲地到乙地所需时间比原来增加( )小时.
A. B. C. D.
4.天干地支纪年法是中国历法上自古以来就一直使用的纪年方法.天干有十,即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有十二,即:子、丑、寅、卵、辰、巳、午、未、申、酉、戌、亥在天干地支纪年法中,对应的规律如下表:
天干 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 甲 乙 丙 ……
地支 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥 子 ……
干支 纪年 甲 子 年 乙 丑 年 丙 寅 年 丁 卯 年 戊 辰 年 己 巳 年 庚 午 年 辛 未 年 壬 申 年 癸 酉 年 甲 戌 年 乙 亥 年 丙 子 年 ……
2049年是新中国成立100周年这一百年,中国逐步实现中华民族的伟大复兴使用天干地支纪年法,2021年是辛丑年,那么可以推知2049年是( )年
A.乙已 B.己巳 C.己酉 D.乙亥
5.某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入到最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(a>b>c且a,b,c均为正整数);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
二、填空题
6.若某三位数的个位数字为a,十位数字为b,百位数字为c,则此三位数可表示为__________.
7.某小店进了两种不同的果仁,所用的钱一样多,已知两种果仁的价钱分别是每千克6元和12元,若将两种果仁混合后再买,那么,混合后果仁的成本是每千克__________元.
8.某商店将彩电按原价提高了40%,然后在广告中写上“大酬宾,八折优惠”,结果每台彩电比原价多赚了270元,那么每台彩电原价是__________元.
9.循环小数可化分数为__________.
10.时钟上2点到2点30分之间,分针与时针在2点__________分成直角
11.如图,边长为2与3的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是__________(结果保留).
12.如图,平行四边形中,M是边上一点,与对角线交于点N,若,,则__________.
13.日常生活中经常使用十进制来表示数,要用10个数码:0,1,2,3,4,56,7,8,9,在电子计算机中用二进制,只要两个数码0和1,正像在十进制中加法要“逢十进一”,在二进制中必须“逢2进1”,于是,可以得到以下自然数的十进制与二进制表示对照表:
十进制 0 1 2 3 4 5 6 7 8 …
二进制 0 1 10 11 100 101 110 111 1000 …
十进制的0在二进制中还是0,十进制的1在二进制中还是1,十进制的2在二进制中变成了,十进制的3在二进制中变成了,……,那么二进中的110001在十进制中表示的数为__________.
14.如图,在三角形中,,,.为边上的一点,在边上取点,使得,在边上取点,使得,在边上取点,使得,若,则的长度为__________.
15.十九世纪的时候,MorizStern(1858)与AchilleBrocot(1860)发明了“一棵树”,称之为有理数树,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,……,按照这个规律,在第__________层第__________个数(从左往右数).
16.现有一块圆形蛋糕,用刀把它竖着切开.用表示n刀切下去出现的最多的蛋糕块数(,2,3,4…).显然,1刀切下去蛋糕分为两块,记为;2刀切下去蛋糕最多被分为4块,记为;那么__________;与的等量关系为__________;=___________(用含n的式子表示).
17.
三、解答题
18.
19.-0.5-(-3)+2.75-(+7)
20.
21.
22.
23.
24.
25.
26.甲、乙两城相距1120千米,一列快车从甲城出发120千米后,另一列动车从乙城出发开往甲城,2个小时后两车相遇.若快车平均每小时行驶的路程比动车平均每小时行驶的路程的一半还多5千米,动车与快车平均每小时各行驶多少千米?
27.某市为提倡节约用水,采取分段收费.若每户每月用水不超过,每立方米收费2元;若用水超过,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水多少立方米?
28.如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为2,求这个长方形色块图的面积.
29.如图所示,设四边形的面积为,四边形的面积为,其中E、F分别为边上的两个三等分点,G、H分别为边上的两个三等分点,请直接写出与的等量关系,并说明理由.
30.小林和小明设计了一个小游戏程序:开始时两人的屏幕上显示的数分别是a和,每按一次屏幕,小林的屏幕上的数就会加上a,同时小明的屏幕上的数就会加上1,且均显示化简后的结果.如下表就是按一次后及两次后屏幕显示的结果.
开始数 按1次后 按2次后 按3次后 按4次后 按5次后
小林 a
小明
根据以上的信息回答问题:
(1)从开始起按5次后,
①两人屏幕上显示的结果是:小林__________;小明_________;
②判断这两个结果的大小,并说明理由.
(2)是否存在一个a的值,使得每次按完屏幕后,小林的屏幕上的数,总是小于小明的屏幕上的数,若存在,请直接写出所有满足条件的a的取值范围;若不存在,请说明理由
31.如图,已知图形A,B,C,D,E,F分别是由3,4,5,6,7,8个“单位正方形”(每个小正方形的边长为1)组成的图形,它们之中的五个可以拼成一个大正方形.
(1)填空:能拼成的大正方形的面积等于__________,多余的那一个图形的编号是___________从A,B,C, D,E,F中选择一个)
(2)请在下图中画出拼接正方形的方法,要求:标注所使用五个图形的编号,并用实粗线画出边界线.(说明:所使用的五个图形可以旋转,也可以翻转)
32.大数学家欧拉的数学名著《代数基础》中记录了一个有趣的问题:有一位父亲,临终时嘱咐他的儿子这样来分他的财产;第一个儿子分得100克朗和剩下财产的十分之一;第二个儿子分得200克朗和剩下财产的十分之一﹔第三个儿子分得300克朗和剩下财产的十分之一;第四个儿子分得400克朗和剩下财产的十分之一;……,按这种方法一直分下去,最后,每一个儿子所得财产一样多.问:这位父亲共有几个儿子?每个儿子分得多少财产?
参考答案
1.D
【分析】
根据正负数,整数,奇偶数,非负数的定义判断分析即可求解.
【详解】
解:A、当a<0时,﹣a>0,故本选项错误;
B、整数分正整数、负整数和0,故本选项错误;
C、表示一个奇数,其中n是整数,故本选项错误;
D、非负数包括零和正数,故本选项正确;
故选:D.
【点睛】
本题考查正负数,整数,奇偶数,非负数的定义,解题的关键是熟练掌握并区分以上定义.
2.B
【分析】
根据去括号法则以及合并同类项的定义对各选项依次进行判断即可解答.
【详解】
A.﹣(a﹣1)=﹣a+1,故本选项错误;
B.3a﹣5a=﹣2a,故本选项正确;
C.2(a+b)=2a+2b,故本选项错误;
D.|π﹣3|=π﹣3,故本选项错误.
故选:B.
【点睛】
本题考查了去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是”+“,去括号后,括号里的各项都不改变符号;括号前是”﹣“,去括号后,括号里的各项都改变符号.运用这一法则去掉括号.同时要注意掌握合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
3.C
【分析】
将实际需要减去原计划的时间即可得出从甲地到乙地所增加的时间.
【详解】
解:根据题意得出:
原计划高速列车从甲地到乙地所需时间为:小时,
实际高速列车从甲地到乙地所需时间为:小时,
故列车从甲地到乙地所需时间比原来增加小时,
故选:C.
【点睛】
本题考查代数式的知识,正确解读题意,根据题意得出所求的量是解题的关键.
4.B
【分析】
根据题意,分析干支纪年法的规律,可得天干地支的对应顺序,据此可得2049年是已卯年,即可得答案.
【详解】
根据题意,天干有十,即甲、乙、丙、丁、戊、己、庚、辛、壬、癸,地支有十二,即子、丑、寅、卯、辰、 巳、午、未、申、酉、戌、亥;其相配顺序为:甲子、乙丑、丙寅、...癸酉,甲戌、乙亥、丙子、...癸未,甲申、乙酉、丙戌、...癸巳,...
若2021年是辛丑年,从2021年往后数28年,可得2049年是己巳年.
故选:B.
【点睛】
本题考查合情推理的应用,解题的关键是掌握“干支纪年法"的规律,属于基础题.
5.C
【分析】
根据四场比赛总得分,结合a,b,c满足的条件,可求出a,b,c,再根据已知的得分情况,确定甲、乙、丙的得分情况,问题即可解决.
【详解】
解:∵甲最后得分为16分,
∴a>4,
接下来以乙为主要研究对象,
①若乙得分名次为:1场第一名,3场第二名,则a+3b=8,
则3b=8﹣a<4,而b为正整数,
则b=1,又c为正整数,a>b>c,
此时不合题意;
②若乙得分名次为:1场第一名,2场第二名,1场第三名,
则a+2b+c=8,
则2b+c=8﹣a<4,
由a>b>c,且a,b,c为正整数可知,
此时没有符合该不等式的解,
不符合题意;
③若乙得分名次为:1场第一名,1场第二名,2场第三名,
则a+b+2c=8,则b+2c=8﹣a<4,
由a>b>c,且a,b,c为正整数可知,
此时没有符合该不等式的解,不符合题意;
④若乙得分名次为:1场第一名,3场第三名,
则a+3c=8,此时显然a=5,c=1,
则甲的得分情况为3场第一名,1场第三名,共3×5+1=16分,
乙的得分情况为1场第一名,3场第三名,共5+3×1=8分,
丙的得分情况为4场第二名,则4b=8,即b=2,
此时符合题意.
综上分析可知,乙在四场比赛中没有获得过第二名.
故选:C.
【点睛】
本题考查了合情推理的问题,考查了推理论证能力,考查了化归与转化思想,审清题意是正确解题的关键,属于中档题.
6.
【分析】
根据是三位数=百位上的数字×100+十位上的数字×10+个位上的数字进行解答即可.
【详解】
解:根据题意,这个三位数可以表示为100a+10b+c,
故答案为:100a+10b+c.
【点睛】
本题考查列代数式,掌握三位数的表示方法是解答的关键.
7.8
【分析】
先根据题意可得到每千克6元和12元的果仁数量之比为2:1,然后得到混合后果仁的成本是每千克为,即可求解.
【详解】
解:∵进了两种不同的果仁,所用的钱一样多,已知两种果仁的价钱分别是每千克6元和12元,
∴每千克6元和12元的果仁数量之比为:
,
∴混合后果仁的成本是每千克为 (元).
故答案为:8.
【点睛】
本题主要考查了有理数的运算的实际应用,理解题意,得到每千克6元和12元的果仁数量之比为2:1是解题的关键.
8.2250
【分析】
设出每台彩电的原价,从而可得方程,即可求得结论.
【详解】
解:设每台彩电的原价是x,则
,
解得:,
故答案为:2250.
【点睛】
本题考查一元一次方程的应用,关键在于找出题目中的等量关系,根据等量关系列出方程解答.
9.
【分析】
x=,方程两边都乘以100,转化为15+x=100x,求出其解即可.
【详解】
设x=,即x=0.1515…,
将方程两边都乘以100,得100x=15.1515…,
即100x=15+0.1515…,又因为x=0.1515…,
所以100x=15+x,所以99x=15,即x=,
所以=
故答案为:.
【点睛】
本题考查了无限循环小数转化为分数,运用一元一次方程解实际问题的应用,解答时根据等式的性质变形建立方程是解答的关键.
10.
【分析】
根据对钟表的认识,可得时针每分钟走0.5度,而分针每分钟走6度,设2点x分,时针和分针所成的角度为90°,根据题意列出方程,即可得出答案.
【详解】
∵2点时,时针和分针所成的角度为60°
∴分针与时针成90时,分针追赶了时针150°
设2点x分,时针和分针所成的角度为90°,
依题意可得6x-0.5x=150
解得x=
故答案为:.
【点睛】
本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:时针每分钟走0.5度,而分针每分钟走6度,并且利用起点时间时针和分针的位置关系建立角的图形.转化为方程解决.
11.
【分析】
如图,根据图形有,然后根据扇形、梯形和三角形的面积公式进行计算即可.
【详解】
如图,正方形BEFG的边长是2,正方形ABCD的边长是3,
,
根据题意,
,
,
,
,
故答案为:.
【点睛】
本题考查了扇形的面积公式,也考查了梯形和三角形的面积公式以及不规则几何图形面积的求法.
12.
【分析】
由S△ABN=4,S△BMN=3可求出AN:NM的值,根据△AND∽△MNB,继而得出AN:NM=DN:NB=4:3,然后根据面积比等于相似比的平方,可求出S△AND.
【详解】
∵ANB和△BMN同高,S△ABN=4,S△BMN=3,
∴AN:NM=4:3,
又∵
∴△AND∽△MNB,
∴DN:NB=AN:NM=4:3,
∴,
∴S△AND=,
故答案为:.
【点睛】
本题考查了面积及等积变换的知识,要求我们掌握平行四边形的性质及同一底边上等高的三角形面积之比等于底边之比,相似三角形的面积之比等于相似比的平方,难度中等.
13.49
【分析】
二进制中10表示成十进制数是=2;二进制中11表示成十进制数是=3;二进制中100表示成十进制数是=4;二进制中101表示成十进制数是=5;二进制中110表示成十进制数是=6;以此类推,求出110001换算成十进制的数字.
【详解】
故答案为49
【点睛】
本题考查二进制与十进制数的互化方法,掌握转化公式是解题的关键.
14.5或6
【分析】
根据题意,可以设CP0的长度为x,列出相应的方程,然后利用分类讨论的方法即可求得CP0的长度.
【详解】
如图,
设CP0=x,则CP1=x,AP1=9-x=AP2,BP2=8-(9-x)=x-1=BP3,
若点 在 、 两点之间,即BP3+CP0+1=BC=10时,
(x-1)+x+1=10,解得,x=5;
若点 在 、两点之间,即BP3+CP0-1=BC=10时,
(x-1)+x-1=10,解得,x=6.
故答案为:5或6.
【点睛】
本题主要考查一元一次方程的应用,解答本题的关键是明确题意,利用方程和分类讨论的方法解答.
15.10 253
【分析】
由图可知,向右发散的都是真分数,规律为,向左发散的都是假分数,规律是,据此逆推可得所在的层数,再根据每一层数的位置确定所在的具体位置
【详解】
设在第层,则第层的与连线的数为:,层与之连线的数为:;…,则在第层
由图可知,
从第3层至第8层数字都是向左边发散,第9,10层的数字是向右发散,即:
的左边有1个数,
的左边有3个数,
的左边有7个数,
的左边有15个数,
的左边有31个数,
的左边有63个数,
是上一层数字向右发散的,故左侧多1个数,的左边有个数,
是上一层数字向右发散的,故左侧多2个数,的左边有个数,
和是在同一层,且在的左侧,
从左往右数,是第个数,
故答案为:
【点睛】
本题考查了数字类型规律,找到左右发散的数字的规律是解题的关键.
16.7 .
【分析】
(1)当1刀切下去蛋糕分为两块,记为; 2刀切下去蛋糕最多被分为4块,记为=1+1+2=4; 3刀切下去蛋糕分为: 1+1+2+3=7;
(2)观察发现,切2刀时比原来多了2块,切3刀时比原来多了3块,…,切n刀时比原来多了n块,切 (n+1)刀时比原来多了(n+1)块;
(3)当切1刀时,; 切2刀时,=1+1+2=4;切2刀时,平面数 1+1+2+3=7; …切5刀时,=1+1+2+3+4+5;切6刀时,=1+1+2+3+4+5+6,计算即可; =1+1+2+3…+n,整理即可.
【详解】
(1)解:1刀切下去蛋糕分为两块,记为;
2刀切下去蛋糕最多被分为4块,记为=1+1+2=4;
3刀切下去蛋糕分为: 1+1+2+3=7;
故答案为:;
(2)观察发现:
切2刀时比原来多了2块,
切3刀时比原来多了3块,…,
切n刀时比原来多了n块,
切 (n+1)刀时比原来多了(n+1)块;
故答案为:;
(3)当切1刀时,;
切2刀时,=1+1+2=4;
切2刀时,平面数 1+1+2+3=7; …
切5刀时,=1+1+2+3+4+5;
切6刀时,=1+1+2+3+4+5+6,
切n刀时,=1+1+2+3…+n=1+=.
故答案为: 7,,.
【点睛】
本题主要考查图形变化规律性问题,解决本题的关键是要观察归纳总结图形变化规律.
17.1020605
【分析】
先根据算式找规律,把同分母的分数合成一组,然后根据高斯求和公式解答即可.
【详解】
解:
.
【点睛】
本题考查了分数的巧算,解题的关键是把分数分组,难点是利用高斯求和公式求出分子.
18.
【分析】
先通分,再进行有理数的加法运算即可求解.
【详解】
解:.
【点睛】
本题考查了有理数的加法运算,熟练掌握有理数的加法运算法则是解题的关键,注意异分母的分数相加减要先通分再计算.
19.-2
【分析】
首先将同分母的进行合并计算,然后进行有理数的加减法计算
【详解】
解:原式==-8+6=-2
考点:有理数的计算
20.
【分析】
分数加减乘除的混合运算,先算小括号,再算中括号.
【详解】
故答案为-1
【点睛】
本题考查分数的混合运算,掌握运算次序是关键,有括号按小括号,中括号,大括号的顺序;不同级别的算式按先乘除后加减的顺序;同一级别按照从左至右的顺序.
21.
【分析】
根据乘法分配律即可解答.
【详解】
,
,
,
,
.
【点睛】
本题考查的是有理数的混合运算,解题关键是明确有理数混合运算的计算方法.
22.25
【分析】
根据有理数的运算法则即可求解.
【详解】
=
=
=25.
【点睛】
此题主要考查有理数的运算,解题的关键是熟知有理数的简便运算法则.
23.1
【分析】
根据有理数的混合运算法则即可求解.
【详解】
=
=
=1.
【点睛】
此题主要考查有理数的混合运算,解题的关键是熟知其运算法则.
24.2023
【分析】
先提出分子中的公因数 ,再将分子中的2022化为 ,分母中的 化为 ,然后分子分母局部再提公因数,即可求解.
【详解】
解:
.
【点睛】
本题主要考查了有理数混合运算,能提出公因数将分子分母进行变形是解题的关键.
25.
【分析】
本题算式较长,如果按部就班去做,根本不可能,就要寻求简单的做法.为了计算方便,先把分子固定,把分母写成两个连续的数字相乘的形式,进而变成分数加减的形式,通过前后相互抵消快速得出结果.
【详解】
原式=
=
=
=
=
=
=
=
故答案为
【点睛】
本题实际考查裂项相消法的灵活应用,不能直接裂项的先想办法构造可以裂项的形式,再套用裂项的方法即可快速得出答案.
26.动车平均每小时行驶330千米,快车平均每小时行驶170千米
【分析】
首先设动车平均每小时行驶v千米,快车平均每小时行驶v千米,根据题意列出方程,求出即可.
【详解】
解:设动车平均每小时行驶v千米,快车平均每小时行驶v千米.则
,
,
解得,.
所以动车平均每小时行驶330千米,快车平均每小时行驶170千米.
【点睛】
本题考查了一元一次方程的应用,培养了学生应用数学解决生活中实际问题的能力,根据已知表示出两车行驶的路程是解题关键.
27.28
【分析】
设小明家5月份用水xm3,先求出用水量为20m3时应交水费,与64比较后即可得出x>20,再根据应交水费=40+3×超过20m3部分即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
解:设小明家5月份用水xm3, 当用水量为20m3时,
应交水费为20×2=40(元).
∵40<64,
∴x>20.
根据题意得:40+(2+1)(x-20)=64, 解得:x=28.
答:小明家用水28立方米.
【点评】
本题主要考查了一元一次方程的应用,解决本题的关键是要认真审题确定等量关系.
28.572
【分析】
设D边长为x,则B、C边长,E边长,F边长,根据题意列出关于x的一元一次方程,求出x的值,再根据面积公式即可求出答案.
【详解】
解:设D边长为x,则B、C边长,E边长,F边长.
由题意可得:,
解得.
故长方形的长为26,宽为22,面积为.
【点睛】
考查了一元一次方程的应用,其中涉及到了矩形的性质,正方形的性质和面积公式等知识点,解此题的关键是正确设未知数并列出方程.
29.,理由见解析.
【分析】
如图连结、、,然后根据三角形等底等高得到,,进而得到,然后再说明即可解答.
【详解】
解:,理由如下:
连结DE、EG、GB、BD,则:S△BDE=S△BAD,S△BDG=S△BCD,S△EHG=S△EHD,S△BGF=S△EGF,
∴SDEBG=SABCD=S1,
又∵S△EHG=S△EHD,S△BGF=S△EGF,
∴SEFHG=SDEBG=S1,
∴S2=S1,即.
【点睛】
本题主要考查了三角形的等分点以及三角形的面积, 掌握等底等高三角形的面积关系是解答本题的关键.
30.(1)①;;②若,则;若,则;若,则;理由见解析;(2) 存在,
【分析】
(1)①根据每按一次屏幕,小林的频幕上的数就会加上a,同时小明的屏幕上的数就会加上1,求解即可;
②作差得出结果,根据结果讨论即可;
(2)根据按1次后小林数字小于小明屏幕上的数列不等式,然后根据数字变化规律可得小林往后每按一次增加的数必须小于等于小明每按一次增加的数,由此可得结论.
【详解】
解:(1)根据每按一次屏幕,小林的频幕上的数就会加上a,
同时小明的屏幕上的数就会加上1,则从开始起按5次后,
小林:,小明:,
故答案为:;;
②作差,
∴若,即,则;
若,即,则:
若,即,则.
(2)存在,理由如下:
∵小林的屏幕上的数,总是小于小明的屏幕上的数,
∴,
解得:,
∵每按一次屏幕,小林的频幕上的数就会加上a,
同时小明的屏幕上的数就会加上1,
∴要想保持小林的屏幕上的数,总是小于小明的屏幕上的数,
必须满足,
综上:.
【点睛】
本题考查了列代数式,解题的关键是理解题意,找出数字变化规律.
31.(1)25,F;(2)见解析
【分析】
(1)根据给出的图形A,B,C,D,E,F的面积可知和在25和33之间,进而得到组成大正方形的小正方形数量25个;F是多余的;
(2)把图形A,B,C,D,E,F或旋转或翻转,拼接即可.
【详解】
(1)组成大正方形的小正方形数量可能是1、4、9、16、25、36…
而3+4+5+6+7+8=33在25和36之间,
所以组成大正方形的小正方形数量25个,多余8个.
故答案为:25,F.
(2)如图所示.
【点睛】
本题考查了利用旋转变换作图,正方体的性质,熟记正方形的性质是解题的关键.
32.9;900
【分析】
设遗产总数为克朗,根据题意可表示出第一个和第二个儿子分别获得的遗产,然后根据每个儿子分得一样多列出一元一次方程,从而求出总的遗产数,由此可得第一个儿子获得的遗产,即可得到每个儿子获得的遗产,从而求出总人数即可.
【详解】
解:设遗产总数为克朗,则:
第一个儿子分得:;
第二个儿子分得:;
∵每一个儿子所得财产一样多,
∴,
解得:,
∴遗产共有8100克朗,
则第一个儿子分得:(克朗),
即:每个儿子分得900克朗,
儿子共有:(人),
∴这位父亲共有9个儿子,每个儿子分得900克朗.
【点睛】
本题考查一元一次方程的实际应用,理解题意,准确设出未知数,并建立方程求解是解题关键.
同课章节目录
