复习正比例和反比例(课件) 数学六年级下册人教版(共18张PPT)
文档属性
| 名称 | 复习正比例和反比例(课件) 数学六年级下册人教版(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 600.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 09:38:30 | ||
图片预览






文档简介
(共18张PPT)
复习正比例和反比例
温故而知新
复习目标
1、通过复习让学生进一步理解
和掌握正比例、反比例的意义,能正
确判断两个量是否成正比例或反比例。
2、让学生进一步理解、掌握比例
尺的意义,能够运用比例尺的知识解
决实际问题。
一、正比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
如果用x和y表示两种相关联的量,用k表示
它们 的比值,那么上面这种数量关系式可以表示
为
y
X
=k (一定) 。
二、反比例
两种相关联的量,一种量变化,另一种量也随着变化 ,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用 x·y=k (一定)来表示。
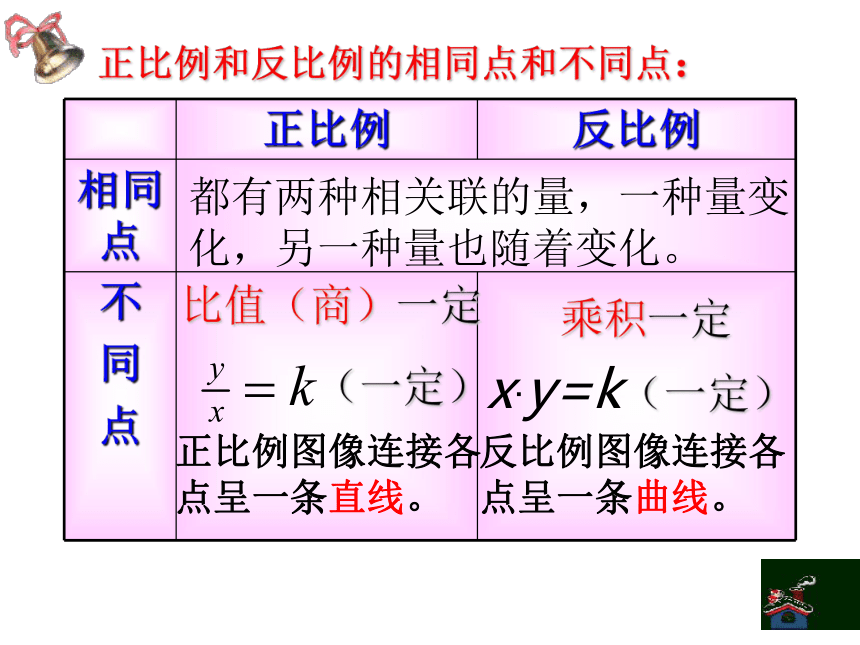
正比例 反比例
相同点
不
同
点
都有两种相关联的量,一种量变化,另一种量也随着变化。
x·y=k(一定)
乘积一定
比值(商)一定
(一定)
正比例和反比例的相同点和不同点:
正比例图像连接各
点呈一条直线。
反比例图像连接各
点呈一条曲线。
我会填:
2、⑴如果y=8x,x和y成( )比例。
⑵如果y= ,x和y成( )比例。
正
反
1、成正比例的两个量中相对应的两个数的( )
一定,成反比例的两个量中的相对应的两个数的
( )一定。
比值
乘积
判断下面每题中的两个量是否成比例?成什么比例?并说明理由。
(1)出油率一定,香油质量与芝麻的质量。( )
(2)一捆100米长的电线,用去的长度与剩下的长度。
( )
(3)一个数与它的倒数。 ( )
成正比例
成反比例
不成比例
香油质量÷芝麻的质量=出油率(一定)
a× =1 (a≠0)(一定)
1
a
用去的长度+剩下的长度=100米(一定)
(4)铺地面积一定,每块方砖面积和块数( )
成反比例
每块方砖面积 × 块数=铺地面积(一定)
图形的各边都按相同的比放大或缩小,图形才会像。放大或缩小后的图形大小不同,形状相同。
三、图形的放缩
按2:1画出下面图形放大后的图形.
1、在比例尺是1:400000的地图上,图上距离1厘米表示实际距离( )千米。也就是图上距离是实际距离的( ),实际距离是图上距离( )。
2、线段比例尺 0 50 100 150 200米,图上1厘米
线段表示实际距离( ),把它改写成数值比例尺
是( )。
4
400000
50米
1:5000
1、一个精密零件长3毫米,画在图上是12厘米,求这幅图的比例尺。
2、在一幅比例尺是1 :3000的地图上,岐岭大桥到校门的距离是8厘米,岐岭大桥到校门的实际距离是多少米?
3、我们班教室长8米、宽6米,画在比例尺为1 :200的平面图上,长和宽各应画多少厘米?
1、比例尺=( ),比例尺实际上是一个( )。
2、图上距离一定,实际距离和比例尺成( )比例。
3、五华到深圳的实际距离是300千米,平面图上的距离是6厘米,这幅地图的比例尺是
( )
图上距离:实际距离
比
反
1:5000000
一、填空题。
二、选择。
1.长方形的长一定,它的周长和宽( )。
A.成正比例 B. 成反比例 C. 不成比例
2.在一幅比例尺是1 :1000000的地图上,用( )表示
60千米。
A.0.6厘米 B. 6厘米 C. 60厘米
3.一幅图纸的比例尺是30:1,表示图上距离是实际距离的( )
A.30倍 B. 31倍 C.
C
B
A
三、判断。(对的打“√”,错的打“×”)
2、图上距离4厘米,表示实际距离200千米,
这幅地图的比例尺是1:5000000。( )
3、线段比例尺 和数值比例尺
1:20 表示的意义相同。( )
√
×
0
20
40千米
1、两种相关联的量,不成正比例就成反比例。 ( )
×
4、一个人的年龄和身高成正比例。( )
×
1、在一幅1:8000000的地图上,量得两
个城市间的距离是cm.如果飞机平均每时飞
行720km,这两个城市间大约要飞行多少时?
四、解决问题。
2、小明的身高是1.2m,它的影长
是2m.他在同一时间、同一地点测得一棵
树的影长是4.8m,那么这棵树有多高?
通过本节课的复习,你有
什么收获?
谢谢
复习正比例和反比例
温故而知新
复习目标
1、通过复习让学生进一步理解
和掌握正比例、反比例的意义,能正
确判断两个量是否成正比例或反比例。
2、让学生进一步理解、掌握比例
尺的意义,能够运用比例尺的知识解
决实际问题。
一、正比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
如果用x和y表示两种相关联的量,用k表示
它们 的比值,那么上面这种数量关系式可以表示
为
y
X
=k (一定) 。
二、反比例
两种相关联的量,一种量变化,另一种量也随着变化 ,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用 x·y=k (一定)来表示。
正比例 反比例
相同点
不
同
点
都有两种相关联的量,一种量变化,另一种量也随着变化。
x·y=k(一定)
乘积一定
比值(商)一定
(一定)
正比例和反比例的相同点和不同点:
正比例图像连接各
点呈一条直线。
反比例图像连接各
点呈一条曲线。
我会填:
2、⑴如果y=8x,x和y成( )比例。
⑵如果y= ,x和y成( )比例。
正
反
1、成正比例的两个量中相对应的两个数的( )
一定,成反比例的两个量中的相对应的两个数的
( )一定。
比值
乘积
判断下面每题中的两个量是否成比例?成什么比例?并说明理由。
(1)出油率一定,香油质量与芝麻的质量。( )
(2)一捆100米长的电线,用去的长度与剩下的长度。
( )
(3)一个数与它的倒数。 ( )
成正比例
成反比例
不成比例
香油质量÷芝麻的质量=出油率(一定)
a× =1 (a≠0)(一定)
1
a
用去的长度+剩下的长度=100米(一定)
(4)铺地面积一定,每块方砖面积和块数( )
成反比例
每块方砖面积 × 块数=铺地面积(一定)
图形的各边都按相同的比放大或缩小,图形才会像。放大或缩小后的图形大小不同,形状相同。
三、图形的放缩
按2:1画出下面图形放大后的图形.
1、在比例尺是1:400000的地图上,图上距离1厘米表示实际距离( )千米。也就是图上距离是实际距离的( ),实际距离是图上距离( )。
2、线段比例尺 0 50 100 150 200米,图上1厘米
线段表示实际距离( ),把它改写成数值比例尺
是( )。
4
400000
50米
1:5000
1、一个精密零件长3毫米,画在图上是12厘米,求这幅图的比例尺。
2、在一幅比例尺是1 :3000的地图上,岐岭大桥到校门的距离是8厘米,岐岭大桥到校门的实际距离是多少米?
3、我们班教室长8米、宽6米,画在比例尺为1 :200的平面图上,长和宽各应画多少厘米?
1、比例尺=( ),比例尺实际上是一个( )。
2、图上距离一定,实际距离和比例尺成( )比例。
3、五华到深圳的实际距离是300千米,平面图上的距离是6厘米,这幅地图的比例尺是
( )
图上距离:实际距离
比
反
1:5000000
一、填空题。
二、选择。
1.长方形的长一定,它的周长和宽( )。
A.成正比例 B. 成反比例 C. 不成比例
2.在一幅比例尺是1 :1000000的地图上,用( )表示
60千米。
A.0.6厘米 B. 6厘米 C. 60厘米
3.一幅图纸的比例尺是30:1,表示图上距离是实际距离的( )
A.30倍 B. 31倍 C.
C
B
A
三、判断。(对的打“√”,错的打“×”)
2、图上距离4厘米,表示实际距离200千米,
这幅地图的比例尺是1:5000000。( )
3、线段比例尺 和数值比例尺
1:20 表示的意义相同。( )
√
×
0
20
40千米
1、两种相关联的量,不成正比例就成反比例。 ( )
×
4、一个人的年龄和身高成正比例。( )
×
1、在一幅1:8000000的地图上,量得两
个城市间的距离是cm.如果飞机平均每时飞
行720km,这两个城市间大约要飞行多少时?
四、解决问题。
2、小明的身高是1.2m,它的影长
是2m.他在同一时间、同一地点测得一棵
树的影长是4.8m,那么这棵树有多高?
通过本节课的复习,你有
什么收获?
谢谢
