冀教版九年级数学下册 31.3 第1课时 频率的稳定性(共19张)
文档属性
| 名称 | 冀教版九年级数学下册 31.3 第1课时 频率的稳定性(共19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 865.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 20:59:10 | ||
图片预览






文档简介
(共19张PPT)
31.3 用频率估计概率
第三十一章 随机事件的概率
课时导入
欣赏著名球星詹姆斯图片,你知道詹姆斯罚球命中率是多少吗
当试验的所有结果不是
有限个,或各种可能结
果发生的可能性不相等
时,又该如何求事件发
生的概率呢
知识点
频率的稳定性
知1-讲
感悟新知
1
对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同. 当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近. 这个性质叫做频率的稳定性.
知1-练
感悟新知
例 1
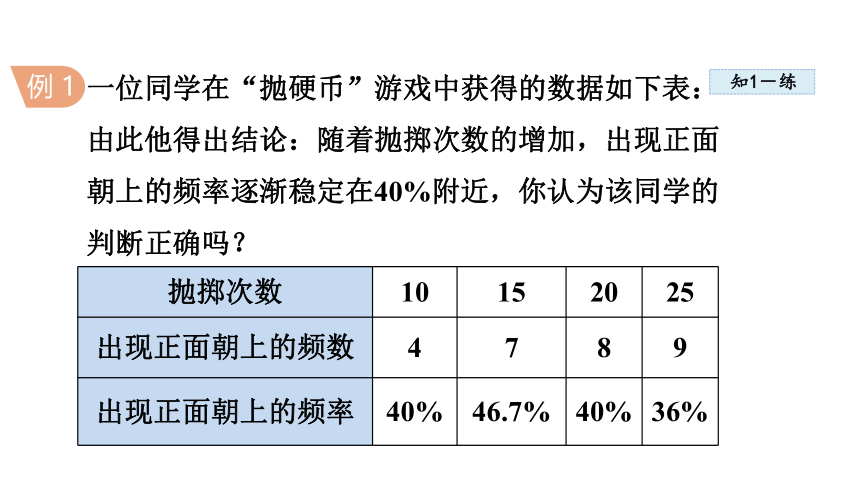
一位同学在“抛硬币”游戏中获得的数据如下表:
由此他得出结论:随着抛掷次数的增加,出现正面朝上的频率逐渐稳定在40%附近,你认为该同学的判断正确吗?
抛掷次数 10 15 20 25
出现正面朝上的频数 4 7 8 9
出现正面朝上的频率 40% 46.7% 40% 36%
知1-练
感悟新知
符号“ ”读作“等价于”,
它表示从符“ ”的左
端可以推出右端,从右
端也可以推出左端.
本题中的试验次数较少,应该多做一些试验,待事件出现的频率逐渐稳定到某一个数值,我们就可以用平稳时的频率去估计这一事件在每次抛掷时发生的可能性的大小.
导引:
该同学的判断不正确.
解:
知1-讲
总 结
感悟新知
频率的稳定性的前提是在试验次数足够多的情况下,对不同次数的试验,事件的频率可能不同.当试验次数较少时,看不出什么规律,但当试验次数足够多时,频率逐渐稳定到某一个数值.
知1-练
感悟新知
1.
关于掷一枚质地均匀硬币的试验,下列说法是否正确?为什么?
“正面朝上”和“反面朝上”的概率都是0.5,
所以掷100次硬币一定是“正面朝上”和“反
面朝上”各发生50次.
结果是“正面朝上”还是“反面朝上”,全凭
运气,没有什么规律.
知1-练
感悟新知
(1)不正确.因为虽然掷一枚硬币,出现正面朝上
和反面朝上的概率均为0.5,但出现“正面朝上”还
是“反面朝上”是随机事件;不能说掷100次硬币,
一定是“正面朝上”和“反面朝上”各出现50次.
(2)不正确.因为随着抛掷次数的增加,出现“正面朝
上”和“反面朝上”的频率逐渐稳定在0.5 附近.
解:
知1-练
感悟新知
2.
在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”,“2”,“3”,“4”,“5”,“6”,随着试验的次数增多,出现数字“1”的频率的变化趋势是__________________.
逐渐稳定到 附近
知1-练
感悟新知
3.
某人在做掷硬币试验时,投掷m次,正面朝上有n次(即正面朝上的频率p= ),则下列说法正确的是( )
A.p一定等于
B.p一定不等于
C.多投掷一次,p更接近
D.随着投掷次数的逐渐增加,p稳定在 附近
D
知1-练
感悟新知
4.
某种彩票的中奖机会是1%,下列说法正确的是( )
A.买1张这种彩票一定不会中奖
B.买1张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定
在1%附近
D
知1-练
感悟新知
5.
下列说法正确的是( )
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但每个人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后骰子上每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”“两个反面”“一正一反”的机会相同.
A.①② B.①③ C.②③ D.③④
C
知识点
频率稳定性的应用
知2-讲
感悟新知
2
下表是某批足球质量检验获得的数据,请根据此表回答,当抽取的足球数很大时,这批足球优等品的频率会在常数_________附近摆动.
抽取的足球数 50 100 200 500 1000 2000
优等品数 47 95 194 472 953 1902
0.95
例2
随机事件
知2-讲
感悟新知
频数=
≈0.95.
即这批足球优等品的频率会在常数0.95附近摆动.
解析:
随机事件
知2-练
感悟新知
1.
为了看图钉落地后钉尖着地的频率有多大,小明做
了大量重复试验,发现钉尖着地的次数是试验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着试验次数的增加,钉尖着地的频率逐渐稳定
在某一个常数附近
C.前10次试验结束后,钉尖着地的次数一定是4次
D.前10次试验结束后,钉尖着地的次数不一定是4次
C
随机事件
知2-练
感悟新知
2.
某小组做实验时,统计了某一结果出现的频率,绘制了如图
所示的折线统计图,则符合这一结果的实验最有可能是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张 牌,其
花色是红桃
C.暗箱中有1个红球和2个黄球,
它们只有颜色上的区别,
从中任取一球是黄球
D.掷一枚质地均匀的正六面体
骰子,向上的面的点数是4
D
随机事件
知2-练
感悟新知
3.
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A.13个 B.15个
C.16个 D.12个
D
知2-练
感悟新知
4.
在一个不透明的袋子中装有除颜色外其余均相同的n个
小球,其中5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:根据列表,可以估计出n的值是________.
10
摸球试验次数 100 1 000 5 000 10 000 50 000 100 000
摸出黑球次数 46 487 2 506 5 008 24 996 50 007
课堂小结
频率的稳定性
当试验次数较少时,频率是不稳定的,波动较大,因为随机事件的发生具有偶然性,几次试验中,该事件可能发生,也可能不发生.只有通过大量的试验,频率才呈逐渐稳定的趋势,也就是说试验次数越多,频率就越稳定,这个性质叫做频率的稳定性.
31.3 用频率估计概率
第三十一章 随机事件的概率
课时导入
欣赏著名球星詹姆斯图片,你知道詹姆斯罚球命中率是多少吗
当试验的所有结果不是
有限个,或各种可能结
果发生的可能性不相等
时,又该如何求事件发
生的概率呢
知识点
频率的稳定性
知1-讲
感悟新知
1
对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同. 当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近. 这个性质叫做频率的稳定性.
知1-练
感悟新知
例 1
一位同学在“抛硬币”游戏中获得的数据如下表:
由此他得出结论:随着抛掷次数的增加,出现正面朝上的频率逐渐稳定在40%附近,你认为该同学的判断正确吗?
抛掷次数 10 15 20 25
出现正面朝上的频数 4 7 8 9
出现正面朝上的频率 40% 46.7% 40% 36%
知1-练
感悟新知
符号“ ”读作“等价于”,
它表示从符“ ”的左
端可以推出右端,从右
端也可以推出左端.
本题中的试验次数较少,应该多做一些试验,待事件出现的频率逐渐稳定到某一个数值,我们就可以用平稳时的频率去估计这一事件在每次抛掷时发生的可能性的大小.
导引:
该同学的判断不正确.
解:
知1-讲
总 结
感悟新知
频率的稳定性的前提是在试验次数足够多的情况下,对不同次数的试验,事件的频率可能不同.当试验次数较少时,看不出什么规律,但当试验次数足够多时,频率逐渐稳定到某一个数值.
知1-练
感悟新知
1.
关于掷一枚质地均匀硬币的试验,下列说法是否正确?为什么?
“正面朝上”和“反面朝上”的概率都是0.5,
所以掷100次硬币一定是“正面朝上”和“反
面朝上”各发生50次.
结果是“正面朝上”还是“反面朝上”,全凭
运气,没有什么规律.
知1-练
感悟新知
(1)不正确.因为虽然掷一枚硬币,出现正面朝上
和反面朝上的概率均为0.5,但出现“正面朝上”还
是“反面朝上”是随机事件;不能说掷100次硬币,
一定是“正面朝上”和“反面朝上”各出现50次.
(2)不正确.因为随着抛掷次数的增加,出现“正面朝
上”和“反面朝上”的频率逐渐稳定在0.5 附近.
解:
知1-练
感悟新知
2.
在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”,“2”,“3”,“4”,“5”,“6”,随着试验的次数增多,出现数字“1”的频率的变化趋势是__________________.
逐渐稳定到 附近
知1-练
感悟新知
3.
某人在做掷硬币试验时,投掷m次,正面朝上有n次(即正面朝上的频率p= ),则下列说法正确的是( )
A.p一定等于
B.p一定不等于
C.多投掷一次,p更接近
D.随着投掷次数的逐渐增加,p稳定在 附近
D
知1-练
感悟新知
4.
某种彩票的中奖机会是1%,下列说法正确的是( )
A.买1张这种彩票一定不会中奖
B.买1张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定
在1%附近
D
知1-练
感悟新知
5.
下列说法正确的是( )
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但每个人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后骰子上每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”“两个反面”“一正一反”的机会相同.
A.①② B.①③ C.②③ D.③④
C
知识点
频率稳定性的应用
知2-讲
感悟新知
2
下表是某批足球质量检验获得的数据,请根据此表回答,当抽取的足球数很大时,这批足球优等品的频率会在常数_________附近摆动.
抽取的足球数 50 100 200 500 1000 2000
优等品数 47 95 194 472 953 1902
0.95
例2
随机事件
知2-讲
感悟新知
频数=
≈0.95.
即这批足球优等品的频率会在常数0.95附近摆动.
解析:
随机事件
知2-练
感悟新知
1.
为了看图钉落地后钉尖着地的频率有多大,小明做
了大量重复试验,发现钉尖着地的次数是试验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着试验次数的增加,钉尖着地的频率逐渐稳定
在某一个常数附近
C.前10次试验结束后,钉尖着地的次数一定是4次
D.前10次试验结束后,钉尖着地的次数不一定是4次
C
随机事件
知2-练
感悟新知
2.
某小组做实验时,统计了某一结果出现的频率,绘制了如图
所示的折线统计图,则符合这一结果的实验最有可能是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张 牌,其
花色是红桃
C.暗箱中有1个红球和2个黄球,
它们只有颜色上的区别,
从中任取一球是黄球
D.掷一枚质地均匀的正六面体
骰子,向上的面的点数是4
D
随机事件
知2-练
感悟新知
3.
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A.13个 B.15个
C.16个 D.12个
D
知2-练
感悟新知
4.
在一个不透明的袋子中装有除颜色外其余均相同的n个
小球,其中5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:根据列表,可以估计出n的值是________.
10
摸球试验次数 100 1 000 5 000 10 000 50 000 100 000
摸出黑球次数 46 487 2 506 5 008 24 996 50 007
课堂小结
频率的稳定性
当试验次数较少时,频率是不稳定的,波动较大,因为随机事件的发生具有偶然性,几次试验中,该事件可能发生,也可能不发生.只有通过大量的试验,频率才呈逐渐稳定的趋势,也就是说试验次数越多,频率就越稳定,这个性质叫做频率的稳定性.
