冀教版九年级数学下册 31.4 第1课时 用列举法求概率(共30张)
文档属性
| 名称 | 冀教版九年级数学下册 31.4 第1课时 用列举法求概率(共30张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
31.4 用列举法求简单事件的概率
第三十一章 随机事件的概率
课时导入
回顾与思考
在一次试验中,如果可能出现的结果只有有限
个,且各种结果出现的可能性大小相等,那么我们
可以通过列举试验结果的方法,求出随机事件发生
的概率.
知识点
用列举法求概率(等可能事件结果个数较少)
知1-讲
感悟新知
1
用列举法求某一事件的概率,关键是找出所有可
能发生的结果以及某一事件发生的结果.
知1-练
感悟新知
例 1
如图,四个开关按钮中有两个各控制一盏灯,另两个按钮控制一个发音装置. 当连续按对两个按钮点亮两盏灯时,“闯关 成功”;而只要按错一个按钮,就会发出 “闯关失败”的声音. 求“闯关成功”的 概率.
知1-练
感悟新知
符号“ ”读作“等价于”,
它表示从符“ ”的左
端可以推出右端,从右
端也可以推出左端.
不妨设1号,2号按钮各控制一盏灯,连续按两个
按钮(不考虑按钮的顺序)的所有可能结果列表如下:
解:
按钮代号 12 13 14 23 24 34
结果 成功 失败 失败 失败 失败 失败
所有可能结果有6种,它们都是等可能发生的,而其中只有一种结 果为“闯关成功”,
所以,P(闯关成功)=
知1-讲
总 结
感悟新知
直接列举法求概率的采用:当试验的结果是有限个的,且这些结果出现的可能性相等,并决定这些概率的因素只有一个时采用.
知1-练
感悟新知
甲、乙、丙三人站成一排拍照,则甲站在中间的概率是( )
A. B.
C. D.
1.
B
知1-练
感悟新知
有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,随机抽取3张,用抽到的三个数字作为边长,恰能构成三角形的概率是( )
A. B.
C. D.
2.
A
知1-练
感悟新知
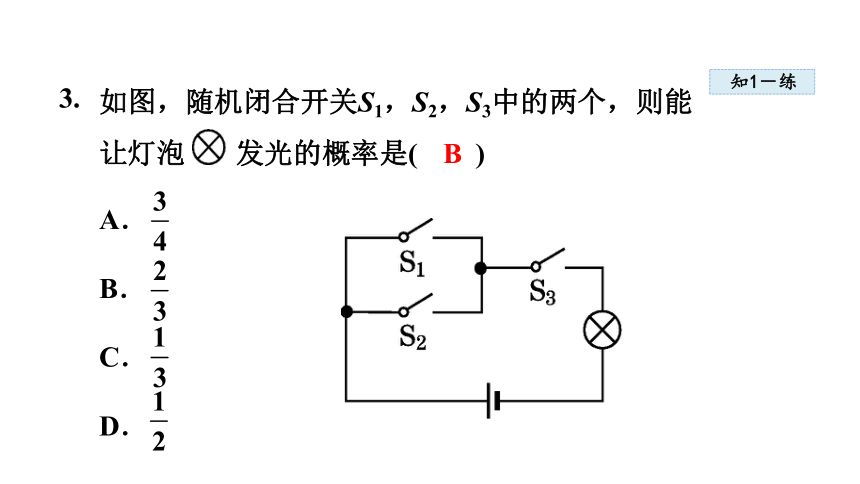
如图,随机闭合开关S1,S2,S3中的两个,则能让灯泡 发光的概率是( )
A.
B.
C.
D.
3.
B
知识点
用列表法求概率(等可能事件结果个数较多)
知2-讲
感悟新知
2
对于求两步以上的概率采用列表法.
随机事件
知2-练
感悟新知
例2
同时掷两枚质地均匀的骰子,计算下列事件
的概率:(1)两枚骰子的点数相同; (2)两枚骰子点数的和是9; (3)至少有一枚骰子的点数为2.
分析:当一次试验是掷两枚骰子时,为不重不漏地列
出所有可能的结果,通常采用列表法.
随机事件
知2-练
感悟新知
解:两枚骰子分别记为第1枚和第2枚,可以用下表列
举出所有可能出现的结果.
随机事件
知2-练
感悟新知
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
第1枚
第2枚
随机事件
知2-练
感悟新知
(1)两枚骰子的点数相同(记为事件A)的结果有6种,
即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),
所以
由上表可以看出,同时掷两枚骰子,可能出现的结果
有36种,并且它们出现的可能性相同.
(2)两枚骰子的点数和是9(记为事件B)的结果有4种,
即(3,6),(4,5),(5,4),(6,3),所以
随机事件
知2-练
感悟新知
(3)至少有一枚骰子的点数为2(记为事件C)的结果
有11种,即(1,2),(2,1),(2,2),(2,3),(2,4),
(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),
所以
知2-讲
总 结
感悟新知
2.适用条件:如果事件中各种结果出现的可能性均等,
含有两次操作(如掷骰子两次)或两个条件(如两个转盘)
的事件.
1.用列表法求概率的步骤:①列表;②通过表格计数,
确定所有等可能的结果数n和关注的结果数m的值;
③利用概率公式 计算出事件的概率.
知2-讲
感悟新知
特别提醒:
1. 列表法适用于求两步试验的概率,不适用于求三步及三步以上试验的概率.
2.列表法适用的条件还可以理解为各种结果出现的可能性相等,
含有两次操作(如掷一枚骰子两次)或两个条件(如两个转盘)
的事件.
随机事件
知2-练
感悟新知
对本节“一起探究”投掷正四面体的试验,求下列事件的概率.
A=“两数之和为偶数 ”.
B=“两数之和为奇数”.
C=“两数之和大于5”.
D=“两数之和为3的倍数”.
1.
知2-练
感悟新知
在投掷四面体的试验中,投掷两次,有4×4=16(个)等可能的结果,用表格表示对应的两个数的和.
解:
+ 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
知2-练
感悟新知
从表中可以看出事件A包含8个等可能的结果,事件B包含8个等可能的结果;事件C包含6个等可能的结果,事件D包含5个等可能的结果,所以P(A)=
P(B)= P(C)= P(D)=
知2-练
感悟新知
从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y= 的图像上的概率是( )
A. B.
C. D.
2.
D
知2-练
感悟新知
小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B.
C. D.
3.
A
知2-练
感悟新知
小强和小华两人玩“石头、剪刀、布”游戏,随机出手一次,则两人平局的概率为( )
A. B.
C. D.
4.
B
知2-练
感悟新知
若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上的数字为7,则从3,4,5,6,8,9中任选两数,与7组成“中高数”的概率是( )
A. B.
C. D.
5.
C
知2-练
感悟新知
学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转
盘,每个转盘均被分成完全相同的四个区域,分别用数字“1”“2”“3”“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若有指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是( )
A. B.
C. D.
6.
C
知2-练
感悟新知
有6张看上去无差别的卡片,上面分别写着1,2,3,4,5,6,随机抽取一张后,放回并混在一起,再随机抽取一张,两次抽取的数字的积为奇数的概率是( )
A. B.
C. D.
7.
B
课堂小结
用列举法求概率
1.列举法求概率的前提:
(1)一次试验中,可能出现的结果是有限个;
(2)一次试验中,各种结果发生的可能性相等.
2.列表法一般应用于两个元素且结果的可能性
较多的题目中.
课堂小结
用列举法求概率
某电视栏目中的百宝箱互动环节是一种竞猜游戏,游戏规则如下:在20张商标牌中,有5张商标牌的背面注明一定金额,其余商标牌的背面均是一张哭脸,若翻到哭脸就不得奖;反之,则得奖.参与游戏的观众有三次翻牌的机会(翻过的牌不能再翻),某人前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( )
A. B. C. D.
C
课堂小结
用列举法求概率
诊断:20张商标牌中有奖的有5张,该参与者前两次翻牌均
获奖,而翻过的牌不能再翻,因此剩下的18张商标牌
中,有奖的商标牌有3张,故他第三次翻牌获奖的概
率是 = ,而不是 .
课堂小结
用列举法求概率
易错点:不能准确区分放回抽样与不放回抽样对事件发
生的概率的影响.
31.4 用列举法求简单事件的概率
第三十一章 随机事件的概率
课时导入
回顾与思考
在一次试验中,如果可能出现的结果只有有限
个,且各种结果出现的可能性大小相等,那么我们
可以通过列举试验结果的方法,求出随机事件发生
的概率.
知识点
用列举法求概率(等可能事件结果个数较少)
知1-讲
感悟新知
1
用列举法求某一事件的概率,关键是找出所有可
能发生的结果以及某一事件发生的结果.
知1-练
感悟新知
例 1
如图,四个开关按钮中有两个各控制一盏灯,另两个按钮控制一个发音装置. 当连续按对两个按钮点亮两盏灯时,“闯关 成功”;而只要按错一个按钮,就会发出 “闯关失败”的声音. 求“闯关成功”的 概率.
知1-练
感悟新知
符号“ ”读作“等价于”,
它表示从符“ ”的左
端可以推出右端,从右
端也可以推出左端.
不妨设1号,2号按钮各控制一盏灯,连续按两个
按钮(不考虑按钮的顺序)的所有可能结果列表如下:
解:
按钮代号 12 13 14 23 24 34
结果 成功 失败 失败 失败 失败 失败
所有可能结果有6种,它们都是等可能发生的,而其中只有一种结 果为“闯关成功”,
所以,P(闯关成功)=
知1-讲
总 结
感悟新知
直接列举法求概率的采用:当试验的结果是有限个的,且这些结果出现的可能性相等,并决定这些概率的因素只有一个时采用.
知1-练
感悟新知
甲、乙、丙三人站成一排拍照,则甲站在中间的概率是( )
A. B.
C. D.
1.
B
知1-练
感悟新知
有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,随机抽取3张,用抽到的三个数字作为边长,恰能构成三角形的概率是( )
A. B.
C. D.
2.
A
知1-练
感悟新知
如图,随机闭合开关S1,S2,S3中的两个,则能让灯泡 发光的概率是( )
A.
B.
C.
D.
3.
B
知识点
用列表法求概率(等可能事件结果个数较多)
知2-讲
感悟新知
2
对于求两步以上的概率采用列表法.
随机事件
知2-练
感悟新知
例2
同时掷两枚质地均匀的骰子,计算下列事件
的概率:(1)两枚骰子的点数相同; (2)两枚骰子点数的和是9; (3)至少有一枚骰子的点数为2.
分析:当一次试验是掷两枚骰子时,为不重不漏地列
出所有可能的结果,通常采用列表法.
随机事件
知2-练
感悟新知
解:两枚骰子分别记为第1枚和第2枚,可以用下表列
举出所有可能出现的结果.
随机事件
知2-练
感悟新知
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
第1枚
第2枚
随机事件
知2-练
感悟新知
(1)两枚骰子的点数相同(记为事件A)的结果有6种,
即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),
所以
由上表可以看出,同时掷两枚骰子,可能出现的结果
有36种,并且它们出现的可能性相同.
(2)两枚骰子的点数和是9(记为事件B)的结果有4种,
即(3,6),(4,5),(5,4),(6,3),所以
随机事件
知2-练
感悟新知
(3)至少有一枚骰子的点数为2(记为事件C)的结果
有11种,即(1,2),(2,1),(2,2),(2,3),(2,4),
(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),
所以
知2-讲
总 结
感悟新知
2.适用条件:如果事件中各种结果出现的可能性均等,
含有两次操作(如掷骰子两次)或两个条件(如两个转盘)
的事件.
1.用列表法求概率的步骤:①列表;②通过表格计数,
确定所有等可能的结果数n和关注的结果数m的值;
③利用概率公式 计算出事件的概率.
知2-讲
感悟新知
特别提醒:
1. 列表法适用于求两步试验的概率,不适用于求三步及三步以上试验的概率.
2.列表法适用的条件还可以理解为各种结果出现的可能性相等,
含有两次操作(如掷一枚骰子两次)或两个条件(如两个转盘)
的事件.
随机事件
知2-练
感悟新知
对本节“一起探究”投掷正四面体的试验,求下列事件的概率.
A=“两数之和为偶数 ”.
B=“两数之和为奇数”.
C=“两数之和大于5”.
D=“两数之和为3的倍数”.
1.
知2-练
感悟新知
在投掷四面体的试验中,投掷两次,有4×4=16(个)等可能的结果,用表格表示对应的两个数的和.
解:
+ 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
知2-练
感悟新知
从表中可以看出事件A包含8个等可能的结果,事件B包含8个等可能的结果;事件C包含6个等可能的结果,事件D包含5个等可能的结果,所以P(A)=
P(B)= P(C)= P(D)=
知2-练
感悟新知
从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y= 的图像上的概率是( )
A. B.
C. D.
2.
D
知2-练
感悟新知
小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B.
C. D.
3.
A
知2-练
感悟新知
小强和小华两人玩“石头、剪刀、布”游戏,随机出手一次,则两人平局的概率为( )
A. B.
C. D.
4.
B
知2-练
感悟新知
若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上的数字为7,则从3,4,5,6,8,9中任选两数,与7组成“中高数”的概率是( )
A. B.
C. D.
5.
C
知2-练
感悟新知
学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转
盘,每个转盘均被分成完全相同的四个区域,分别用数字“1”“2”“3”“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若有指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是( )
A. B.
C. D.
6.
C
知2-练
感悟新知
有6张看上去无差别的卡片,上面分别写着1,2,3,4,5,6,随机抽取一张后,放回并混在一起,再随机抽取一张,两次抽取的数字的积为奇数的概率是( )
A. B.
C. D.
7.
B
课堂小结
用列举法求概率
1.列举法求概率的前提:
(1)一次试验中,可能出现的结果是有限个;
(2)一次试验中,各种结果发生的可能性相等.
2.列表法一般应用于两个元素且结果的可能性
较多的题目中.
课堂小结
用列举法求概率
某电视栏目中的百宝箱互动环节是一种竞猜游戏,游戏规则如下:在20张商标牌中,有5张商标牌的背面注明一定金额,其余商标牌的背面均是一张哭脸,若翻到哭脸就不得奖;反之,则得奖.参与游戏的观众有三次翻牌的机会(翻过的牌不能再翻),某人前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( )
A. B. C. D.
C
课堂小结
用列举法求概率
诊断:20张商标牌中有奖的有5张,该参与者前两次翻牌均
获奖,而翻过的牌不能再翻,因此剩下的18张商标牌
中,有奖的商标牌有3张,故他第三次翻牌获奖的概
率是 = ,而不是 .
课堂小结
用列举法求概率
易错点:不能准确区分放回抽样与不放回抽样对事件发
生的概率的影响.
