华东师大版八年级上册11.1.2立方根课件(27张ppt)
文档属性
| 名称 | 华东师大版八年级上册11.1.2立方根课件(27张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 06:24:02 | ||
图片预览








文档简介
(共27张PPT)
(——成功在于坚持,这是一个并不神秘的秘诀。)
开学第一天,大哲学家苏格拉底对学生们说:“今天,我们只做一件最简单也是最容易做的事儿:每个人把胳膊尽量都往前甩,然后再尽量往后甩。”说着,苏格拉底示范了一遍,“从今天开始,每天做300下,大家能做到吗?” 学生们都笑了,这么简单的事情,有什么做不到的? 过了一个月,苏格拉底问学生们:“每天甩手300下,哪些同学坚持了?”有90%的同学骄傲地举起了手。又过了一个月,苏格拉底再问,这回,坚持下来的同学只剩下了八成。 一年过后,苏格拉底再一次问大家:“请大家告诉我,最简单的甩手运动,还有哪几位同学坚持了?”这时候,整个教室里,只有一个人举起了手。这个学生就是后来成为古希腊另一位大哲学家的柏拉图。
11.1.2 立方根
知道立方根的概念及性质,会用根号表示一个数的立方根。
会用开立方运算求一个数的立方根,知道立方与开立方是互逆运算。
会用计算器求一个数的立方根。
立方根的概念与性质及求法
16的平方根是______
-16的平方根是________
0的平方根是________
没有平方根
0
一个正数有正负两个平方根,它们互为相反数;
零的平方根是零,
负数没有平方根.
旧知回顾
23=8 33=27 43=64
53=125 63=216 73=343
83=512 93=729 103=1000
113=1331 123=1728
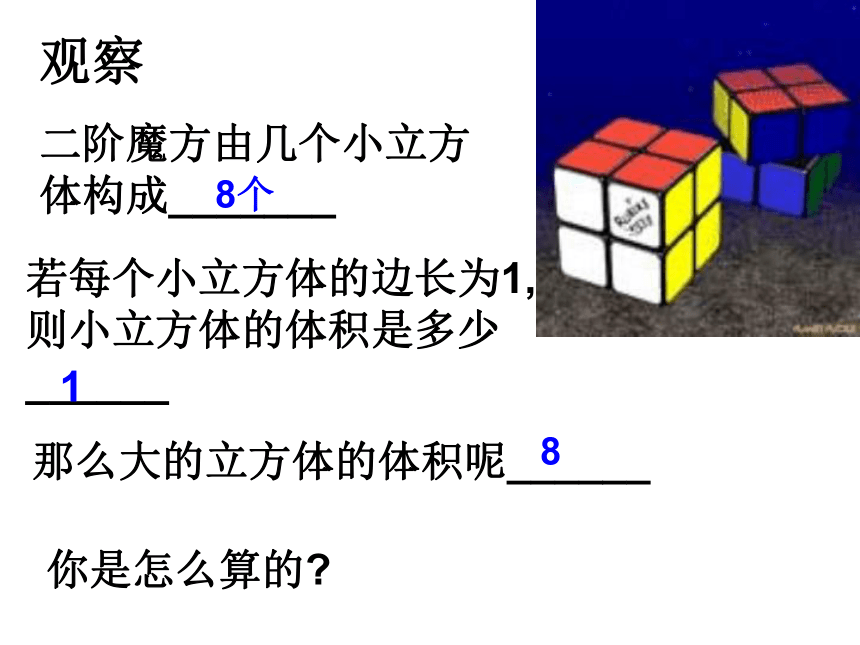
观察
二阶魔方由几个小立方体构成_______
若每个小立方体的边长为1,则小立方体的体积是多少______
你是怎么算的
8个
1
8
那么大的立方体的体积呢______
要做一个容积为 27 的正方体形状的包装箱, 这种包装箱的边长应该是多少
解:设这种包装箱的边长为x m,则:
=27
∵ =27
∴ =3
即这种包装箱的边长为3 m。
要做一个容积为 27 的正方体形状的包装箱, 这种包装箱的边长应该是多少
什么数的立方等于-27
想一想
因为3的立方等于27,那么3就叫做27的立方根.
因为-3的立方等于-27,那么-3就叫做-27的立方根.
=-27
试一试:
你能给数的立方根下个定义吗?
一般地,如果一个数的立方等于a,那
么这个数叫做a的立方根或(三次方根).
即:如果 =a,那么x叫做a的立方根.记作:
求一个数的立方根的运算,叫做开立方.开立方与立方是互逆运算。
被开方数
立方根
根指数
注意:根指数是3 时,绝对不能省略不写。
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
到现在我们学了几种运算
+,-,x,÷,乘方,开平方,开立方
,
,
,
你会区别下列的数吗?
表示a的算术平方根
表示a的平方根或a的二次方根
表示a的立方根或a的三次方根
表示a的四次方根
正数有立方根吗?如果有,有几个。
负数呢?
零呢?
从上面的例1可知:一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。
从上面的例题可知:
由此可得出:
也就是把根号里的“负号”直接从根号里面提到了根号“外面” 。
特别注意:平方根不能这样哟!
由此得出求一个负数的立方根的一般方法:
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
尝试练习:
根据立方根的意义填空:
1、因为 ,所以8的立方根是( )。
2、因为( )=0.125,所以0.125的立方根是( )。
3、因为( )=0,所以0的立方根是( )。
4、因为( )=-8,所以-8的立方根是( )。
5、因为( )= - ,所以- 的立方根是( )。
3
3
3
3
2
0.5
0
0
-2
-2
-
-
0.5
例1 求下列各数的立方根
(1) 27 (2)-27 (3) (4)-0.064 (5) 0
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)∵
∴ 的立方根是
3
1
3
(4) -0.064
∴-0.064的立方根是-0.4
解 ∵0 =0
3
∴0的立方根是0
解∵
(5) 0
由上面练习的结果看,正数有立方根吗?如果有,有几个 负数呢?0呢?这些立方根各有什么特点?
从上面的练习可知:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
探究练习:
1、 =______,- =______
____-
2、 =______, =______
____
-2
-2
=
-3
-3
=
例 求下列各式的值:
(1)
(2)
(3)
解: =4
解: =-5
解: =
平方根 立方根
定
义
性
质 正
数
0
负
数
开
方
表
示
如果一个数的平方等于a,那么
这个数就叫a的平方根。
如果一个数的立方等于a,那么
这个数就叫a的立方根。
有两个平方根,互为相反数
有一个平方根,是0
没有平方根
求一个数的平方根的运算叫开
平方;开平方与平方是互逆运算。
,其中a 是被开方数,
2是根指数(省略)
求一个数的立方根的运算叫开
立方;开立方与立方是互逆运算。
有一个立方根,也是负数
有一个立方根,是0
有一个立方根,也是正数
,其中a 是被开方数,
3是根指数(不能省略)
讨论:你能归纳出平方根和立方根的异同点吗
2.平方根与立方根的直观比较:
平方根 立方根
正数
0
负数
两个平方根,它们
互为相反数
一个正的立方根
0
0
没有
一个负的立方根
小 结
1、有哪个数没有立方根吗?
2、一个数 a 有几个立方根?
正数的立方根是正数
0的立方根是0
负数的立方根是负数
P7 习题12.1 第1题
第2题
(——成功在于坚持,这是一个并不神秘的秘诀。)
开学第一天,大哲学家苏格拉底对学生们说:“今天,我们只做一件最简单也是最容易做的事儿:每个人把胳膊尽量都往前甩,然后再尽量往后甩。”说着,苏格拉底示范了一遍,“从今天开始,每天做300下,大家能做到吗?” 学生们都笑了,这么简单的事情,有什么做不到的? 过了一个月,苏格拉底问学生们:“每天甩手300下,哪些同学坚持了?”有90%的同学骄傲地举起了手。又过了一个月,苏格拉底再问,这回,坚持下来的同学只剩下了八成。 一年过后,苏格拉底再一次问大家:“请大家告诉我,最简单的甩手运动,还有哪几位同学坚持了?”这时候,整个教室里,只有一个人举起了手。这个学生就是后来成为古希腊另一位大哲学家的柏拉图。
11.1.2 立方根
知道立方根的概念及性质,会用根号表示一个数的立方根。
会用开立方运算求一个数的立方根,知道立方与开立方是互逆运算。
会用计算器求一个数的立方根。
立方根的概念与性质及求法
16的平方根是______
-16的平方根是________
0的平方根是________
没有平方根
0
一个正数有正负两个平方根,它们互为相反数;
零的平方根是零,
负数没有平方根.
旧知回顾
23=8 33=27 43=64
53=125 63=216 73=343
83=512 93=729 103=1000
113=1331 123=1728
观察
二阶魔方由几个小立方体构成_______
若每个小立方体的边长为1,则小立方体的体积是多少______
你是怎么算的
8个
1
8
那么大的立方体的体积呢______
要做一个容积为 27 的正方体形状的包装箱, 这种包装箱的边长应该是多少
解:设这种包装箱的边长为x m,则:
=27
∵ =27
∴ =3
即这种包装箱的边长为3 m。
要做一个容积为 27 的正方体形状的包装箱, 这种包装箱的边长应该是多少
什么数的立方等于-27
想一想
因为3的立方等于27,那么3就叫做27的立方根.
因为-3的立方等于-27,那么-3就叫做-27的立方根.
=-27
试一试:
你能给数的立方根下个定义吗?
一般地,如果一个数的立方等于a,那
么这个数叫做a的立方根或(三次方根).
即:如果 =a,那么x叫做a的立方根.记作:
求一个数的立方根的运算,叫做开立方.开立方与立方是互逆运算。
被开方数
立方根
根指数
注意:根指数是3 时,绝对不能省略不写。
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
到现在我们学了几种运算
+,-,x,÷,乘方,开平方,开立方
,
,
,
你会区别下列的数吗?
表示a的算术平方根
表示a的平方根或a的二次方根
表示a的立方根或a的三次方根
表示a的四次方根
正数有立方根吗?如果有,有几个。
负数呢?
零呢?
从上面的例1可知:一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。
从上面的例题可知:
由此可得出:
也就是把根号里的“负号”直接从根号里面提到了根号“外面” 。
特别注意:平方根不能这样哟!
由此得出求一个负数的立方根的一般方法:
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
尝试练习:
根据立方根的意义填空:
1、因为 ,所以8的立方根是( )。
2、因为( )=0.125,所以0.125的立方根是( )。
3、因为( )=0,所以0的立方根是( )。
4、因为( )=-8,所以-8的立方根是( )。
5、因为( )= - ,所以- 的立方根是( )。
3
3
3
3
2
0.5
0
0
-2
-2
-
-
0.5
例1 求下列各数的立方根
(1) 27 (2)-27 (3) (4)-0.064 (5) 0
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)∵
∴ 的立方根是
3
1
3
(4) -0.064
∴-0.064的立方根是-0.4
解 ∵0 =0
3
∴0的立方根是0
解∵
(5) 0
由上面练习的结果看,正数有立方根吗?如果有,有几个 负数呢?0呢?这些立方根各有什么特点?
从上面的练习可知:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
探究练习:
1、 =______,- =______
____-
2、 =______, =______
____
-2
-2
=
-3
-3
=
例 求下列各式的值:
(1)
(2)
(3)
解: =4
解: =-5
解: =
平方根 立方根
定
义
性
质 正
数
0
负
数
开
方
表
示
如果一个数的平方等于a,那么
这个数就叫a的平方根。
如果一个数的立方等于a,那么
这个数就叫a的立方根。
有两个平方根,互为相反数
有一个平方根,是0
没有平方根
求一个数的平方根的运算叫开
平方;开平方与平方是互逆运算。
,其中a 是被开方数,
2是根指数(省略)
求一个数的立方根的运算叫开
立方;开立方与立方是互逆运算。
有一个立方根,也是负数
有一个立方根,是0
有一个立方根,也是正数
,其中a 是被开方数,
3是根指数(不能省略)
讨论:你能归纳出平方根和立方根的异同点吗
2.平方根与立方根的直观比较:
平方根 立方根
正数
0
负数
两个平方根,它们
互为相反数
一个正的立方根
0
0
没有
一个负的立方根
小 结
1、有哪个数没有立方根吗?
2、一个数 a 有几个立方根?
正数的立方根是正数
0的立方根是0
负数的立方根是负数
P7 习题12.1 第1题
第2题
