多边形的面积计算(课件) 数学五年级上册 人教版(共23张PPT)
文档属性
| 名称 | 多边形的面积计算(课件) 数学五年级上册 人教版(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 109.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览


文档简介
(共23张PPT)
多边形面积的计算
在数学课上我们已经掌握了几种基本图形的面积计算方法:
正方形的面积=
边长×边长
S=a2
长方形的面积=
长×宽
S=ab
平行四边形的面积=
底×高
S=ah
三角形的面积=
底×高÷2
S=ah÷2
梯形的面积=
(上底+下底)×高÷2
S=(a+b)h÷2
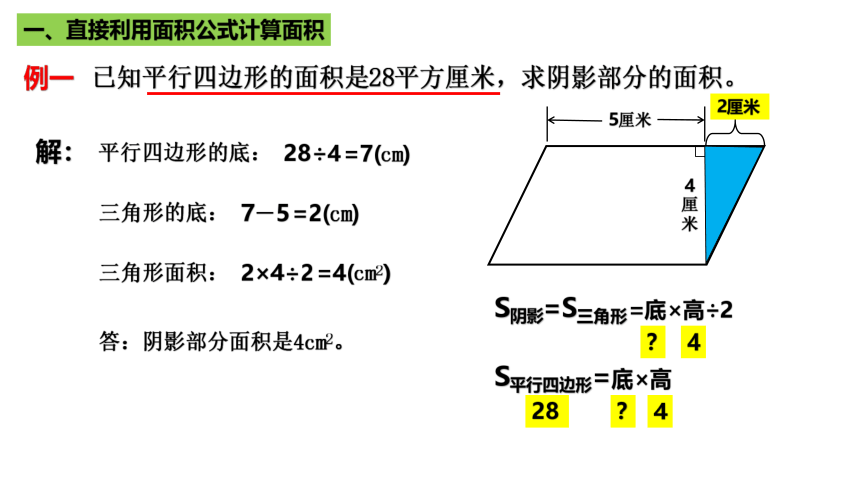
例一 已知平行四边形的面积是28平方厘米,求阴影部分的面积。
一、直接利用面积公式计算面积
5厘米
4厘米
S阴影=S三角形
=底×高÷2
底
?
4
S平行四边形=
底×高
28
?
4
解:
平行四边形的底:
28÷4
=7(cm)
三角形的底:
7-5
=2(cm)
三角形面积:
2×4÷2
=4(cm2)
2厘米
答:阴影部分面积是4cm2。
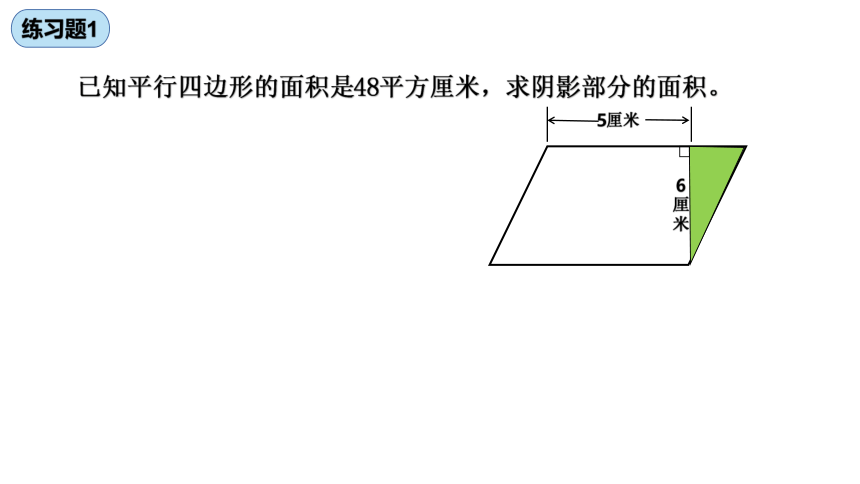
练习题1
已知平行四边形的面积是48平方厘米,求阴影部分的面积。
5厘米
6厘米
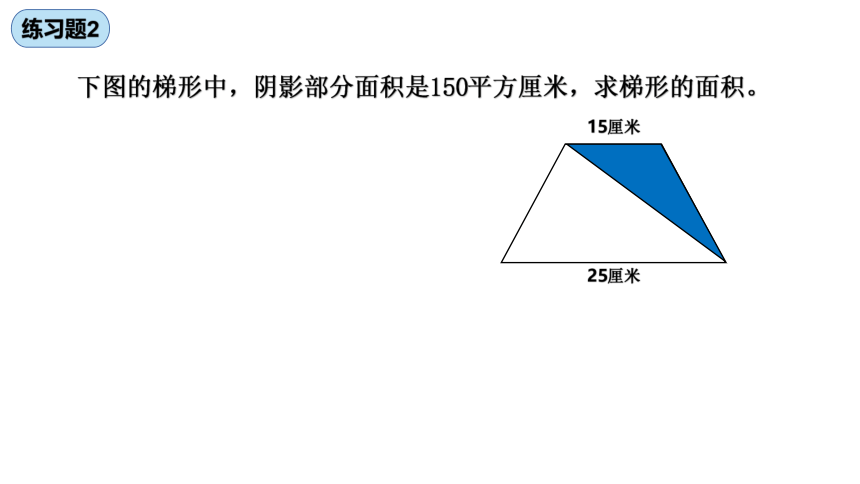
练习题2
下图的梯形中,阴影部分面积是150平方厘米,求梯形的面积。
15厘米
25厘米
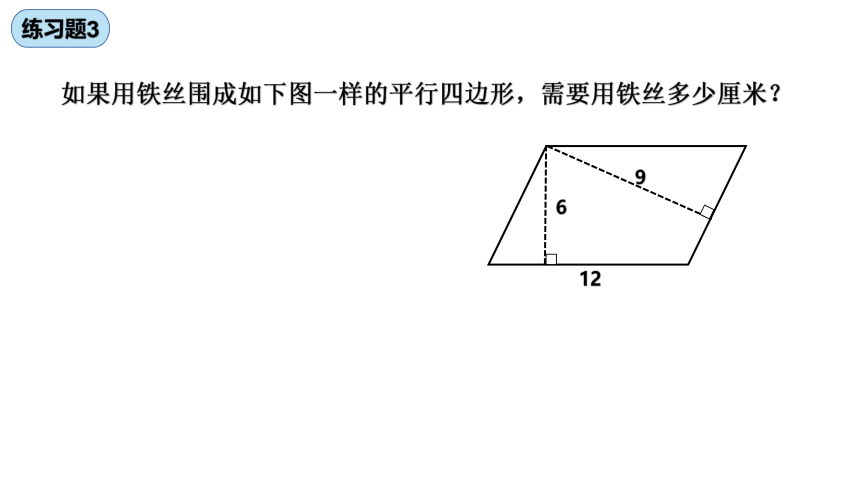
练习题3
如果用铁丝围成如下图一样的平行四边形,需要用铁丝多少厘米?
12
6
9
二、“总-空白”法求阴影面积
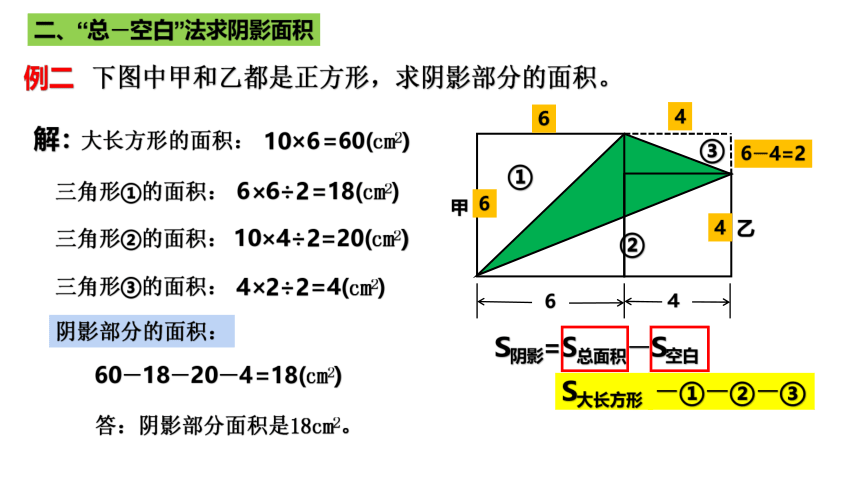
例二 下图中甲和乙都是正方形,求阴影部分的面积。
4
6
甲
乙
S阴影=S总面积-S空白
S大长方形
①
②
③
-①-②-③
解:
三角形①的面积:
6
6
6×6÷2
=18(cm2)
三角形②的面积:
10×4÷2
4
=20(cm2)
大长方形的面积:
10×6
=60(cm2)
三角形③的面积:
4
6-4=2
4×2÷2
=4(cm2)
阴影部分的面积:
60-18-20-4
=18(cm2)
答:阴影部分面积是18cm2。
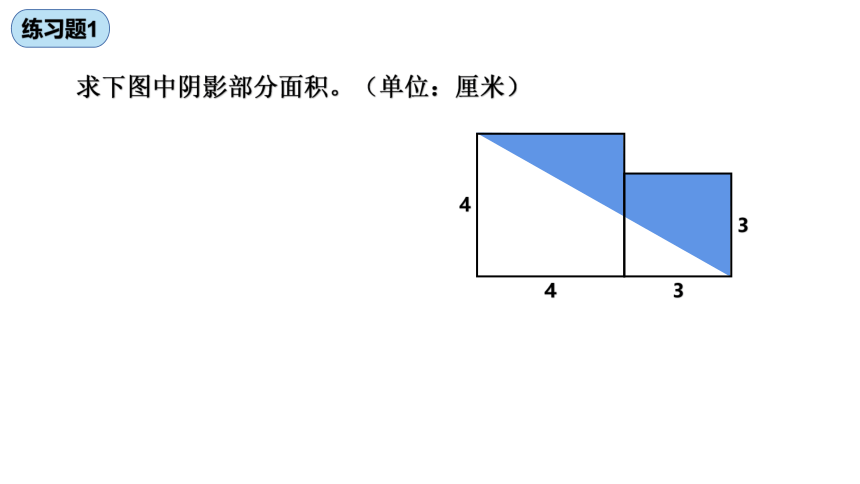
练习题1
求下图中阴影部分面积。(单位:厘米)
4
4
3
3
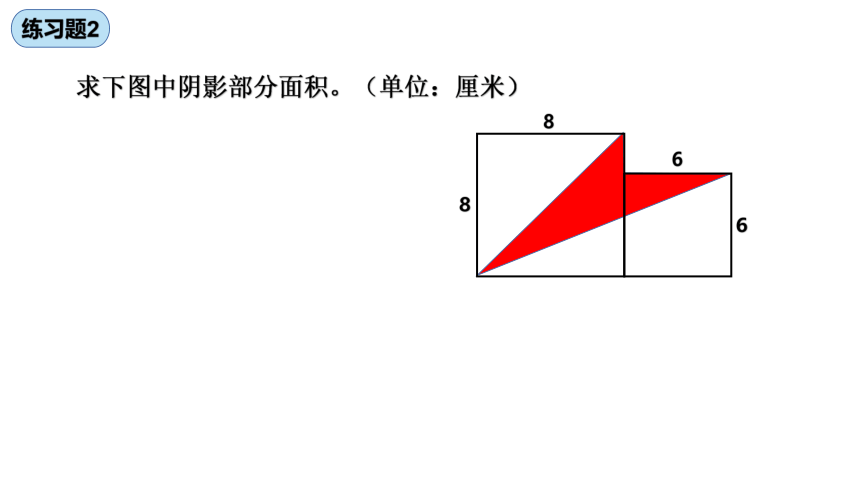
练习题2
求下图中阴影部分面积。(单位:厘米)
8
8
6
6
练习题3
如图所示,一个长方形草坪,长20米,宽14米,中间有一条宽
2米的曲折小路,求路的面积。
20米
14米
2
2
三、利用“差不变性质”求阴影面积
例三 如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,
求CE的长度。
4
4
A
B
C
D
E
F
甲
乙
?
解:
S甲-S乙=6cm2
①
差不变的性质
(S甲+①)
(S乙+①)
-
=6cm2
S正方形
S三角形ABE
-
=6cm2
正方形的面积:
4×4
=16(cm2)
三角形ABE的面积:
16-6
=10(cm2)
底BE的长度为:
10×2÷4
=5(cm)
CE的长度为:
5-4
=1(cm)
答:CE的长度是1cm。
练习题1
长方形ABCD是一个长为10厘米,宽为6厘米的长方形,三角形ADE的
面积比三角形CEF的面积大10平方厘米。求CF的长度是多少厘米?
A
B
C
D
E
F
10
6
练习题2
平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8
厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米。求CF的长?
A
B
C
D
F
G
E
练习题3
正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求:
(1)三角形DEF的面积。(2)CF的长。
A
B
C
D
E
F
?
四、梯形中的“等高”应用
例四 两条对角线把梯形ABCD分割成四个三角形。已知两个三角形的
面积(如图所示),求另两个三角形的面积各是多少?(单位:厘米)
A
D
B
C
O
6
12
解:
S三角形ABC
S三角形DBC
=
①
S三角形ABC-①
S三角形DBC-①
=
S三角形ABO
S三角形CDO
=
=12(cm2)
12
?
底CO的长度是底AO的2倍,
三角形BOC的面积是三角形AOB面积的2倍
三角形BOC的面积:
12×2
=24(cm2)
24
答:另两个三角形的面积分别是12cm2,24cm2。
练习题1
如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的
面积是多少平方厘米?
A
B
C
D
O
练习题2
A
B
C
D
O
下图梯形中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的
面积比三角形AOD的面积大多少平方厘米?
课后作业
1.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求
阴影部分的面积。
A
B
C
D
E
F
8
6
2.下图的梯形中,阴影部分面积是100平方厘米,求梯形的面积。
10厘米
25厘米
3.下图是一块长方形草地,长方形长为16米,宽为12米,中间有一条
宽为2米的道路,求草地(阴影部分)的面积。
4.下图长方形中,E、F分别是AD和DC的中点。已知AB=10厘米,
BC=8厘米,那么阴影部分的面积是多少平方厘米?
A
B
C
D
E
F
10
8
5.下图中,乙三角形的面积比甲三角形的面积大4平方厘米,求m的值。
甲
乙
4
m
5
48平方厘米
6.求下图中阴影部分面积。(单位:厘米)
8
15
多边形面积的计算
在数学课上我们已经掌握了几种基本图形的面积计算方法:
正方形的面积=
边长×边长
S=a2
长方形的面积=
长×宽
S=ab
平行四边形的面积=
底×高
S=ah
三角形的面积=
底×高÷2
S=ah÷2
梯形的面积=
(上底+下底)×高÷2
S=(a+b)h÷2
例一 已知平行四边形的面积是28平方厘米,求阴影部分的面积。
一、直接利用面积公式计算面积
5厘米
4厘米
S阴影=S三角形
=底×高÷2
底
?
4
S平行四边形=
底×高
28
?
4
解:
平行四边形的底:
28÷4
=7(cm)
三角形的底:
7-5
=2(cm)
三角形面积:
2×4÷2
=4(cm2)
2厘米
答:阴影部分面积是4cm2。
练习题1
已知平行四边形的面积是48平方厘米,求阴影部分的面积。
5厘米
6厘米
练习题2
下图的梯形中,阴影部分面积是150平方厘米,求梯形的面积。
15厘米
25厘米
练习题3
如果用铁丝围成如下图一样的平行四边形,需要用铁丝多少厘米?
12
6
9
二、“总-空白”法求阴影面积
例二 下图中甲和乙都是正方形,求阴影部分的面积。
4
6
甲
乙
S阴影=S总面积-S空白
S大长方形
①
②
③
-①-②-③
解:
三角形①的面积:
6
6
6×6÷2
=18(cm2)
三角形②的面积:
10×4÷2
4
=20(cm2)
大长方形的面积:
10×6
=60(cm2)
三角形③的面积:
4
6-4=2
4×2÷2
=4(cm2)
阴影部分的面积:
60-18-20-4
=18(cm2)
答:阴影部分面积是18cm2。
练习题1
求下图中阴影部分面积。(单位:厘米)
4
4
3
3
练习题2
求下图中阴影部分面积。(单位:厘米)
8
8
6
6
练习题3
如图所示,一个长方形草坪,长20米,宽14米,中间有一条宽
2米的曲折小路,求路的面积。
20米
14米
2
2
三、利用“差不变性质”求阴影面积
例三 如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,
求CE的长度。
4
4
A
B
C
D
E
F
甲
乙
?
解:
S甲-S乙=6cm2
①
差不变的性质
(S甲+①)
(S乙+①)
-
=6cm2
S正方形
S三角形ABE
-
=6cm2
正方形的面积:
4×4
=16(cm2)
三角形ABE的面积:
16-6
=10(cm2)
底BE的长度为:
10×2÷4
=5(cm)
CE的长度为:
5-4
=1(cm)
答:CE的长度是1cm。
练习题1
长方形ABCD是一个长为10厘米,宽为6厘米的长方形,三角形ADE的
面积比三角形CEF的面积大10平方厘米。求CF的长度是多少厘米?
A
B
C
D
E
F
10
6
练习题2
平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8
厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米。求CF的长?
A
B
C
D
F
G
E
练习题3
正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求:
(1)三角形DEF的面积。(2)CF的长。
A
B
C
D
E
F
?
四、梯形中的“等高”应用
例四 两条对角线把梯形ABCD分割成四个三角形。已知两个三角形的
面积(如图所示),求另两个三角形的面积各是多少?(单位:厘米)
A
D
B
C
O
6
12
解:
S三角形ABC
S三角形DBC
=
①
S三角形ABC-①
S三角形DBC-①
=
S三角形ABO
S三角形CDO
=
=12(cm2)
12
?
底CO的长度是底AO的2倍,
三角形BOC的面积是三角形AOB面积的2倍
三角形BOC的面积:
12×2
=24(cm2)
24
答:另两个三角形的面积分别是12cm2,24cm2。
练习题1
如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的
面积是多少平方厘米?
A
B
C
D
O
练习题2
A
B
C
D
O
下图梯形中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的
面积比三角形AOD的面积大多少平方厘米?
课后作业
1.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求
阴影部分的面积。
A
B
C
D
E
F
8
6
2.下图的梯形中,阴影部分面积是100平方厘米,求梯形的面积。
10厘米
25厘米
3.下图是一块长方形草地,长方形长为16米,宽为12米,中间有一条
宽为2米的道路,求草地(阴影部分)的面积。
4.下图长方形中,E、F分别是AD和DC的中点。已知AB=10厘米,
BC=8厘米,那么阴影部分的面积是多少平方厘米?
A
B
C
D
E
F
10
8
5.下图中,乙三角形的面积比甲三角形的面积大4平方厘米,求m的值。
甲
乙
4
m
5
48平方厘米
6.求下图中阴影部分面积。(单位:厘米)
8
15
