2021-2022学年度北师大版九年级数学上册第四章课件 4.2 平行线分线段成比例(共23张PPT)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学上册第四章课件 4.2 平行线分线段成比例(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
BS九(上)
教学课件
第四章 图形的相似
4.2 平行线分线段成比例
1.了解平行线分线段成比例的基本事实及其推论.(重点)
2.会用平行线分线段成比例及其推论解决相关问题.(难点)
学习目标
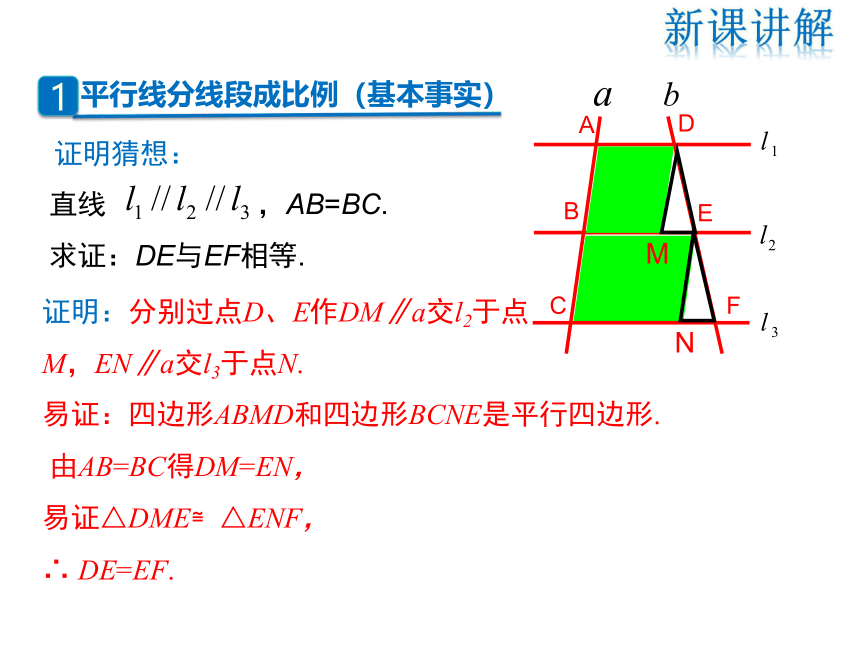
下图是一架梯子的示意图,由生活常识可以知道:AA1、BB1、CC1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
DE=EF
D
F
E
观察与猜想:
N
E
A
B
C
D
F
直线 ,AB=BC.
求证:DE与EF相等.
M
证明:分别过点D、E作DM∥a交l2于点
M,EN∥a交l3于点N.
易证:四边形ABMD和四边形BCNE是平行四边形.
由AB=BC得DM=EN,
易证△DME≌△ENF,
∴ DE=EF.
证明猜想:
1
平行线分线段成比例(基本事实)
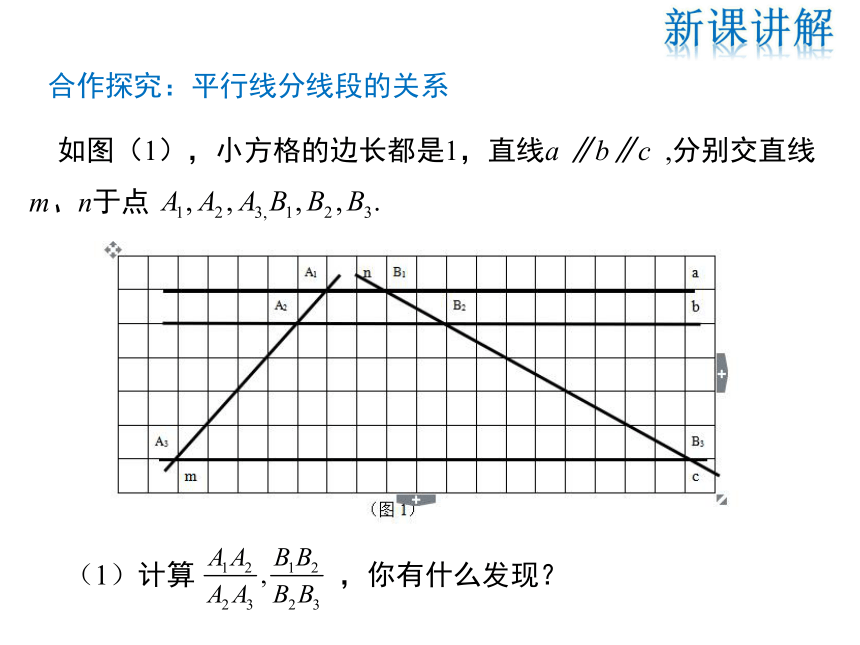
如图(1),小方格的边长都是1,直线a ∥b∥c ,分别交直线m、n于点
(1)计算 ,你有什么发现?
合作探究:平行线分线段的关系
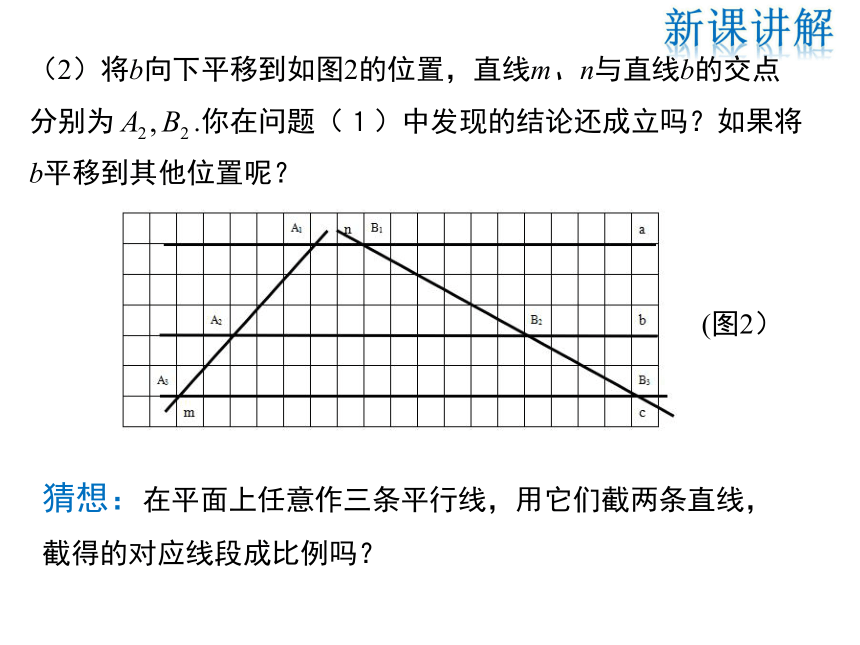
(2)将b向下平移到如图2的位置,直线m、n与直线b的交点分别为 .你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢?
(图2)
猜想:在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
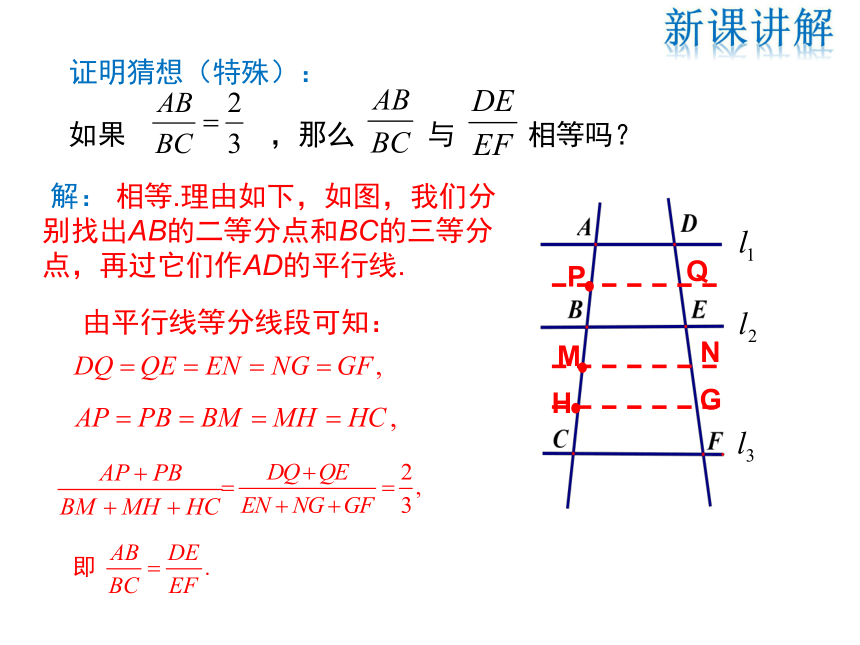
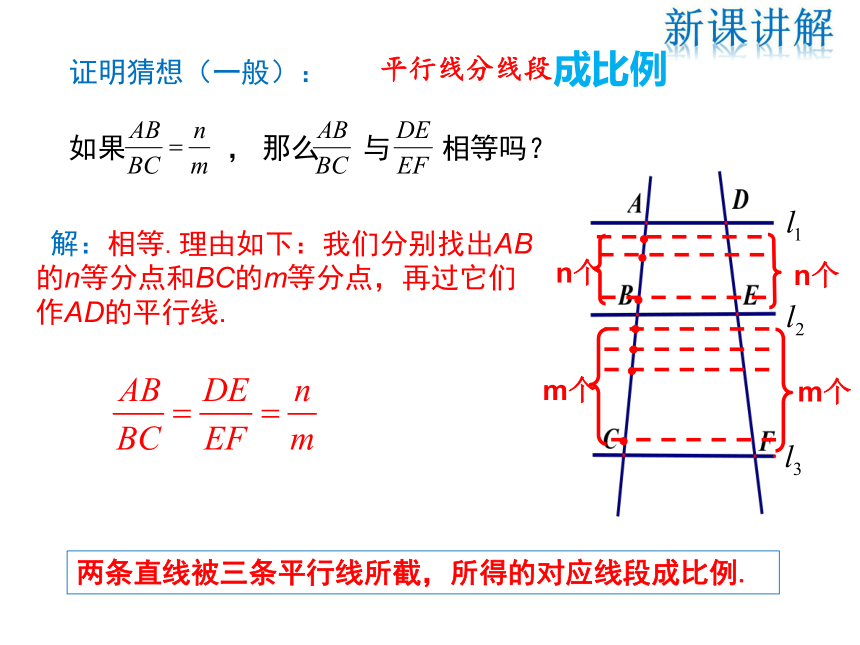
如果 ,那么 与 相等吗?
解: 相等.理由如下,如图,我们分别找出AB的二等分点和BC的三等分点,再过它们作AD的平行线.
P
M
H
Q
N
G
由平行线等分线段可知:
证明猜想(特殊):
如果 , 那么 与 相等吗?
解:相等.理由如下:我们分别找出AB的n等分点和BC的m等分点,再过它们作AD的平行线.
平行线分线段
两条直线被三条平行线所截,所得的对应线段成比例.
成比例
n个
m个
n个
m个
证明猜想(一般):
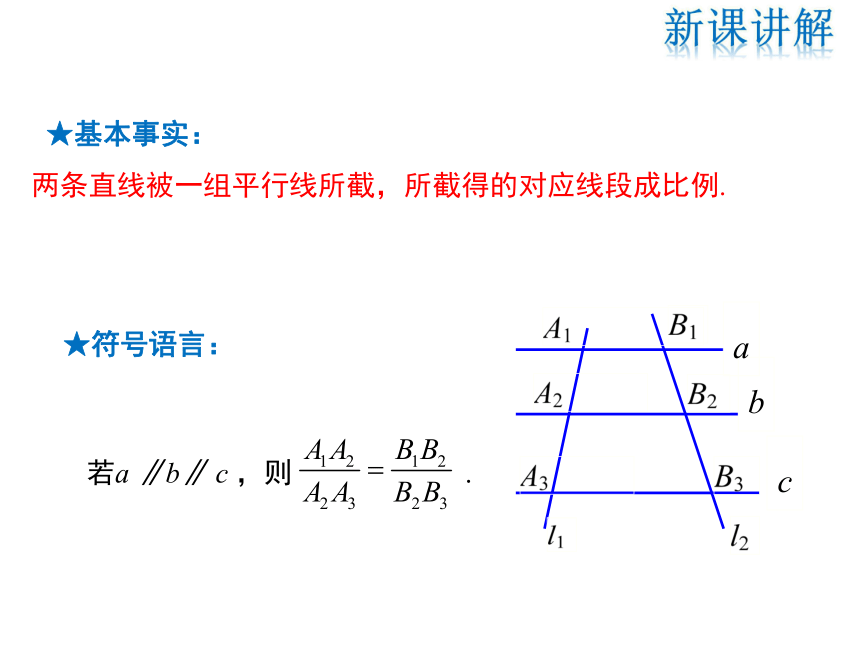
★基本事实:
两条直线被一组平行线所截,所截得的对应线段成比例.
★符号语言:
若a ∥b∥ c ,则 .
b
c
a
1.直线AB//CD//EF,若AC=3,CE=4,
则 ,
2.直线 ,若AC=4,CE=6,
则BD=3 ,BF=
练一练:
l2
l1
l2
l3
l4
l5
l1
A
B
C
D
E
A
B
C
D
E
l3
l4
l5
C
A
B
D
E
A
B
C
D
E
找一找:如图2、图3,l3∥ l4∥l5,请指出成比例的线段.
猜想:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
图2
图3
平行线分线段成比例定理的推论
2
如图,在△ABC中,已知DE∥BC,求证:
及 .
A
B
C
D
E
M
N
如图,过点A作直线MN,使
MN//DE.
∵DE//BC,
∴MN//DE//BC.
因此AB、AC被一组平行线MN、DE、BC所截.
证明猜想:
同时还可以得到
则由平行线分线段成比例可知
归纳总结:
平行线分线段成比例的推论:
平行于三角形一边的直线与其他两边(或其延长线)
相交,截得的对应线段成比例.
如图,在△ABC中,E、F分别是AB和AC的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AE = 7, EB = 5 , FC = 4,
∴
例1
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AB = 10 , AE = 6 , AF = 5,
∴
∴FC=AC – AF =
如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE//BC,EF//AB,若AD=2BD.
(1)求 的值. (2)求证: .
A
B
C
D
E
F
解:(1)∵DE//BC,EF//AB,
又AD=2BD,
(2)∵DE//BC,EF//AB,
∴四边形BDEF是平行四边形,∴DE=BF.
例2
1.如图,已知l1∥l2∥l3,下列比例式中错误的是( )
A. B.
C. D.
D
3.在△ABC中,ED//AB,若 ,
则
2.如图,DE∥BC,已知
A
B
C
E
D
A
B
C
D
E
4.已知DE//BC, AB=15,AC=9,BD=4 ,求AE的长.
解:
∵ DE∥BC,
AB AC
BD CE
∴
——
——.
=
即
5.如图,AB=AC,AD⊥BC于点D,M是AD的中点,CM交AB于
点P,DN ∥CP.若AB=6 cm,求AP的长.
解:∵AB=AC,AD⊥BC于点D,
M是AD的中点,
∴DB=DC,AM=MD.
∵DN ∥CP,
又∵AB=6 cm,
∴AP=2 cm.
平行线分线
段成比例
平行于三角形一边的直线与其他两边相交,
截得的对应线段成比例
基本事实
推论
两条直线被一组平行线所截,所得的对应线
段成比例
BS九(上)
教学课件
第四章 图形的相似
4.2 平行线分线段成比例
1.了解平行线分线段成比例的基本事实及其推论.(重点)
2.会用平行线分线段成比例及其推论解决相关问题.(难点)
学习目标
下图是一架梯子的示意图,由生活常识可以知道:AA1、BB1、CC1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
DE=EF
D
F
E
观察与猜想:
N
E
A
B
C
D
F
直线 ,AB=BC.
求证:DE与EF相等.
M
证明:分别过点D、E作DM∥a交l2于点
M,EN∥a交l3于点N.
易证:四边形ABMD和四边形BCNE是平行四边形.
由AB=BC得DM=EN,
易证△DME≌△ENF,
∴ DE=EF.
证明猜想:
1
平行线分线段成比例(基本事实)
如图(1),小方格的边长都是1,直线a ∥b∥c ,分别交直线m、n于点
(1)计算 ,你有什么发现?
合作探究:平行线分线段的关系
(2)将b向下平移到如图2的位置,直线m、n与直线b的交点分别为 .你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢?
(图2)
猜想:在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
如果 ,那么 与 相等吗?
解: 相等.理由如下,如图,我们分别找出AB的二等分点和BC的三等分点,再过它们作AD的平行线.
P
M
H
Q
N
G
由平行线等分线段可知:
证明猜想(特殊):
如果 , 那么 与 相等吗?
解:相等.理由如下:我们分别找出AB的n等分点和BC的m等分点,再过它们作AD的平行线.
平行线分线段
两条直线被三条平行线所截,所得的对应线段成比例.
成比例
n个
m个
n个
m个
证明猜想(一般):
★基本事实:
两条直线被一组平行线所截,所截得的对应线段成比例.
★符号语言:
若a ∥b∥ c ,则 .
b
c
a
1.直线AB//CD//EF,若AC=3,CE=4,
则 ,
2.直线 ,若AC=4,CE=6,
则BD=3 ,BF=
练一练:
l2
l1
l2
l3
l4
l5
l1
A
B
C
D
E
A
B
C
D
E
l3
l4
l5
C
A
B
D
E
A
B
C
D
E
找一找:如图2、图3,l3∥ l4∥l5,请指出成比例的线段.
猜想:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
图2
图3
平行线分线段成比例定理的推论
2
如图,在△ABC中,已知DE∥BC,求证:
及 .
A
B
C
D
E
M
N
如图,过点A作直线MN,使
MN//DE.
∵DE//BC,
∴MN//DE//BC.
因此AB、AC被一组平行线MN、DE、BC所截.
证明猜想:
同时还可以得到
则由平行线分线段成比例可知
归纳总结:
平行线分线段成比例的推论:
平行于三角形一边的直线与其他两边(或其延长线)
相交,截得的对应线段成比例.
如图,在△ABC中,E、F分别是AB和AC的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AE = 7, EB = 5 , FC = 4,
∴
例1
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AB = 10 , AE = 6 , AF = 5,
∴
∴FC=AC – AF =
如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE//BC,EF//AB,若AD=2BD.
(1)求 的值. (2)求证: .
A
B
C
D
E
F
解:(1)∵DE//BC,EF//AB,
又AD=2BD,
(2)∵DE//BC,EF//AB,
∴四边形BDEF是平行四边形,∴DE=BF.
例2
1.如图,已知l1∥l2∥l3,下列比例式中错误的是( )
A. B.
C. D.
D
3.在△ABC中,ED//AB,若 ,
则
2.如图,DE∥BC,已知
A
B
C
E
D
A
B
C
D
E
4.已知DE//BC, AB=15,AC=9,BD=4 ,求AE的长.
解:
∵ DE∥BC,
AB AC
BD CE
∴
——
——.
=
即
5.如图,AB=AC,AD⊥BC于点D,M是AD的中点,CM交AB于
点P,DN ∥CP.若AB=6 cm,求AP的长.
解:∵AB=AC,AD⊥BC于点D,
M是AD的中点,
∴DB=DC,AM=MD.
∵DN ∥CP,
又∵AB=6 cm,
∴AP=2 cm.
平行线分线
段成比例
平行于三角形一边的直线与其他两边相交,
截得的对应线段成比例
基本事实
推论
两条直线被一组平行线所截,所得的对应线
段成比例
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
