2021-2022学年度北师大版九年级数学上册4.7 第1课时 相似三角形中的对应线段之比课件 (共25张PPT)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学上册4.7 第1课时 相似三角形中的对应线段之比课件 (共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 13:04:07 | ||
图片预览



文档简介
(共25张PPT)
BS九(上)
教学课件
第四章 图形的相似
4.7 相似三角形的性质
第1课时 相似三角形中的对应线段之比
1.明确相似三角形中对应线段与相似比的关系.
(重点)
2.能熟练运用相似三角形的性质解决实际问题.(难点)
学习目标
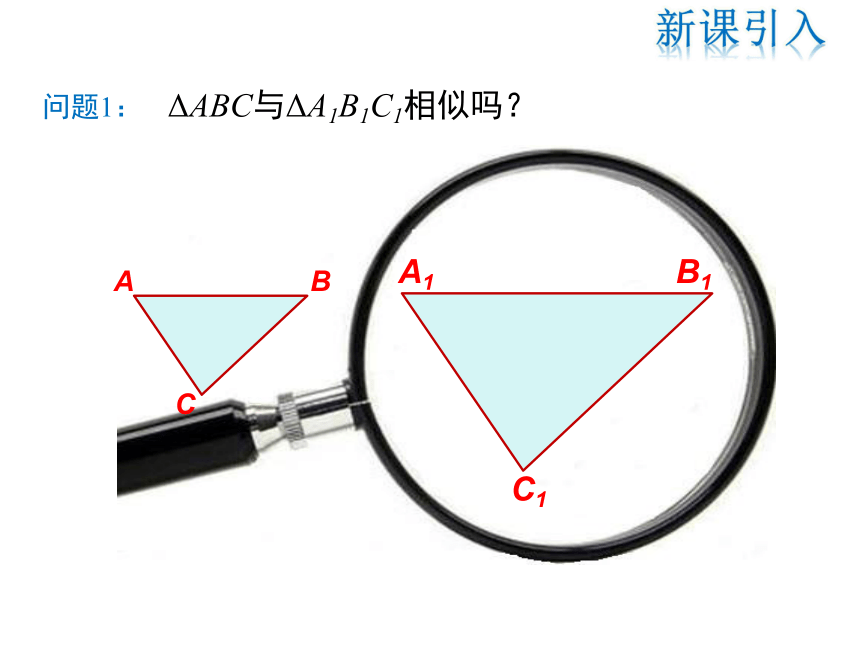
A
C
B
A1
C1
B1
问题1: ΔABC与ΔA1B1C1相似吗?
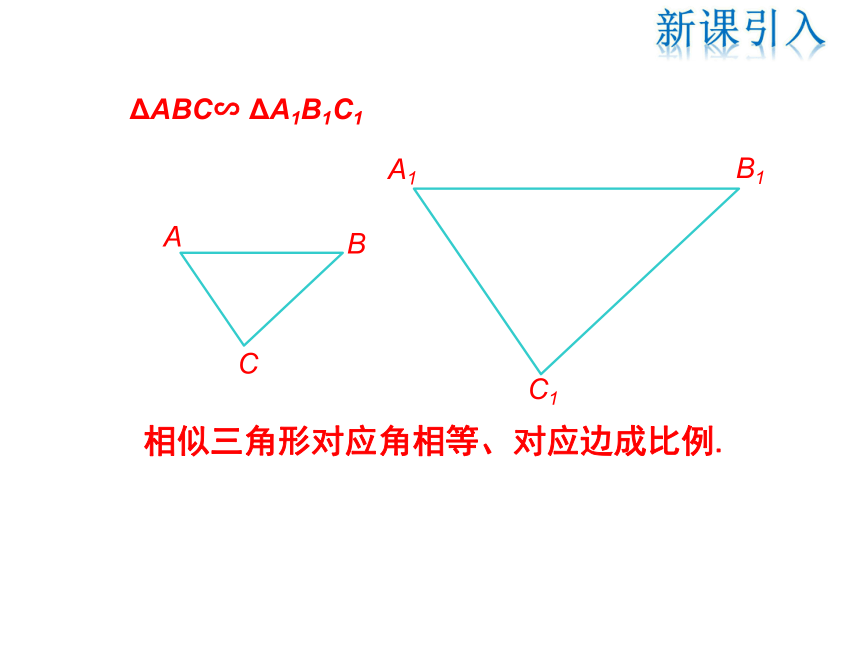
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
ΔABC∽ ΔA1B1C1
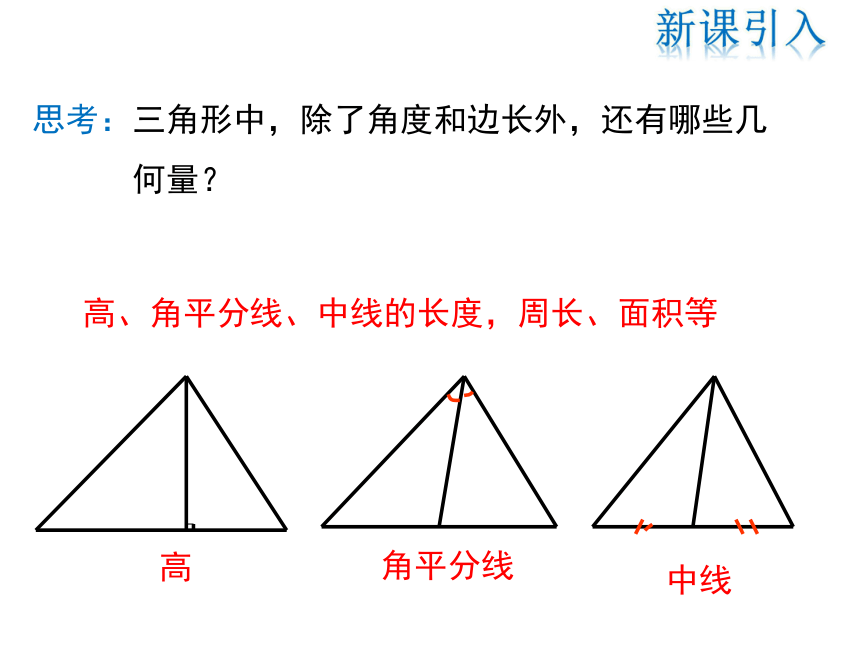
思考:三角形中,除了角度和边长外,还有哪些几
何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
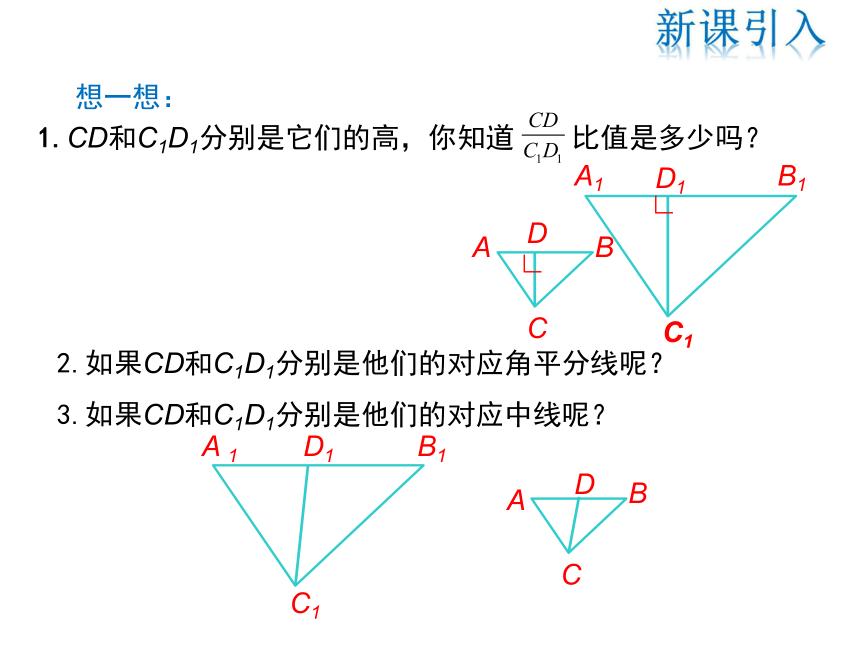
A
C
B
D
∟
A1
C1
B1
D1
∟
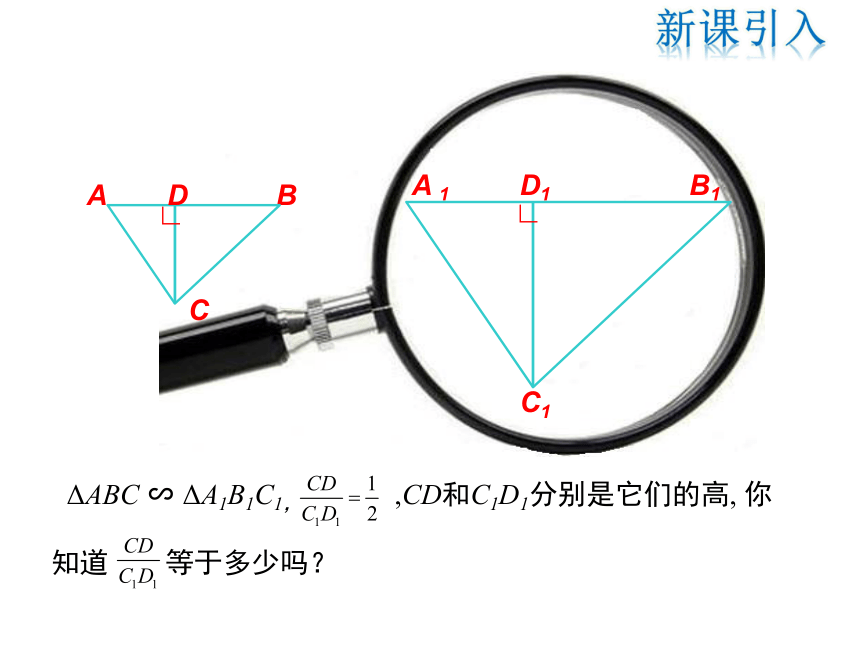
1.CD和C1D1分别是它们的高,你知道 比值是多少吗?
2.如果CD和C1D1分别是他们的对应角平分线呢?
3.如果CD和C1D1分别是他们的对应中线呢?
A
C
B
D
A 1
C1
B1
D1
想一想:
D1
A 1
C1
B1
∟
A
C
B
D
∟
ΔABC ∽ ΔA1B1C1, ,CD和C1D1分别是它们的高, 你知道 等于多少吗?
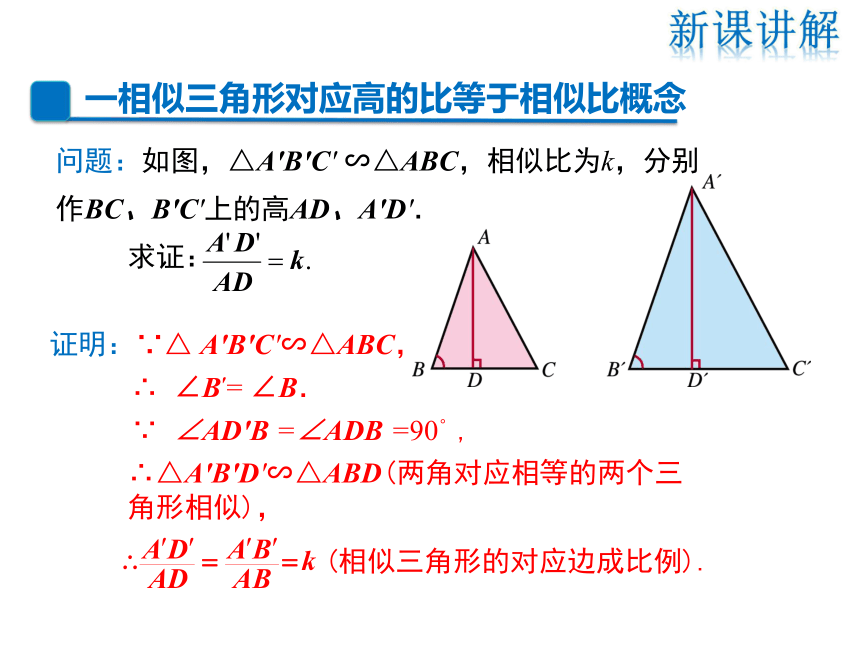
证明:∵△ A′B′C′∽△ABC,
∴ ∠B′= ∠B.
∵ ∠AD′B =∠ADB =90°,
∴△A′B′D′∽△ABD(两角对应相等的两个三角形相似),
(相似三角形的对应边成比例).
问题:如图,△A′B′C′ ∽△ABC,相似比为k,分别作BC、B′C′上的高AD、A′D′.
求证:
一相似三角形对应高的比等于相似比概念
由此得到:
相似三角形对应高的比等于相似比.
类似地,我们可以得到其余两组对应边上的高的比也等于相似比.
如图,AD是ΔABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=60 cm,AD=40 cm,四边形PQRS是正方形.
(1)AE是Δ ASR的高吗?为什么?
(2) ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
例1
(1)AE是ΔASR的高吗?为什么?
解: AE是ΔASR的高.
理由如下:
∵AD是ΔABC的高,
∴ ∠ADC=90 °.
∵四边形PQRS是正方形,
∴SR ∥BC,
∴∠AER=∠ADC=90 °,
∴ AE是ΔASR的高.
BC=60 cm,AD=40 cm,四边形PQRS是正方形.
S
R
Q
P
E
D
C
B
A
BC=60 cm,AD=40 cm,四边形PQRS是正方形.
(2) ΔASR与ΔABC相似吗?为什么?
解: ΔASR与ΔABC相似 . 理由如下:
∵ SR∥BC,
∴ ΔASR∽ΔABC.
S
R
Q
P
E
D
C
B
A
BC=60 cm,AD=40 cm,四边形PQRS是正方形.
(3)求正方形PQRS的边长.
是方程思想哦!
解:∵ ΔASR ∽ ΔABC,
AE、AD分别是ΔASR 和ΔABC
对应边上的高,
设正方形PQRS的边长为x cm,
则SR=DE=x cm,AE=(40-x)cm.
∴ 解得x=24.
∴正方形PQRS的边长为24 cm.
S
R
Q
P
E
D
C
B
A
解:当SR=2SP,设SP=x cm,则SR=2xcm,
得到 所以x=2,2x=4,
2×4=8 cm2.
S
R
Q
P
E
D
C
B
A
如图,AD是ΔABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=5 cm,AD=10 cm,若矩形PQRS的长是宽的2倍,你能求出这个矩形的面积吗?
当SP=2SR,SR=x cm,则SP=2x cm,
得到 所以x=2.5,2x=5,
2.5×5=12.5 cm2 .
变式:
问题:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
2
相似三角形角平分线的比、对应中线的比
已知:△ABC∽△A′B′C′,相似比为k,即
求证:
证明:∵ △ABC∽△A′B′C′,
∴ ∠A′B′C′= ∠ABC, ∠B′A′C′= ∠BAC.
又BE、B'E'分别为对应角的平分线,
∴ △ABE∽△A′B′E′,
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想1:
相似三角形对应的中线的比也等于相似比.
同学们可以试着用同样的方法求证三角形对应边上的角平分中线的比等于相似比.
已知△ABC∽△A′B′C′,相似比为k,即
求证:
证明:∵ △ABC∽△A′B′C′,
∴ ∠A′B′C′= ∠ABC, .
又AD、AD′分别为对应边的中线.
∴ △ABD∽△A′B′D′,
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想2:
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
两个相似三角形的两条对应边的长分别是6 cm和8 cm,如果它们对应的两条角平分线的和为42 cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为x cm,
则由相似性质有
解得x=18.
较长的角平分线长为24 cm.
故这两条角平分线的长分别为18 cm,24 cm.
例2
3.两个相似三角形对应中线的比为1:4 ,则对应高的比为______ .
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶ 3
1.两个相似三角形的相似比为1:2, 则对应高的比为_________, 则对应中线的比为_________.
解:∵ △ABC∽△DEF,
解得EH=3.2(cm).
即EH的长为3.2cm.
A
G
B
C
D
E
F
H
(相似三角形对应角平
线的比等于相似比),
4.已知△ABC∽△DEF,BG、EH分别为△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
5.如图,AD是△ABC的高,AD=h, 点R在AC边上,点S在AB边上,SR⊥AD,垂足为点E.当 时,求DE的长.如果
呢?
∴△ASR∽△ABC,
解:∵SR⊥AD,BC⊥AD,∴SR∥BC,
B
A
E
R
C
D
S
∴∠ASR=∠B,∠ARS=∠C,
S
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
BS九(上)
教学课件
第四章 图形的相似
4.7 相似三角形的性质
第1课时 相似三角形中的对应线段之比
1.明确相似三角形中对应线段与相似比的关系.
(重点)
2.能熟练运用相似三角形的性质解决实际问题.(难点)
学习目标
A
C
B
A1
C1
B1
问题1: ΔABC与ΔA1B1C1相似吗?
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
ΔABC∽ ΔA1B1C1
思考:三角形中,除了角度和边长外,还有哪些几
何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
A
C
B
D
∟
A1
C1
B1
D1
∟
1.CD和C1D1分别是它们的高,你知道 比值是多少吗?
2.如果CD和C1D1分别是他们的对应角平分线呢?
3.如果CD和C1D1分别是他们的对应中线呢?
A
C
B
D
A 1
C1
B1
D1
想一想:
D1
A 1
C1
B1
∟
A
C
B
D
∟
ΔABC ∽ ΔA1B1C1, ,CD和C1D1分别是它们的高, 你知道 等于多少吗?
证明:∵△ A′B′C′∽△ABC,
∴ ∠B′= ∠B.
∵ ∠AD′B =∠ADB =90°,
∴△A′B′D′∽△ABD(两角对应相等的两个三角形相似),
(相似三角形的对应边成比例).
问题:如图,△A′B′C′ ∽△ABC,相似比为k,分别作BC、B′C′上的高AD、A′D′.
求证:
一相似三角形对应高的比等于相似比概念
由此得到:
相似三角形对应高的比等于相似比.
类似地,我们可以得到其余两组对应边上的高的比也等于相似比.
如图,AD是ΔABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=60 cm,AD=40 cm,四边形PQRS是正方形.
(1)AE是Δ ASR的高吗?为什么?
(2) ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
例1
(1)AE是ΔASR的高吗?为什么?
解: AE是ΔASR的高.
理由如下:
∵AD是ΔABC的高,
∴ ∠ADC=90 °.
∵四边形PQRS是正方形,
∴SR ∥BC,
∴∠AER=∠ADC=90 °,
∴ AE是ΔASR的高.
BC=60 cm,AD=40 cm,四边形PQRS是正方形.
S
R
Q
P
E
D
C
B
A
BC=60 cm,AD=40 cm,四边形PQRS是正方形.
(2) ΔASR与ΔABC相似吗?为什么?
解: ΔASR与ΔABC相似 . 理由如下:
∵ SR∥BC,
∴ ΔASR∽ΔABC.
S
R
Q
P
E
D
C
B
A
BC=60 cm,AD=40 cm,四边形PQRS是正方形.
(3)求正方形PQRS的边长.
是方程思想哦!
解:∵ ΔASR ∽ ΔABC,
AE、AD分别是ΔASR 和ΔABC
对应边上的高,
设正方形PQRS的边长为x cm,
则SR=DE=x cm,AE=(40-x)cm.
∴ 解得x=24.
∴正方形PQRS的边长为24 cm.
S
R
Q
P
E
D
C
B
A
解:当SR=2SP,设SP=x cm,则SR=2xcm,
得到 所以x=2,2x=4,
2×4=8 cm2.
S
R
Q
P
E
D
C
B
A
如图,AD是ΔABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=5 cm,AD=10 cm,若矩形PQRS的长是宽的2倍,你能求出这个矩形的面积吗?
当SP=2SR,SR=x cm,则SP=2x cm,
得到 所以x=2.5,2x=5,
2.5×5=12.5 cm2 .
变式:
问题:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
2
相似三角形角平分线的比、对应中线的比
已知:△ABC∽△A′B′C′,相似比为k,即
求证:
证明:∵ △ABC∽△A′B′C′,
∴ ∠A′B′C′= ∠ABC, ∠B′A′C′= ∠BAC.
又BE、B'E'分别为对应角的平分线,
∴ △ABE∽△A′B′E′,
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想1:
相似三角形对应的中线的比也等于相似比.
同学们可以试着用同样的方法求证三角形对应边上的角平分中线的比等于相似比.
已知△ABC∽△A′B′C′,相似比为k,即
求证:
证明:∵ △ABC∽△A′B′C′,
∴ ∠A′B′C′= ∠ABC, .
又AD、AD′分别为对应边的中线.
∴ △ABD∽△A′B′D′,
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想2:
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
两个相似三角形的两条对应边的长分别是6 cm和8 cm,如果它们对应的两条角平分线的和为42 cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为x cm,
则由相似性质有
解得x=18.
较长的角平分线长为24 cm.
故这两条角平分线的长分别为18 cm,24 cm.
例2
3.两个相似三角形对应中线的比为1:4 ,则对应高的比为______ .
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶ 3
1.两个相似三角形的相似比为1:2, 则对应高的比为_________, 则对应中线的比为_________.
解:∵ △ABC∽△DEF,
解得EH=3.2(cm).
即EH的长为3.2cm.
A
G
B
C
D
E
F
H
(相似三角形对应角平
线的比等于相似比),
4.已知△ABC∽△DEF,BG、EH分别为△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
5.如图,AD是△ABC的高,AD=h, 点R在AC边上,点S在AB边上,SR⊥AD,垂足为点E.当 时,求DE的长.如果
呢?
∴△ASR∽△ABC,
解:∵SR⊥AD,BC⊥AD,∴SR∥BC,
B
A
E
R
C
D
S
∴∠ASR=∠B,∠ARS=∠C,
S
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
