【高考自主招生】高中数学复习专题讲义:第3讲 微积分初步(PDF版含解析)
文档属性
| 名称 | 【高考自主招生】高中数学复习专题讲义:第3讲 微积分初步(PDF版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览



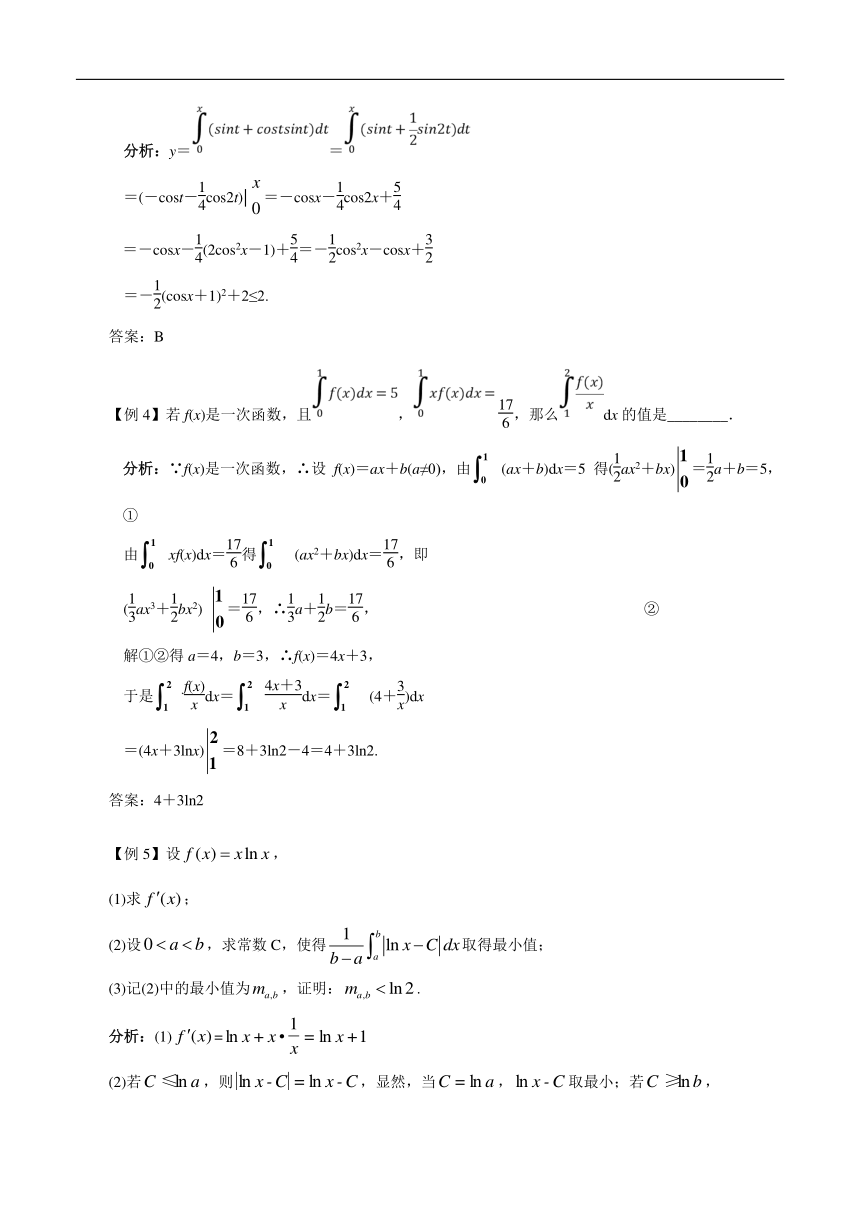
文档简介
第三讲 微积分初步
一、知识方法拓展
1、曲边梯形的定义
我们把由直线 x a, x b(a b), y 0和曲线 y f (x)所围成的图形称为曲边梯形。
2、曲边梯形的面积的求法
分割→近似代替(以直代曲)→求和→取极限
3、定积分的概念
一般地,设函数 f (x) 在区间[a,b]上连续,用分点
a = x0 < x1 < x2 < ...< xi-1 < xi < ...< xn = b
b - a
将区间[a,b]等分成 n 个小区间,每个小区间长度为Dx ( D = ),在每个小区间[xi-1 , xi ]上任取一x n
n n b a
点 xi (i = 1,2,...,n),作和式: S n f (xi ) x f ( i )
i 1 i 1 n
如果Dx 无限接近于0 (亦即n )时,上述和式 Sn 无限趋近于常数 S ,那么称该常数 S 为函数
b
f (x) 在区间[a,b]上的定积分。记为: S f (x)dx, a
其中 是积分号,b 是积分上限, a 是积分下限, f (x) 是被积函数, x 是积分变量,[a,b]是积分区
间, f (x)dx是被积式。
b
说明:(1)定积分 f (x)dx 是一个常数,可以是正数,也可以是负数,也可以是零,即 Sn 无限趋近a
b
的常数 S ( n 时)记为 f (x)dx ,而不是 Sn . a
(2)用定义求定积分的一般方法是:①分割: n 等分区间[a,b ];②近似代替:取点 i xi 1 , xi ;③
n b a b n b a
求和: f ( i );④取极限: f (x)dx lim f i n a n i 1 i 1 n
4、定积分的性质
根据定积分的定义,不难得出定积分的如下性质:
b b
性质 1 kf (x)dx k f (x)dx(k为常数) ; a a
b b b
性质 2 [ f1(x) f2(x)]dx f1(x)dx f2(x)dx ; a a a
b c b
性质 3 f (x)dx f (x)dx f (x)dx (其中a c b) a a c
5、定积分的几何意义
b
(1)从几何上看,如果在区间[a,b]上函数 f (x) 连续且恒有 f (x) 0,那么定积分 f x dx表示由直a
线 x a, x b(a b), y 0和曲线 y f (x)所围成的曲边梯形(如图中的阴影部分)的面积。
b
(2)从几何上看,如果在区间[a,b]上函数 f (x) 连续且恒有 f (x) 0,那么定积分 f x dx表示由直a
线 x a, x b(a b), y 0和曲线 y f (x)所围成的曲边梯形(如图中的阴影部分)的面积的相反数。
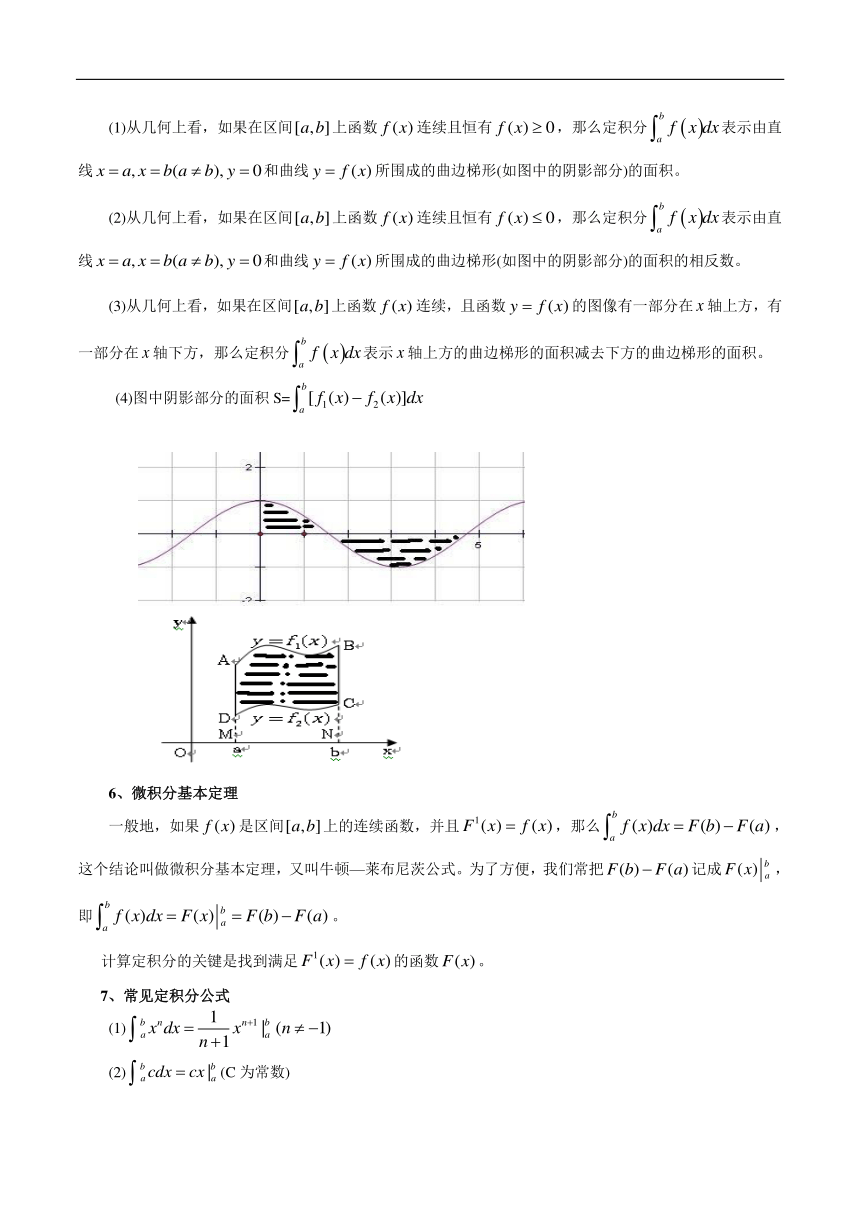
(3)从几何上看,如果在区间[a,b]上函数 f (x) 连续,且函数 y f (x) 的图像有一部分在 x 轴上方,有
b
一部分在 x 轴下方,那么定积分 f x dx表示 x 轴上方的曲边梯形的面积减去下方的曲边梯形的面积。 a
b
(4)图中阴影部分的面积 S= [ f1(x) f2(x)]dx a
6、微积分基本定理
b
1
一般地,如果 f (x) 是区间[a,b]上的连续函数,并且F (x) f (x),那么 f (x)dx F(b) F(a) ,a
b
这个结论叫做微积分基本定理,又叫牛顿—莱布尼茨公式。为了方便,我们常把F(b) F(a)记成F (x) a ,
b
f (x)dx F(x) b即 a F(b) F(a) 。 a
1
计算定积分的关键是找到满足 F (x) f (x)的函数F(x)。
7、常见定积分公式
b n 1 n 1 b
(1) a x dx x |a (n 1)n 1
b b
(2) a cdx cx |a (C 为常数)
b
(3) a sin xdx cos x |
b
a
b
(4) a cos xdx sin x |
b
a
b 1
(5) a dx ln x |
b
a (b a 0)
x
b x x b
(6) a e dx e |a
x
b x a b
(7) a a dx |a (a 0且a 1) ln a
二、热身练习
【例 1】计算下列各式:
6
2
(1) (x 1)dx =_____________; 0
分析:78
2
(2) (sin x 2)dx ___________; 2
分析: 8
e e
(3) (2
x )dx =_____________;
1 x
2e 2
分析: e
ln 2 ln 2
x
(4) 2 sin
2 dx =____________; 0
2
1
分析:
4 2
x2 (0 x 1)
2
【例 2】已知 f (x) ,则 0 f (x)dx =__________;
2 x (1 x 2)
分析:
【例 3】给出如下命题:
a b
③ dx b dt b a ( a,b 为常数且a b ); a
0 1
② 2 2
π
1 x dx 1 x dx ; 1 0 4
③曲线 y sin x , x [0,2π],与直线 y 0围成的两个封闭区域的面积之和为 2.
其中真命题的个数为( )
A.0 B.1 C. 2 D.3
分析:B
3
2
【例 4】 x 4 dx 等于( ) 0
21 22 23 25
A. B. C. D.
3 3 3 3
分析:C
三、真题讲解
【例 】已知 f (x) x (12t 4a)dt, F (a) 11 a 0[ f (x) 3a
2 ]dx ,求函数F (a) 的最小值.
分析: f (x) x a (12t 4a)dt
(6t2 4at) |x 6x2 a 4ax (6x
2 4a2) 6x2 4a 2a2
F (a) 1 0[ f (x) 3a
2 ] 1 (6x2 0 4ax a
2 )dx
3 2 2 1 3 2 2
(2x 2ax a x) |0 2.1x 2a.1 a .1
2 2
a 2a 2 (a 1) 1 1
当a 1时, F (a) 最小=1 当a 1时,F (a) 最小=1
【例 2】求在[0,2 ]上,由 x 轴及正弦曲线 y sin x 围成的图形的面积.
分析:作出 y sin x 在[0,2 ]上的图象如右 y
y sin x 与 x 轴交于 0、 、2 ,所
x
0 Л
s
2Л
求积 0 sin xdx |
2
sin xdx | ( cos x) |
( cos x) |2 0 4
【例 3】若 y= ,则 y 的最大值是( )
7
A.1 B.2 C.- D.0
2
分析:y= =
1 x 1 5
=(-cost- cos2t)| =-cosx- cos2x+
4 0 4 4
1 5 1 3
=-cosx- (2cos2x-1)+ =- cos2x-cosx+
4 4 2 2
1
=- (cosx+1)2+2≤2.
2
答案:B
17
【例 4】若 f(x)是一次函数,且 , ,那么 dx 的值是________.
6
1 1 1 1
分析:∵f(x)是一次函数,∴设 f(x)=ax+b(a≠0),由 (ax+b)dx=5 得( ax2+bx) = a+b=5, 0 2 0 2
①
1 17 1 17
由 xf(x)dx= 得 (ax2+bx)dx= ,即 0 6 0 6
1 1 1 17 1 1 17
( ax3+ bx2) = ,∴ a+ b= , ②
3 2 0 6 3 2 6
解①②得 a=4,b=3,∴f(x)=4x+3,
2 f(x) 2 4x+3 2 3
于是 dx= dx= (4+ )dx 1 x 1 x 1 x
2
=(4x+3lnx) =8+3ln2-4=4+3ln2.
1
答案:4+3ln2
【例 5】设 f (x) x ln x ,
(1)求 f (x);
1 b
(2)设0 a b,求常数 C,使得 ln x C dx取得最小值; b a a
(3)记(2)中的最小值为m ,证明: . a,b ma,b ln 2
1
分析:(1) f (x) = ln x + x = ln x +1
x
(2)若C ≤ln a ,则 ln x - C = ln x - C,显然,当C = ln a , ln x - C 取最小;若C ≥ln b,
则 ln x - C = C - ln x,当C = ln b,C - ln x 取最小
故不妨设 ln a ≤C ≤ln b
1 b
ln x C dx=
b a a
由(1)可知,
因
1 b
所以 ln x C dx
b a a
记 g(C) = a ln a + b ln b + 2ec - (a + b)C - (a + b)
c a + b
令 g ' (C) = 2e - (a+b) = 0,得C = ln
2
a + b 1 b
即C = ln , ln x C dx取最小值 2 b a a
a + b 1 b
(3)将C = ln 代入 ln x C dx 2 b a a
的右边,
1 a + b a + b
ma,b = [a ln a + b ln b - (a + b) ln ] < ln 2 a ln a + b ln b - (a + b) ln < (b - a) ln 2b - a 2 2
a ln a + b ln b + 2a ln 2 < (a + b) ln(a + b) 2a ln 2 < a ln(a + b) - a ln a + b ln(a + b) - blnb
b a
2a ln 2 < a ln(1+ ) + b ln(1+ )
a b
b b a
由于0 a b,故 +1 > 2,所以a ln(1+ ) > a ln 2,即只需证明b ln(1+ ) > a ln 2
a a b
a b a
a ln 2 < b ln(1+ ) ln 2 < ln(1+ )
b a b
a b a ln(1+ m)
1
令 = m∈(0,1),则 ln(1+ ) = = ln(1+ m)m
b a b m
1 1 1
函数 ln(1+ m) m 单调递减且m∈(0,1),所以 ln(1+ m)m > ln(1+1)1 = ln 2,得证
四、重点总结
1、能快速反应出常见的微分公式
2、利用牛顿-莱布尼兹公式计算
3、利用微积分求曲边梯形面积
五、强化训练
A 组
x 1, x 1
2
1、设 f x 1 ,求 f x dx。 x 2 0 , x 1
2
1 2
2 1 2 1 1 1 8
分析: f x dx x 1 dx x
2dx 2 x x x
3
0 0 1 2 2 6 1 30
2、已知 f(x)为偶函数且 ,则 等于( )
A.0 B.4 C.8 D.16
0 6
分析:原式= f(x)dx+ 6 f(x)dx, 0
∵原函数为偶函数,
∴在 y 轴两侧的图象对称,
∴对应的面积相等,即 8×2=16.
答案:D
3、函数 y=-x2+2x+1 与 y=1 相交形成一个闭合,则该闭合图形的面积
是( )
4
A.1 B. C. 3 D.2
3
分析:函数 y=-x2+2x+1 与 y=1 的两个交点为(0,1)和(2,1),所以闭合图
2 2 4
形的面积等于 (-x2+2x+1-1)dx=0 (-x
2+2x)dx= .
0 3
4
4、已知函数 y=x2与 y=kx(k>0)的图象所围成的阴影部分(如图所示)的面积为 ,则 k=________.
3
k kx2 x3 k k3 4
分析:直线方程与抛物线方程联立先求出积分区间为[0,k],再由 (kx-x2)dx=( - )y=x=2 =0 2 3 0 6 3
求得 k=2.
答案:2
1 x
2 , x 0 3
5、设 f x ,求 f x 2 dx 。
e x , x 0
1
分析:令 x 2 t ,则
3 1 0 1 7 1
f x 2 dx f t dt 1 t
2 dt t e dt 1 1 1 0 3 e
6、求曲线 y x2 , y x 及 y 2x所围成的平面图形的面积.
分析:作出 y x2 , y x 及 y 2x的图如右
y 2x x 2 x 0 B(2,4)
解方程组 得
y x
2
y 4 y 0
y=x
y x x 1 x 0
解方程组 得 A(1,1) 2
y x y 1 y 0 o x 1 2
1
所求面积 s 0 (2x x)dx
2
1 (2x x
2 )dx
1 2 2
0 xdx 1 (2x x )dx
1 1
x2 |1 (x2 x3) |2 0 1
2 3
7
6
2 ln 2 dt
7、若 ,求 x 。 x
e t 1 6
t 2 2u
分析:令 e 1 u ,则 t ln 1 u ,dt du
1 u 2
当 t 2ln 2时,u 3
x
当 t x时,u e 1
2ln 2 dt 3 2udu 3
∴ x t 2arctgu x ex 1 2 e 1e 1 1 u u
2 x arctg e 1
3 6
从而 x ln 2
x
x a
、已知 lim 4x2e 2x8 dx ,求常数 a 。 x x a a
x
2a
分析:左端 lim 1 2a e
x x a
右端 2x2e 2x d 2x 2x2de 2x a a
2 x2e 2x 2xe 2x dx
a a
2a2e 2a 2x 2 xde a
2a2e 2a 2 xe 2x e 2x dx
a a
2a 2 2a 1 e 2a
2 2a 2a
∴ 2a 2a 1 e e
解之a 0或a 1。
B 组
y = x2
1
9、在曲线 (x ≥0)上某一点 A 处作一切线使之与曲线以及 x 轴所围成图形的面积为 ,试求:
12
(1)切点 A 的坐标;
(2)过切点 A 的切线方程.
分析:(1)设切点 A(x 2 ,切线斜率为 k y 0,x0 ) x x 2x0 , 0
切线方程为 y x20 2x0(x x , 0)
x
令 y 0,得 x 0 .
2
x0 x
2 0 1 1
s 2 x dx x [x
2 (2x x x2 )]dx x30 0 0 ,
0 0
2 12 12
解得 x0 1, 切点 A 的坐标为 (1,1);
(2)将 A(1,1) 代入切线方程,得 y 1 2(x 1) ,
整理,得 y 2x 1.
即所求切线方程为 y 2x 1
答案:B
10、如图,设点 P 从原点沿曲线 y=x2向点 A(2,4)移动,记直线 OP、曲线 y=x2 及直线 x=2 所围成的
面积分别记为 S1,S2,若 S1=S2,求点 P 的坐标.
分析:设直线 OP 的方程为 y=kx, P 点的坐标为(x,y),
x 2
则 (kx-x2)dx= (x2-kx)dx, 0 x
1 1 x 1 1 2
即( kx2- x3) =( x3- kx2) ,
2 3 0 3 2 x
1 1 8 1 1
解得 kx2- x3= -2k-( x3- kx2),
2 3 3 3 2
4 4 4 16
解得 k= ,即直线 OP 的方程为 y= x,所以点 P 的坐标为( , ).
3 3 3 9
11、设 f(x)=
(1)当 0≤a≤1与 a>1 时,分别求 f(a);
(2)当 a≥0时,求 f(a)的最小值.
分析:(1)0≤a≤1时,
1
f(a)= |x2-a2|dx 0
a 1
= (a2-x2)dx+ (x2-a2)dx 0 a
1 a x3 1
=(a2x- x3) +( -a2x)
3 0 3 a
1 1 a3
=a3- a3-0+0+ -a2- +a3
3 3 3
4 1
= a3-a2+ .
3 3
当 a>1 时,
1
f(a)= (a2-x2)dx 0
1 1
=(a2x- x3)
3 0
1
=a2- .
3
4 3 2 1
a a (0≤ a≤1), 3 3
∴f(a)=
2 1a (a>1).
3
1 1 2
(2)当 a>1 时,由于 a2- 在[1,+∞)上是增函数,故 f(a)在[1,+∞)上的最小值是 f(1)=1- = .
3 3 3
当 a∈[0,1]时,f′(a)=4a2-2a=2a(2a-1),
1
由 f′(a)>0 知:a> 或 a<0,
2
1 1
故在[0, ]上递减,在[ ,1]上递增.
2 2
1 1
因此在[0,1]上,f(a)的最小值为 f( )= .
2 4
1
综上可知,f(x)在[0,+∞)上的最小值为 .
4
六、参考答案
A 组
1 2
2 1 2 1 1 1 8
1、分析: f
x dx x 1 dx x
2
dx x
2 x x
3
0 0 1 2 2 6 1 30
0 6
2、分析:原式= f(x)dx+ f(x)dx, 6 0
∵原函数为偶函数,
∴在 y 轴两侧的图象对称,
∴对应的面积相等,即 8×2=16.
答案:D
2
3、分析:函数 y=-x2+2x+1 与 y=1 的两个交点为(0,1)和(2,1),所以闭合图形的面积等于 (-x20
2 4
+2x+1-1)dx= (-x2+2x)dx= . 0 3
k kx2 x3 k k3
4、分析:直线方程与抛物线方程联立先求出积分区间为[0,k],再由 (kx-x2)dx=( -0 2 y= )3x20
=
6
4
= 求得 k=2.
3
答案:2
5、分析:令 x 2 t ,则
3 1 0 1 7 1
f x 2 dx f t dt 1 t
2
dt
t
1 1 1 e dt 0 3 e
2
6、分析:作出 y x , y x 及 y 2x的图如右
y y=2x
y 2x x 2 x 0 B(2,4)
解方程组 得 2
y x y 4 y 0
y=x
y x x 1 x 0
解方程组 得 A(1,1)
y x
2
y 1 y 0 o x 1 2
所求面积 s
1
0 (2x x)dx
2
1 (2x x
2 )dx
1 2 2
0 xdx 1 (2x x )dx
1 2 1 1
x | (x2 x3) |2 0 1
2 3
7
6
2u
7、分析:令 e
t 1 u 2,则 t ln 1 u ,dt du
1 u 2
当 t 2ln 2时,u 3
当 t x时,u e
x 1
2ln 2 dt 3 2udu 3
∴ 2arctgu x x t ex 1e 1 1 u 2 u e 1
2 arctg e
x 1
3 6
从而 x ln 2
x
2a
8、分析:左端 lim 1 2a e
x x a
2
右端 2x e
2x d 2x 2x
2de 2x
a a
2 x2e 2x 2x 2xe dx
a a
2 2a
2a e 2 xde
2x
a
2
2a e 2a 2 xe 2x e 2x dx
a a
2a 2 2a 1 e 2a
2a 2 2a 2a ∴ 2a 1 e e
解之a 0或a 1。
B 组
9、分析: 2(1)设切点 A(x0,x0 ),切线斜率为 k y x x 2x0 0 ,
切线方程为 y x20 2x0(x x0) ,
x
令 y 0,得 x 0 .
2
x0 x0
s 2 x2dx [x2
1 1
x (2x0x x
2
0 )]dx x
3
0 ,
0 0
2 12 12
解得 x0 1, 切点 A 的坐标为 (1,1);
(2)将 A(1,1) 代入切线方程,得 y 1 2(x 1) ,
整理,得 y 2x 1.
即所求切线方程为 y 2x 1
答案:B
10、分析:设直线 OP 的方程为 y=kx, P 点的坐标为(x,y),
x 2
则 (kx-x2)dx= (x2-kx)dx, 0 x
1 1 x 1 1 2
即( kx2- x3) =( x3- kx2) ,
2 3 0 3 2 x
1 1 8 1 1
解得 kx2- x3= -2k-( x3- kx2),
2 3 3 3 2
4 4 4 16
解得 k= ,即直线 OP 的方程为 y= x,所以点 P 的坐标为( , ).
3 3 3 9
11、分析:(1)0≤a≤1时,
1
f(a)= |x2-a2|dx 0
a 1
= (a2-x2)dx+ (x2-a2)dx 0 a
1 a x3 1
=(a2x- x3) +( -a2x)
3 0 3 a
1 1 a3
=a3- a3-0+0+ -a2- +a3
3 3 3
4 1
= a3-a2+ .
3 3
当 a>1 时,
1
f(a)= (a2-x2)dx 0
1 1
=(a2x- x3)
3 0
1
=a2- .
3
4 3 2 1
a a (0≤ a≤1), 3 3
∴f(a)=
2 1a (a>1).
3
1 1 2
(2)当 a>1 时,由于 a2- 在[1,+∞)上是增函数,故 f(a)在[1,+∞)上的最小值是 f(1)=1- = .
3 3 3
当 a∈[0,1]时,f′(a)=4a2-2a=2a(2a-1),
1
由 f′(a)>0 知:a> 或 a<0,
2
1 1
故在[0, ]上递减,在[ ,1]上递增.
2 2
1 1
因此在[0,1]上,f(a)的最小值为 f( )= .
2 4
1
综上可知,f(x)在[0,+∞)上的最小值为 .
4
一、知识方法拓展
1、曲边梯形的定义
我们把由直线 x a, x b(a b), y 0和曲线 y f (x)所围成的图形称为曲边梯形。
2、曲边梯形的面积的求法
分割→近似代替(以直代曲)→求和→取极限
3、定积分的概念
一般地,设函数 f (x) 在区间[a,b]上连续,用分点
a = x0 < x1 < x2 < ...< xi-1 < xi < ...< xn = b
b - a
将区间[a,b]等分成 n 个小区间,每个小区间长度为Dx ( D = ),在每个小区间[xi-1 , xi ]上任取一x n
n n b a
点 xi (i = 1,2,...,n),作和式: S n f (xi ) x f ( i )
i 1 i 1 n
如果Dx 无限接近于0 (亦即n )时,上述和式 Sn 无限趋近于常数 S ,那么称该常数 S 为函数
b
f (x) 在区间[a,b]上的定积分。记为: S f (x)dx, a
其中 是积分号,b 是积分上限, a 是积分下限, f (x) 是被积函数, x 是积分变量,[a,b]是积分区
间, f (x)dx是被积式。
b
说明:(1)定积分 f (x)dx 是一个常数,可以是正数,也可以是负数,也可以是零,即 Sn 无限趋近a
b
的常数 S ( n 时)记为 f (x)dx ,而不是 Sn . a
(2)用定义求定积分的一般方法是:①分割: n 等分区间[a,b ];②近似代替:取点 i xi 1 , xi ;③
n b a b n b a
求和: f ( i );④取极限: f (x)dx lim f i n a n i 1 i 1 n
4、定积分的性质
根据定积分的定义,不难得出定积分的如下性质:
b b
性质 1 kf (x)dx k f (x)dx(k为常数) ; a a
b b b
性质 2 [ f1(x) f2(x)]dx f1(x)dx f2(x)dx ; a a a
b c b
性质 3 f (x)dx f (x)dx f (x)dx (其中a c b) a a c
5、定积分的几何意义
b
(1)从几何上看,如果在区间[a,b]上函数 f (x) 连续且恒有 f (x) 0,那么定积分 f x dx表示由直a
线 x a, x b(a b), y 0和曲线 y f (x)所围成的曲边梯形(如图中的阴影部分)的面积。
b
(2)从几何上看,如果在区间[a,b]上函数 f (x) 连续且恒有 f (x) 0,那么定积分 f x dx表示由直a
线 x a, x b(a b), y 0和曲线 y f (x)所围成的曲边梯形(如图中的阴影部分)的面积的相反数。
(3)从几何上看,如果在区间[a,b]上函数 f (x) 连续,且函数 y f (x) 的图像有一部分在 x 轴上方,有
b
一部分在 x 轴下方,那么定积分 f x dx表示 x 轴上方的曲边梯形的面积减去下方的曲边梯形的面积。 a
b
(4)图中阴影部分的面积 S= [ f1(x) f2(x)]dx a
6、微积分基本定理
b
1
一般地,如果 f (x) 是区间[a,b]上的连续函数,并且F (x) f (x),那么 f (x)dx F(b) F(a) ,a
b
这个结论叫做微积分基本定理,又叫牛顿—莱布尼茨公式。为了方便,我们常把F(b) F(a)记成F (x) a ,
b
f (x)dx F(x) b即 a F(b) F(a) 。 a
1
计算定积分的关键是找到满足 F (x) f (x)的函数F(x)。
7、常见定积分公式
b n 1 n 1 b
(1) a x dx x |a (n 1)n 1
b b
(2) a cdx cx |a (C 为常数)
b
(3) a sin xdx cos x |
b
a
b
(4) a cos xdx sin x |
b
a
b 1
(5) a dx ln x |
b
a (b a 0)
x
b x x b
(6) a e dx e |a
x
b x a b
(7) a a dx |a (a 0且a 1) ln a
二、热身练习
【例 1】计算下列各式:
6
2
(1) (x 1)dx =_____________; 0
分析:78
2
(2) (sin x 2)dx ___________; 2
分析: 8
e e
(3) (2
x )dx =_____________;
1 x
2e 2
分析: e
ln 2 ln 2
x
(4) 2 sin
2 dx =____________; 0
2
1
分析:
4 2
x2 (0 x 1)
2
【例 2】已知 f (x) ,则 0 f (x)dx =__________;
2 x (1 x 2)
分析:
【例 3】给出如下命题:
a b
③ dx b dt b a ( a,b 为常数且a b ); a
0 1
② 2 2
π
1 x dx 1 x dx ; 1 0 4
③曲线 y sin x , x [0,2π],与直线 y 0围成的两个封闭区域的面积之和为 2.
其中真命题的个数为( )
A.0 B.1 C. 2 D.3
分析:B
3
2
【例 4】 x 4 dx 等于( ) 0
21 22 23 25
A. B. C. D.
3 3 3 3
分析:C
三、真题讲解
【例 】已知 f (x) x (12t 4a)dt, F (a) 11 a 0[ f (x) 3a
2 ]dx ,求函数F (a) 的最小值.
分析: f (x) x a (12t 4a)dt
(6t2 4at) |x 6x2 a 4ax (6x
2 4a2) 6x2 4a 2a2
F (a) 1 0[ f (x) 3a
2 ] 1 (6x2 0 4ax a
2 )dx
3 2 2 1 3 2 2
(2x 2ax a x) |0 2.1x 2a.1 a .1
2 2
a 2a 2 (a 1) 1 1
当a 1时, F (a) 最小=1 当a 1时,F (a) 最小=1
【例 2】求在[0,2 ]上,由 x 轴及正弦曲线 y sin x 围成的图形的面积.
分析:作出 y sin x 在[0,2 ]上的图象如右 y
y sin x 与 x 轴交于 0、 、2 ,所
x
0 Л
s
2Л
求积 0 sin xdx |
2
sin xdx | ( cos x) |
( cos x) |2 0 4
【例 3】若 y= ,则 y 的最大值是( )
7
A.1 B.2 C.- D.0
2
分析:y= =
1 x 1 5
=(-cost- cos2t)| =-cosx- cos2x+
4 0 4 4
1 5 1 3
=-cosx- (2cos2x-1)+ =- cos2x-cosx+
4 4 2 2
1
=- (cosx+1)2+2≤2.
2
答案:B
17
【例 4】若 f(x)是一次函数,且 , ,那么 dx 的值是________.
6
1 1 1 1
分析:∵f(x)是一次函数,∴设 f(x)=ax+b(a≠0),由 (ax+b)dx=5 得( ax2+bx) = a+b=5, 0 2 0 2
①
1 17 1 17
由 xf(x)dx= 得 (ax2+bx)dx= ,即 0 6 0 6
1 1 1 17 1 1 17
( ax3+ bx2) = ,∴ a+ b= , ②
3 2 0 6 3 2 6
解①②得 a=4,b=3,∴f(x)=4x+3,
2 f(x) 2 4x+3 2 3
于是 dx= dx= (4+ )dx 1 x 1 x 1 x
2
=(4x+3lnx) =8+3ln2-4=4+3ln2.
1
答案:4+3ln2
【例 5】设 f (x) x ln x ,
(1)求 f (x);
1 b
(2)设0 a b,求常数 C,使得 ln x C dx取得最小值; b a a
(3)记(2)中的最小值为m ,证明: . a,b ma,b ln 2
1
分析:(1) f (x) = ln x + x = ln x +1
x
(2)若C ≤ln a ,则 ln x - C = ln x - C,显然,当C = ln a , ln x - C 取最小;若C ≥ln b,
则 ln x - C = C - ln x,当C = ln b,C - ln x 取最小
故不妨设 ln a ≤C ≤ln b
1 b
ln x C dx=
b a a
由(1)可知,
因
1 b
所以 ln x C dx
b a a
记 g(C) = a ln a + b ln b + 2ec - (a + b)C - (a + b)
c a + b
令 g ' (C) = 2e - (a+b) = 0,得C = ln
2
a + b 1 b
即C = ln , ln x C dx取最小值 2 b a a
a + b 1 b
(3)将C = ln 代入 ln x C dx 2 b a a
的右边,
1 a + b a + b
ma,b = [a ln a + b ln b - (a + b) ln ] < ln 2 a ln a + b ln b - (a + b) ln < (b - a) ln 2b - a 2 2
a ln a + b ln b + 2a ln 2 < (a + b) ln(a + b) 2a ln 2 < a ln(a + b) - a ln a + b ln(a + b) - blnb
b a
2a ln 2 < a ln(1+ ) + b ln(1+ )
a b
b b a
由于0 a b,故 +1 > 2,所以a ln(1+ ) > a ln 2,即只需证明b ln(1+ ) > a ln 2
a a b
a b a
a ln 2 < b ln(1+ ) ln 2 < ln(1+ )
b a b
a b a ln(1+ m)
1
令 = m∈(0,1),则 ln(1+ ) = = ln(1+ m)m
b a b m
1 1 1
函数 ln(1+ m) m 单调递减且m∈(0,1),所以 ln(1+ m)m > ln(1+1)1 = ln 2,得证
四、重点总结
1、能快速反应出常见的微分公式
2、利用牛顿-莱布尼兹公式计算
3、利用微积分求曲边梯形面积
五、强化训练
A 组
x 1, x 1
2
1、设 f x 1 ,求 f x dx。 x 2 0 , x 1
2
1 2
2 1 2 1 1 1 8
分析: f x dx x 1 dx x
2dx 2 x x x
3
0 0 1 2 2 6 1 30
2、已知 f(x)为偶函数且 ,则 等于( )
A.0 B.4 C.8 D.16
0 6
分析:原式= f(x)dx+ 6 f(x)dx, 0
∵原函数为偶函数,
∴在 y 轴两侧的图象对称,
∴对应的面积相等,即 8×2=16.
答案:D
3、函数 y=-x2+2x+1 与 y=1 相交形成一个闭合,则该闭合图形的面积
是( )
4
A.1 B. C. 3 D.2
3
分析:函数 y=-x2+2x+1 与 y=1 的两个交点为(0,1)和(2,1),所以闭合图
2 2 4
形的面积等于 (-x2+2x+1-1)dx=0 (-x
2+2x)dx= .
0 3
4
4、已知函数 y=x2与 y=kx(k>0)的图象所围成的阴影部分(如图所示)的面积为 ,则 k=________.
3
k kx2 x3 k k3 4
分析:直线方程与抛物线方程联立先求出积分区间为[0,k],再由 (kx-x2)dx=( - )y=x=2 =0 2 3 0 6 3
求得 k=2.
答案:2
1 x
2 , x 0 3
5、设 f x ,求 f x 2 dx 。
e x , x 0
1
分析:令 x 2 t ,则
3 1 0 1 7 1
f x 2 dx f t dt 1 t
2 dt t e dt 1 1 1 0 3 e
6、求曲线 y x2 , y x 及 y 2x所围成的平面图形的面积.
分析:作出 y x2 , y x 及 y 2x的图如右
y 2x x 2 x 0 B(2,4)
解方程组 得
y x
2
y 4 y 0
y=x
y x x 1 x 0
解方程组 得 A(1,1) 2
y x y 1 y 0 o x 1 2
1
所求面积 s 0 (2x x)dx
2
1 (2x x
2 )dx
1 2 2
0 xdx 1 (2x x )dx
1 1
x2 |1 (x2 x3) |2 0 1
2 3
7
6
2 ln 2 dt
7、若 ,求 x 。 x
e t 1 6
t 2 2u
分析:令 e 1 u ,则 t ln 1 u ,dt du
1 u 2
当 t 2ln 2时,u 3
x
当 t x时,u e 1
2ln 2 dt 3 2udu 3
∴ x t 2arctgu x ex 1 2 e 1e 1 1 u u
2 x arctg e 1
3 6
从而 x ln 2
x
x a
、已知 lim 4x2e 2x8 dx ,求常数 a 。 x x a a
x
2a
分析:左端 lim 1 2a e
x x a
右端 2x2e 2x d 2x 2x2de 2x a a
2 x2e 2x 2xe 2x dx
a a
2a2e 2a 2x 2 xde a
2a2e 2a 2 xe 2x e 2x dx
a a
2a 2 2a 1 e 2a
2 2a 2a
∴ 2a 2a 1 e e
解之a 0或a 1。
B 组
y = x2
1
9、在曲线 (x ≥0)上某一点 A 处作一切线使之与曲线以及 x 轴所围成图形的面积为 ,试求:
12
(1)切点 A 的坐标;
(2)过切点 A 的切线方程.
分析:(1)设切点 A(x 2 ,切线斜率为 k y 0,x0 ) x x 2x0 , 0
切线方程为 y x20 2x0(x x , 0)
x
令 y 0,得 x 0 .
2
x0 x
2 0 1 1
s 2 x dx x [x
2 (2x x x2 )]dx x30 0 0 ,
0 0
2 12 12
解得 x0 1, 切点 A 的坐标为 (1,1);
(2)将 A(1,1) 代入切线方程,得 y 1 2(x 1) ,
整理,得 y 2x 1.
即所求切线方程为 y 2x 1
答案:B
10、如图,设点 P 从原点沿曲线 y=x2向点 A(2,4)移动,记直线 OP、曲线 y=x2 及直线 x=2 所围成的
面积分别记为 S1,S2,若 S1=S2,求点 P 的坐标.
分析:设直线 OP 的方程为 y=kx, P 点的坐标为(x,y),
x 2
则 (kx-x2)dx= (x2-kx)dx, 0 x
1 1 x 1 1 2
即( kx2- x3) =( x3- kx2) ,
2 3 0 3 2 x
1 1 8 1 1
解得 kx2- x3= -2k-( x3- kx2),
2 3 3 3 2
4 4 4 16
解得 k= ,即直线 OP 的方程为 y= x,所以点 P 的坐标为( , ).
3 3 3 9
11、设 f(x)=
(1)当 0≤a≤1与 a>1 时,分别求 f(a);
(2)当 a≥0时,求 f(a)的最小值.
分析:(1)0≤a≤1时,
1
f(a)= |x2-a2|dx 0
a 1
= (a2-x2)dx+ (x2-a2)dx 0 a
1 a x3 1
=(a2x- x3) +( -a2x)
3 0 3 a
1 1 a3
=a3- a3-0+0+ -a2- +a3
3 3 3
4 1
= a3-a2+ .
3 3
当 a>1 时,
1
f(a)= (a2-x2)dx 0
1 1
=(a2x- x3)
3 0
1
=a2- .
3
4 3 2 1
a a (0≤ a≤1), 3 3
∴f(a)=
2 1a (a>1).
3
1 1 2
(2)当 a>1 时,由于 a2- 在[1,+∞)上是增函数,故 f(a)在[1,+∞)上的最小值是 f(1)=1- = .
3 3 3
当 a∈[0,1]时,f′(a)=4a2-2a=2a(2a-1),
1
由 f′(a)>0 知:a> 或 a<0,
2
1 1
故在[0, ]上递减,在[ ,1]上递增.
2 2
1 1
因此在[0,1]上,f(a)的最小值为 f( )= .
2 4
1
综上可知,f(x)在[0,+∞)上的最小值为 .
4
六、参考答案
A 组
1 2
2 1 2 1 1 1 8
1、分析: f
x dx x 1 dx x
2
dx x
2 x x
3
0 0 1 2 2 6 1 30
0 6
2、分析:原式= f(x)dx+ f(x)dx, 6 0
∵原函数为偶函数,
∴在 y 轴两侧的图象对称,
∴对应的面积相等,即 8×2=16.
答案:D
2
3、分析:函数 y=-x2+2x+1 与 y=1 的两个交点为(0,1)和(2,1),所以闭合图形的面积等于 (-x20
2 4
+2x+1-1)dx= (-x2+2x)dx= . 0 3
k kx2 x3 k k3
4、分析:直线方程与抛物线方程联立先求出积分区间为[0,k],再由 (kx-x2)dx=( -0 2 y= )3x20
=
6
4
= 求得 k=2.
3
答案:2
5、分析:令 x 2 t ,则
3 1 0 1 7 1
f x 2 dx f t dt 1 t
2
dt
t
1 1 1 e dt 0 3 e
2
6、分析:作出 y x , y x 及 y 2x的图如右
y y=2x
y 2x x 2 x 0 B(2,4)
解方程组 得 2
y x y 4 y 0
y=x
y x x 1 x 0
解方程组 得 A(1,1)
y x
2
y 1 y 0 o x 1 2
所求面积 s
1
0 (2x x)dx
2
1 (2x x
2 )dx
1 2 2
0 xdx 1 (2x x )dx
1 2 1 1
x | (x2 x3) |2 0 1
2 3
7
6
2u
7、分析:令 e
t 1 u 2,则 t ln 1 u ,dt du
1 u 2
当 t 2ln 2时,u 3
当 t x时,u e
x 1
2ln 2 dt 3 2udu 3
∴ 2arctgu x x t ex 1e 1 1 u 2 u e 1
2 arctg e
x 1
3 6
从而 x ln 2
x
2a
8、分析:左端 lim 1 2a e
x x a
2
右端 2x e
2x d 2x 2x
2de 2x
a a
2 x2e 2x 2x 2xe dx
a a
2 2a
2a e 2 xde
2x
a
2
2a e 2a 2 xe 2x e 2x dx
a a
2a 2 2a 1 e 2a
2a 2 2a 2a ∴ 2a 1 e e
解之a 0或a 1。
B 组
9、分析: 2(1)设切点 A(x0,x0 ),切线斜率为 k y x x 2x0 0 ,
切线方程为 y x20 2x0(x x0) ,
x
令 y 0,得 x 0 .
2
x0 x0
s 2 x2dx [x2
1 1
x (2x0x x
2
0 )]dx x
3
0 ,
0 0
2 12 12
解得 x0 1, 切点 A 的坐标为 (1,1);
(2)将 A(1,1) 代入切线方程,得 y 1 2(x 1) ,
整理,得 y 2x 1.
即所求切线方程为 y 2x 1
答案:B
10、分析:设直线 OP 的方程为 y=kx, P 点的坐标为(x,y),
x 2
则 (kx-x2)dx= (x2-kx)dx, 0 x
1 1 x 1 1 2
即( kx2- x3) =( x3- kx2) ,
2 3 0 3 2 x
1 1 8 1 1
解得 kx2- x3= -2k-( x3- kx2),
2 3 3 3 2
4 4 4 16
解得 k= ,即直线 OP 的方程为 y= x,所以点 P 的坐标为( , ).
3 3 3 9
11、分析:(1)0≤a≤1时,
1
f(a)= |x2-a2|dx 0
a 1
= (a2-x2)dx+ (x2-a2)dx 0 a
1 a x3 1
=(a2x- x3) +( -a2x)
3 0 3 a
1 1 a3
=a3- a3-0+0+ -a2- +a3
3 3 3
4 1
= a3-a2+ .
3 3
当 a>1 时,
1
f(a)= (a2-x2)dx 0
1 1
=(a2x- x3)
3 0
1
=a2- .
3
4 3 2 1
a a (0≤ a≤1), 3 3
∴f(a)=
2 1a (a>1).
3
1 1 2
(2)当 a>1 时,由于 a2- 在[1,+∞)上是增函数,故 f(a)在[1,+∞)上的最小值是 f(1)=1- = .
3 3 3
当 a∈[0,1]时,f′(a)=4a2-2a=2a(2a-1),
1
由 f′(a)>0 知:a> 或 a<0,
2
1 1
故在[0, ]上递减,在[ ,1]上递增.
2 2
1 1
因此在[0,1]上,f(a)的最小值为 f( )= .
2 4
1
综上可知,f(x)在[0,+∞)上的最小值为 .
4
同课章节目录
