数学八年级人教新课标12.3等腰三角形(第1课时)课件
文档属性
| 名称 | 数学八年级人教新课标12.3等腰三角形(第1课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 680.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-10 16:25:54 | ||
图片预览


文档简介
(共18张PPT)
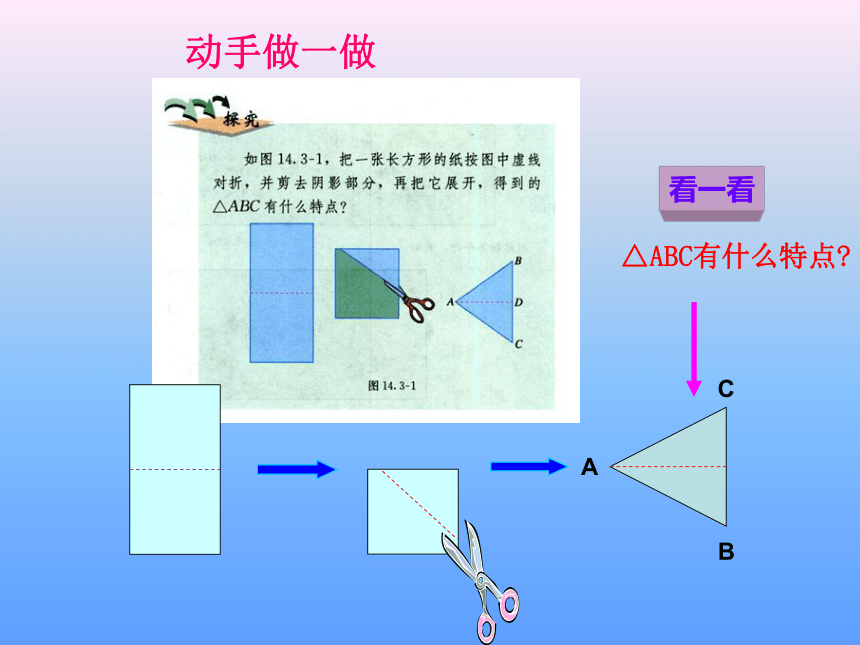
动手做一做
A
C
B
△ABC有什么特点
看一看
底角
腰
腰
C
底边
顶角
底角
A
B
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,
腰和底边的夹角叫做底角.
两腰的夹角叫做顶角,
把剪出的等腰三角形ABC沿折痕对折,
找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
是
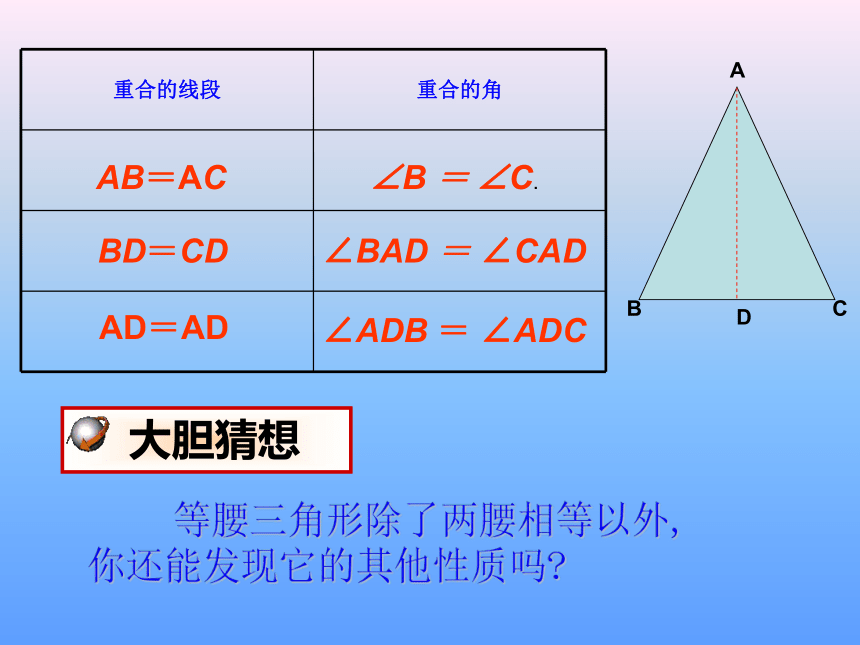
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗
大胆猜想
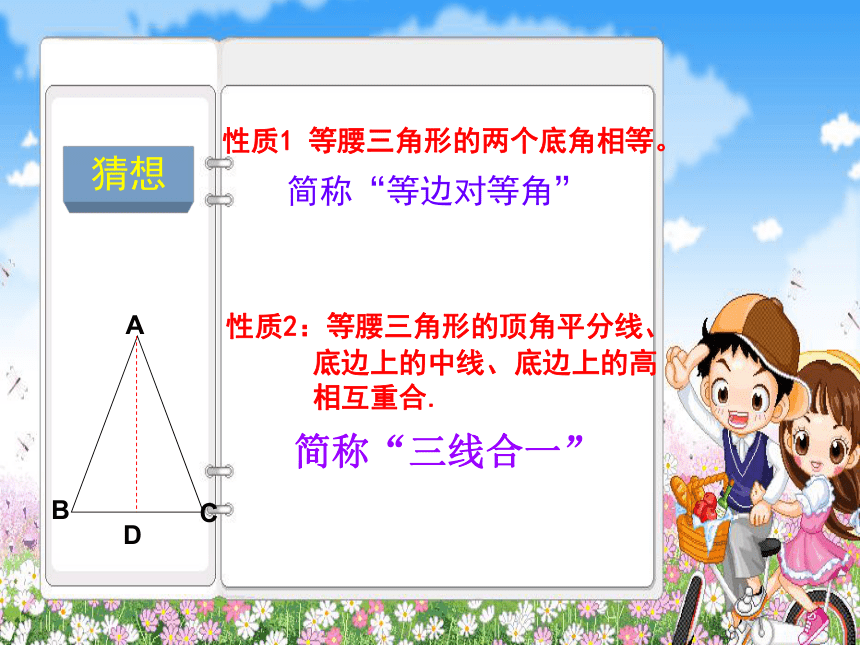
性质1 等腰三角形的两个底角相等。
简称“等边对等角”
A
B
C
D
猜想
性质2:等腰三角形的顶角平分线、
底边上的中线、底边上的高
相互重合.
简称“三线合一”
如何证明我们猜想的两个性质呢?
性质1 等腰三角形的两个底角相等。
性质2:等腰三角形的顶角平分线、
底边上的中线、底边上的高
相互重合.
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
想一想:
刚才的证明中,从△ABD≌ △ACD, 除了能得到∠B=∠C , 你还能发现什么
A
B
D
C
BD=CD
∠BAD = ∠CAD
∠ADB =∠ADC =90°
AD是底边上中线
AD是顶角的平分线
AD是底边上的高
由此可证明性质2
下面证明性质2的方法中分别是怎样做辅助线的
(1) ------------- (2)----------------
BD=CD
∠BAD=∠CAD
BD=CD
AD⊥BC
(1) ------------- (2)----------------
AD⊥BC
∴
∵
∴
∵
A
B
D
C
△ABC中,AB=AC,----------------------
∠BAD=∠CAD
AD⊥BC
△ABC中,AB=AC,----------------------
(方法三)
BD=CD
∠BAD=∠CAD
△ABC中,AB=AC,----------------------
(1) ------------- (2)----------------
∴
∵
(方法一)
(方法二)
抢答!!
(作顶角的平分线)
(作底边上中线)
(作底边上的高)
例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=______,∠A= _____ (_______________)
设∠A=x,则∠BDC= ____+ ∠ABD=____,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=_____,
解得x=_____,
在△ABC中, ∠A=36°,∠ABC=∠C=_____
x
⌒
2x
⌒
2x
⌒
⌒
2x
∠BDC
∠ABD
等边对等角
∠A
2x
180°
36°
72°
你的细心+你的耐心=成功!
1.等腰三角形的顶角为80°,它的另外两个角
为______________;
2.等腰三角形一个底角为30°,它的另外两个角为
_________________;
⒊等腰三角形一个角为70°,它的另外两个角为
______ _____________________。
50°, 50°
30°, 120°
70°, 40°
或55°, 55°
某地地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线强经过三角尺的直角顶点,同学们确信房梁是水平的.他们的判断对吗 为什么
A
C
B
O
等腰三角形“三线合一”
的性质.
谈谈你的收获!
轴对称图形
两个底角相等,
简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,
简称“三线合 一”
作业设计
必做题:P56习题 3、4
思考题:如果一个三角形中有两个角
相等,那么这个三角是等腰
三角形吗?为什么?
动手做一做
A
C
B
△ABC有什么特点
看一看
底角
腰
腰
C
底边
顶角
底角
A
B
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,
腰和底边的夹角叫做底角.
两腰的夹角叫做顶角,
把剪出的等腰三角形ABC沿折痕对折,
找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
是
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗
大胆猜想
性质1 等腰三角形的两个底角相等。
简称“等边对等角”
A
B
C
D
猜想
性质2:等腰三角形的顶角平分线、
底边上的中线、底边上的高
相互重合.
简称“三线合一”
如何证明我们猜想的两个性质呢?
性质1 等腰三角形的两个底角相等。
性质2:等腰三角形的顶角平分线、
底边上的中线、底边上的高
相互重合.
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
想一想:
刚才的证明中,从△ABD≌ △ACD, 除了能得到∠B=∠C , 你还能发现什么
A
B
D
C
BD=CD
∠BAD = ∠CAD
∠ADB =∠ADC =90°
AD是底边上中线
AD是顶角的平分线
AD是底边上的高
由此可证明性质2
下面证明性质2的方法中分别是怎样做辅助线的
(1) ------------- (2)----------------
BD=CD
∠BAD=∠CAD
BD=CD
AD⊥BC
(1) ------------- (2)----------------
AD⊥BC
∴
∵
∴
∵
A
B
D
C
△ABC中,AB=AC,----------------------
∠BAD=∠CAD
AD⊥BC
△ABC中,AB=AC,----------------------
(方法三)
BD=CD
∠BAD=∠CAD
△ABC中,AB=AC,----------------------
(1) ------------- (2)----------------
∴
∵
(方法一)
(方法二)
抢答!!
(作顶角的平分线)
(作底边上中线)
(作底边上的高)
例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=______,∠A= _____ (_______________)
设∠A=x,则∠BDC= ____+ ∠ABD=____,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=_____,
解得x=_____,
在△ABC中, ∠A=36°,∠ABC=∠C=_____
x
⌒
2x
⌒
2x
⌒
⌒
2x
∠BDC
∠ABD
等边对等角
∠A
2x
180°
36°
72°
你的细心+你的耐心=成功!
1.等腰三角形的顶角为80°,它的另外两个角
为______________;
2.等腰三角形一个底角为30°,它的另外两个角为
_________________;
⒊等腰三角形一个角为70°,它的另外两个角为
______ _____________________。
50°, 50°
30°, 120°
70°, 40°
或55°, 55°
某地地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线强经过三角尺的直角顶点,同学们确信房梁是水平的.他们的判断对吗 为什么
A
C
B
O
等腰三角形“三线合一”
的性质.
谈谈你的收获!
轴对称图形
两个底角相等,
简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,
简称“三线合 一”
作业设计
必做题:P56习题 3、4
思考题:如果一个三角形中有两个角
相等,那么这个三角是等腰
三角形吗?为什么?
