数学八年级人教版:作轴对称图形
文档属性
| 名称 | 数学八年级人教版:作轴对称图形 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-10 16:25:54 | ||
图片预览








文档简介
(共34张PPT)
12.2.1作轴对称图形
回顾旧知识
1、如果一个图形沿一条直线折叠,直线两旁的
部分能够互相重合,这个图形就叫做轴对称图形。
2、如果两个图形关于某条直线对称,那么对
称轴是任何一对对应点所连线段的垂直平分线。
欣赏中国民间的剪纸艺术
欣赏中国民间的剪纸艺术
欣赏中国民间的剪纸艺术
动手试一试
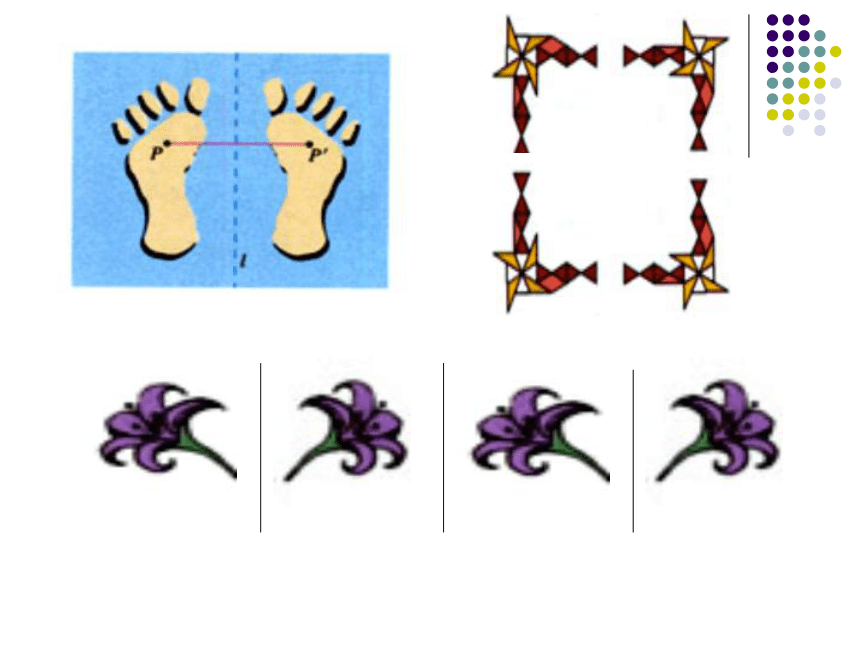
在一 张半透明的纸的左边画一只左手印,再把这张纸对折后描图,打开对折的纸。就能得到相应的右手印。
动脑想一 想
左手印和右手印有什么关系?
成轴对称。
对称轴是
折痕所在的直线,即直线
图中的 与 m 是什么关系?
m。
m
.
.
p
由一个平面图形得到它的轴对称图形叫做轴对称变换
.
.
.
.
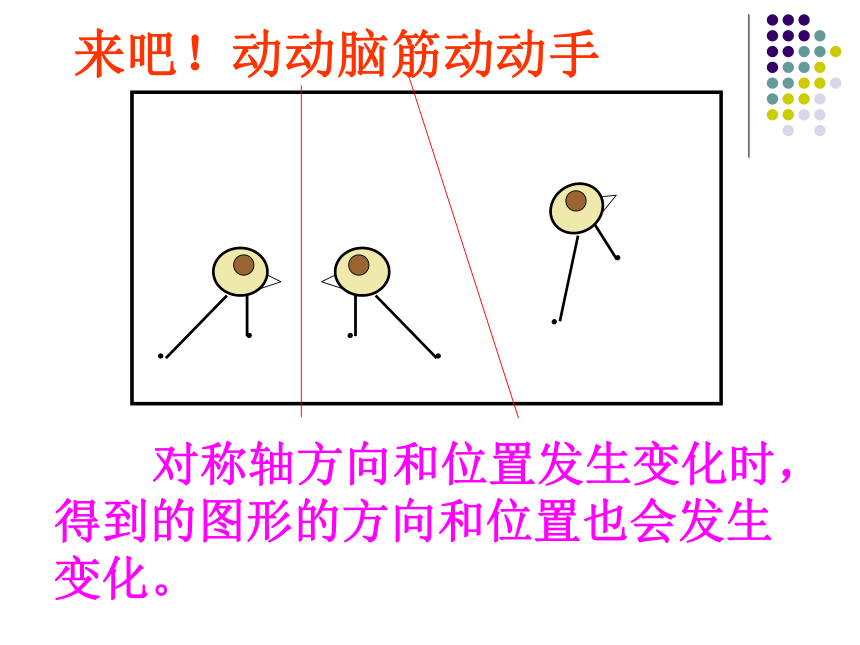
对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化。
来吧!动动脑筋动动手
.
.
.
.
.
.
.
.
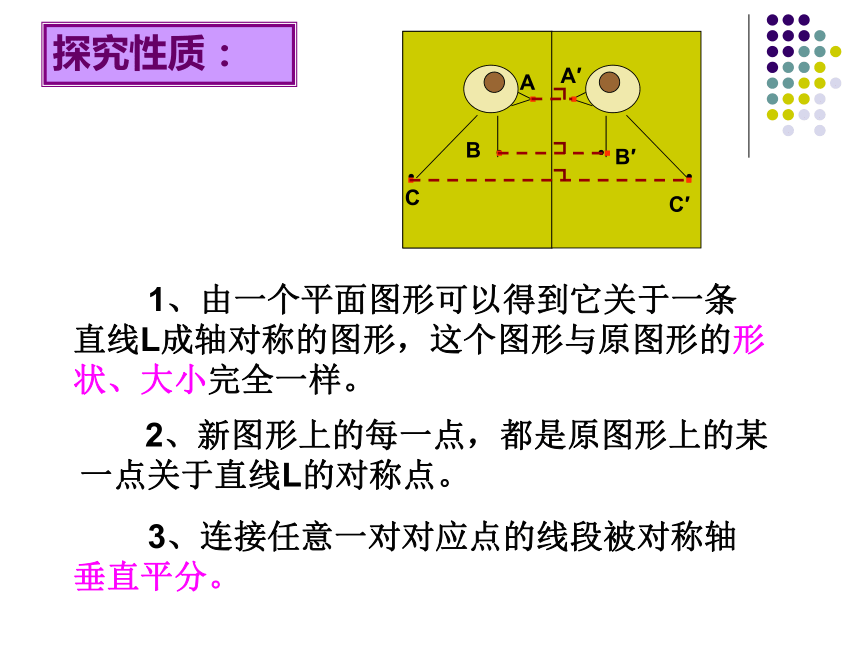
探究性质:
1、由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全一样。
2、新图形上的每一点,都是原图形上的某一点关于直线L的对称点。
3、连接任意一对对应点的线段被对称轴垂直平分。
·
·
·
·
·
·
A
A′
B
B′
C
C′
┓
┓
┓
讨论:
如果有一个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?
已知直线 和一个点A,作出点A与A′关于直线 对称的图形。
A
A'
∴ 点A′即为所求
M
l
┓
O
基础一
l
l
A
B
已知直线L和线段AB,作出线段AB与A′B′关于直线 L对称的图形。
A'
B'
l
M
N
┓
┓
O
P
基础二
∴线段A′B′即为所求
例1
如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
┐
┐
┐
l
作法:
(1)过点A作直线l的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点。
(4)连接A′B′、B′C′、C′A′,得到△A′B′C′即为所求。
O
P
M
(2)过点B作直线l的垂线,垂足为点P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点。
(3)过点C作直线l的垂线,垂足为点M,在垂线上截取MC′=MC,点C′就是点C关于直线l的对称点。
变式训练
请画出⊿ABC关于直线 的对称⊿ A’B’C’.
A
B
C
归纳
1、找特征点
2、作垂线
3、截取等长
4、依次连线
作图步骤
归纳
几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形
对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,再连接对称点,就可以得到原图形的轴对称图形
练习 1、如图,把下列图形补成关于直线L的对称图形。
如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴。
整个图案是个什么形状?请准确地画出它的另一半。
巩固提高
B
A
C
D
E
F
G
H
实际图形和印章中的像可以看成上图那样的成轴对称关系。
轴对称变换后的像
原来的像
China
Beijing
2008
Olympic
轴对称变换前后的 图形是一对“好朋友”,在一次活动中他们走散了,请同学们帮助他们找回自己的“好朋友”。
用两个圆、两个三角形、两条平行线段可以构造出许多独特而有意义的轴对称图形(如下图),请你也仿照构思一个图案,别忘了加上一两句贴切的解说词哦.
活动
两盏电灯
图片欣赏
图片欣赏
图片欣赏
图片欣赏
图片欣赏
(1)轴对称变换的定义
(2)轴对称变换的性质
今天你学到了什么
(4)轴对称变换在生活中的应用
(3)利用轴对称变换的性质作图
课本45-46页习题第1题、第5题。
再见
12.2.1作轴对称图形
回顾旧知识
1、如果一个图形沿一条直线折叠,直线两旁的
部分能够互相重合,这个图形就叫做轴对称图形。
2、如果两个图形关于某条直线对称,那么对
称轴是任何一对对应点所连线段的垂直平分线。
欣赏中国民间的剪纸艺术
欣赏中国民间的剪纸艺术
欣赏中国民间的剪纸艺术
动手试一试
在一 张半透明的纸的左边画一只左手印,再把这张纸对折后描图,打开对折的纸。就能得到相应的右手印。
动脑想一 想
左手印和右手印有什么关系?
成轴对称。
对称轴是
折痕所在的直线,即直线
图中的 与 m 是什么关系?
m。
m
.
.
p
由一个平面图形得到它的轴对称图形叫做轴对称变换
.
.
.
.
对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化。
来吧!动动脑筋动动手
.
.
.
.
.
.
.
.
探究性质:
1、由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全一样。
2、新图形上的每一点,都是原图形上的某一点关于直线L的对称点。
3、连接任意一对对应点的线段被对称轴垂直平分。
·
·
·
·
·
·
A
A′
B
B′
C
C′
┓
┓
┓
讨论:
如果有一个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?
已知直线 和一个点A,作出点A与A′关于直线 对称的图形。
A
A'
∴ 点A′即为所求
M
l
┓
O
基础一
l
l
A
B
已知直线L和线段AB,作出线段AB与A′B′关于直线 L对称的图形。
A'
B'
l
M
N
┓
┓
O
P
基础二
∴线段A′B′即为所求
例1
如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
┐
┐
┐
l
作法:
(1)过点A作直线l的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点。
(4)连接A′B′、B′C′、C′A′,得到△A′B′C′即为所求。
O
P
M
(2)过点B作直线l的垂线,垂足为点P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点。
(3)过点C作直线l的垂线,垂足为点M,在垂线上截取MC′=MC,点C′就是点C关于直线l的对称点。
变式训练
请画出⊿ABC关于直线 的对称⊿ A’B’C’.
A
B
C
归纳
1、找特征点
2、作垂线
3、截取等长
4、依次连线
作图步骤
归纳
几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形
对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,再连接对称点,就可以得到原图形的轴对称图形
练习 1、如图,把下列图形补成关于直线L的对称图形。
如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴。
整个图案是个什么形状?请准确地画出它的另一半。
巩固提高
B
A
C
D
E
F
G
H
实际图形和印章中的像可以看成上图那样的成轴对称关系。
轴对称变换后的像
原来的像
China
Beijing
2008
Olympic
轴对称变换前后的 图形是一对“好朋友”,在一次活动中他们走散了,请同学们帮助他们找回自己的“好朋友”。
用两个圆、两个三角形、两条平行线段可以构造出许多独特而有意义的轴对称图形(如下图),请你也仿照构思一个图案,别忘了加上一两句贴切的解说词哦.
活动
两盏电灯
图片欣赏
图片欣赏
图片欣赏
图片欣赏
图片欣赏
(1)轴对称变换的定义
(2)轴对称变换的性质
今天你学到了什么
(4)轴对称变换在生活中的应用
(3)利用轴对称变换的性质作图
课本45-46页习题第1题、第5题。
再见
