人教版数学九年级上期第二十三章旋转——证明题基础篇(含解析)
文档属性
| 名称 | 人教版数学九年级上期第二十三章旋转——证明题基础篇(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 206.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 14:12:06 | ||
图片预览


文档简介
人教版数学九年级上期
第二十三章旋转——证明题基础篇1
如图,ABO与CDO关于点O成中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.
在△ABC和△ADE中,点E在BC边上,∠EAC=∠DAB,∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)将△ABC绕着点A旋转得到△ADE,如果∠AEC=70°,求∠BAD的度数.
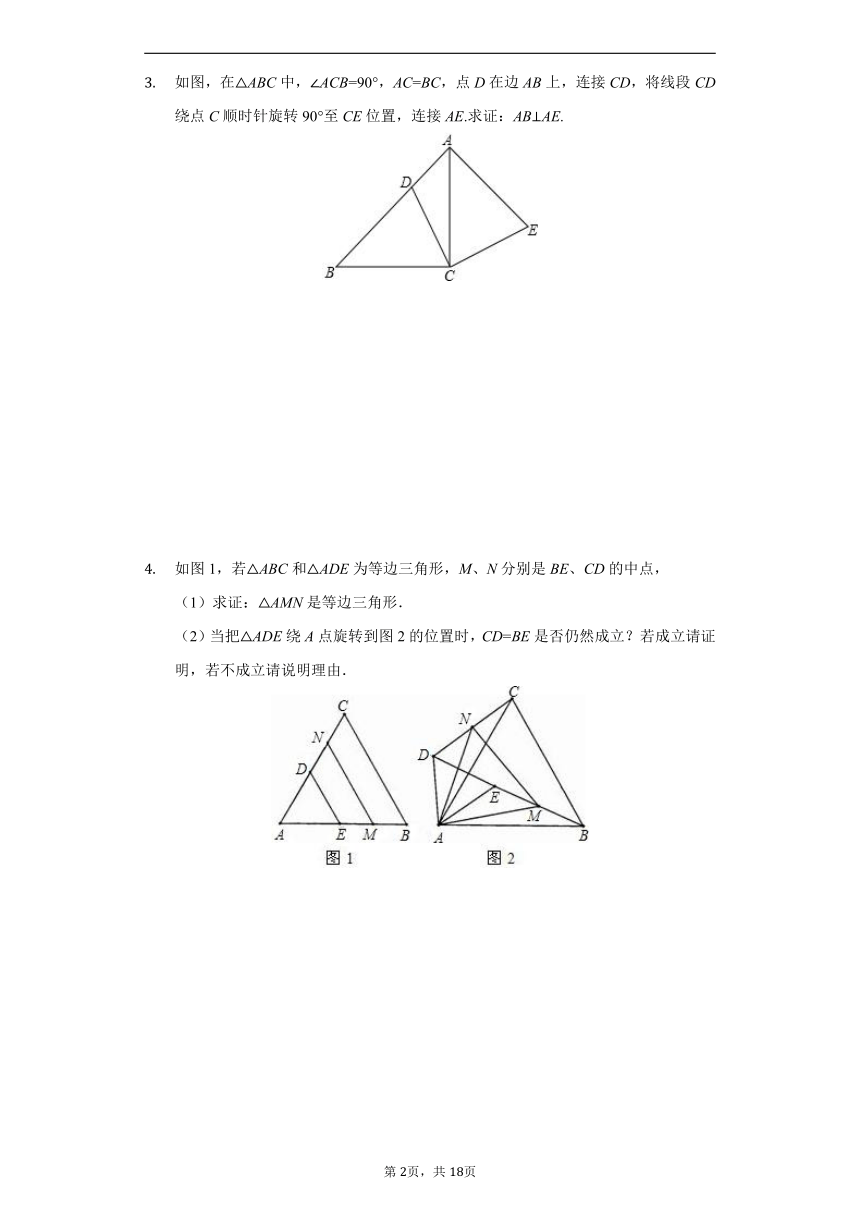
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AB⊥AE.
如图1,若△ABC和△ADE为等边三角形,M、N分别是BE、CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.
如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.当点A在线段DF的延长线上时,
(1)求证:DA=CE;
(2)判断∠DEC和∠EDC的数量关系,并说明理由;
如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°得到BE,点F是ED与AB的交点.
(1)求证:AE=CD;
(2)若∠DBC=45°,求∠BFE的度数.
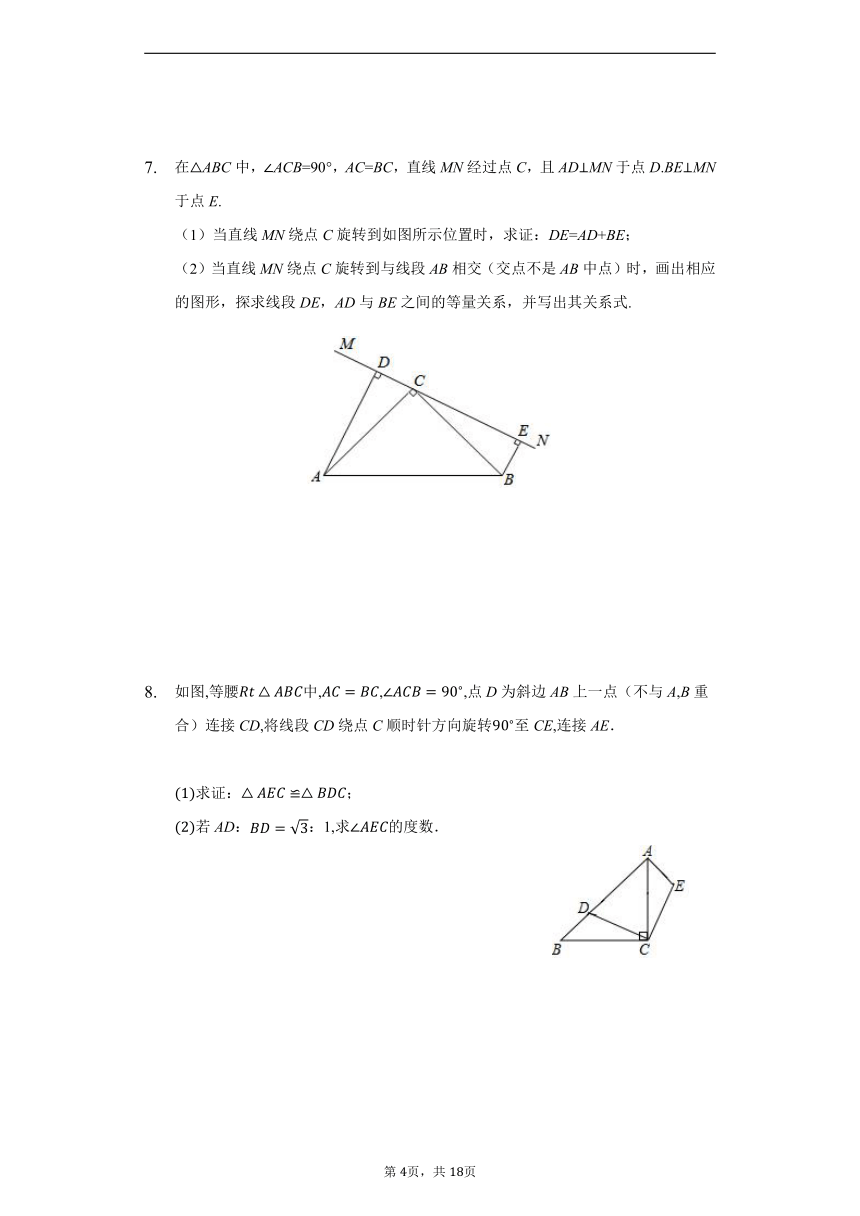
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D.BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图所示位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到与线段AB相交(交点不是AB中点)时,画出相应的图形,探求线段DE,AD与BE之间的等量关系,并写出其关系式.
如图,等腰中,,,点D为斜边AB上一点(不与A,B重合)连接CD,将线段CD绕点C顺时针方向旋转至CE,连接AE.
求证:;
若AD::1,求的度数.
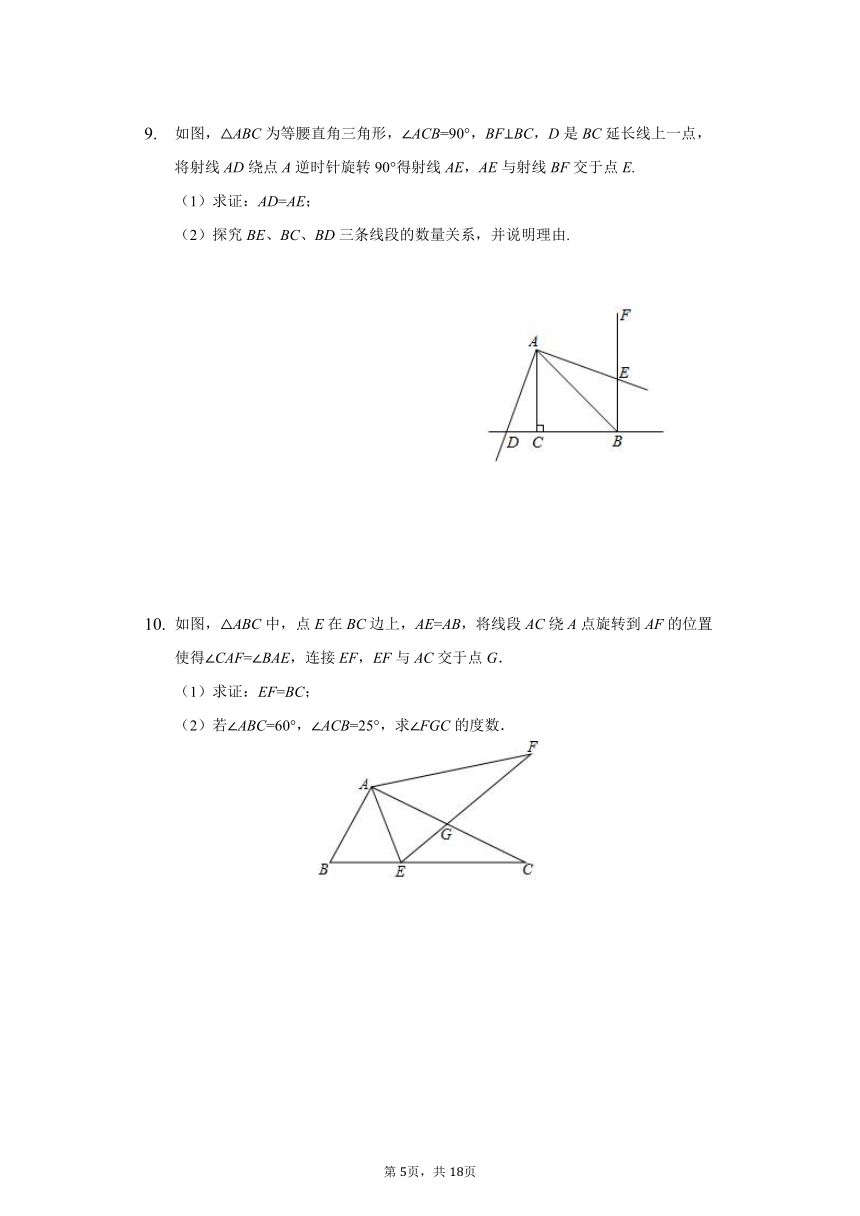
如图,△ABC为等腰直角三角形,∠ACB=90°,BF⊥BC,D是BC延长线上一点,将射线AD绕点A逆时针旋转90°得射线AE,AE与射线BF交于点E.
(1)求证:AD=AE;
(2)探究BE、BC、BD三条线段的数量关系,并说明理由.
如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=60°,∠ACB=25°,求∠FGC的度数.
几何证明题 如图,△ADE是等边三角形,点C是AD边上一点,连接DC,并将DC绕点D逆时针旋转60°,得到DB,连接AB,CB.
(1)求证:△ABD≌△ECD
(2)求∠BAE的度数;
(3)若AE=6,AC=2,求BC的长.
在△ABC中,∠ACB=90°,AC=BC,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PF,在直线AC上取点E,使CE=CP,且点F,E在直线BC的同侧,连接BE,EF.
(1)如图1,当点P在线段BC上时,求证:四边形PBEF是平行四边形;
(2)如图2,当点P在BC的延长线上时,四边形PBEF是否还是平行四边形,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按逆时针方向旋转90°后得到CE,连接EF.求证:BD=FE.
四边形ABCD中,∠DAB=60°,AB=AD,线段BC绕点B顺时针旋转60°得到线段BE,连接AC、ED、BD,求证:AC=DE.
如图,在△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A顺时针旋转45°后得到△ADE,再将△ADE绕点A顺时针旋转45°后得到△AFG,连接BE,DG,交于点M.
(1)求证:△ABE≌△ADG;
(2)求∠DME的度数.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.
参考答案
1.解: ABO与CDO关于点O成中心对称,
BO=DO,AO=CO.
AF=CE,AO-AF=CO-CE,FO=EO.
在FOD和EOB中,
FODEOB,
FD=BE.
2.证明:(1)∵∠EAC=∠DAB,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∵,
∴△ABC≌△ADE(ASA);
(2)∵△ABC≌△ADE,
∴AC=AE,
∴∠C=∠AEC=70°,
∴∠CAE=180°-∠C-∠AEC=40°,
∴∠BAD=40°.
3.证明:∵∠ACB=90°,AC=BC,
∴△ABC为等腰直角三角形,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∴△CBD绕点C顺时针旋转90°得到△CAE,
∴∠CAE=∠CBD=45°,
∴∠BAE=∠BAC+∠CAE=90°,
∴AB⊥AE.
4.证明:(1)∵△ABC和△ADE为等边三角形,
∴AB=AC、AE=AD、∠BAC=∠EAD=60°,
∴AB-AE=AC-AD,即BE=CD,
∵M、N分别是BE、CD的中点,
∴EM=BE、DN=DC,
∴EM+AE=DN+AD,即AM=AN,
∵∠BAC=60°,
∴△AMN为等边三角形;
(2)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∵∠BAE=∠BAC-∠EAC=60°-∠EAC,
∠DAC=∠DAE-∠EAC=60°-∠EAC,
∴∠BAE=∠DAC,
在△DAC和△EAB中,
∵,
∴△DAC≌△EAB(SAS),
∴CD=BE.
5.(1)证明:∵把BA顺时针方向旋转60°至BE,
∴BA=BE,∠ABE=60°,
在等边△BCD中,DB=BC,∠DBC=60°,
∴∠DBA=∠DBC+∠FBA=60°+∠FBA,
∵∠CBE=60°+∠FBA,
∴∠DBA=∠CBE,
∴△BAD≌△BEC,
∴DA=CE;
(2)∠DEC+∠EDC=90°,
∵DB=DC,DA⊥BC,
∴,
∵△BAD≌△BEC,
∴∠BCE=∠BDA=30°,
在等边△BCD中,∠BCD=60°,
∴∠DCE=∠BCE+∠BCD=90°,
∴∠DEC+∠EDC=90°.
6.解:(1)证明:∵线段BD绕着点B按逆时针方向旋转120°能与BE重合,
∴BD=BE,∠EBD=120°.
∵AB=BC,∠ABC=120°,
∴∠ABD+∠DBC=∠ABD+∠EBA=120°,
∴∠DBC=∠EBA.
在△ABE和△CBD中
AB=CB,∠EBA=∠DBC,BE=BD,
∴△ABE≌△CBD(SAS),
∴AE=CD.
(2)解:由(1)知∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,
∴∠BED=∠BDE=(180°-120°)=30°,
∴∠BFE=180°﹣∠BED﹣∠ABE=180°-30°-45°=105°.
7.(1)证明:如图1,
∵AD⊥MN于点D.BE⊥MN于点E,
∴∠ADC=90°,∠CEB=90°,
∵∠ACB=90°,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE;
(2)如图2,DE=AD-BE;
如图3,DE=BE-AD.
8.解:(1)∵将线段CD绕点C顺时针方向旋转90°至CE,
∴∠ACB=∠DCE=90°,DC=EC,
∴∠BCD=∠ACE
而BC=AC,
∴△ACE≌△BCD(SAS);
(2)连接DE,
∵∠DCE=90°,DC=CE,
∴∠DEC=45°,
由(1)知△ACE≌△BCD,
∴BD=AE,∠B=∠CAE=45°,
∴∠BAE=∠BAC+∠CAE=45°+45°=90°,
∵AD:BD=:1,
∴AD:AE=,
∴AE:DE=,即AE=DE,
∴在Rt△DAE中,,
∴∠AED=60°,
∴∠AEC=∠AED+∠DEC=60°+45°=105°.
9.(1)证明:过A点作AM⊥BF于M,如图,
∵BF⊥BC,
∴∠CBM=90°,
∵△ABC为等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴四边形ACBM为正方形,
∴AC=AM,∠CAM=90°,
∵射线AD绕点A逆时针旋转90°得射线AE,
∴∠DAE=90°,
∵∠DAC+∠CAE=90°,∠EAM+∠CAE=90°,
∴∠DAC=∠EAM,
在△ACD和△AME中,
,
∴△ACD≌△AME(ASA),
∴AD=AE;
(2)BD+BE=2BC.
理由如下:∵△ACD≌△AME,
∴CD=ME,
∵四边形ACBM为正方形,
∴BM=BC,
∴BD+BE=BC+CD+BM-ME=BC+ME+BC-ME=2BC.
10.(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF.
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF.
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)解:∵AB=AE,∠ABC=60°,
∴∠BAE=180°-60°×2=60°,
∴∠FAG=∠BAE=60°.
∵△ABC≌△AEF,
∴∠F=∠C=25°,
∴∠FGC=∠FAG+∠F=60°+25°=85°.
11.(1)证明:∵△ADE是等边三角形
∴AD=DE ∠ADE=60°
由旋转可知DB=DC ∠BDC=60°
∴∠ADB=∠CDE
在△ABD和△ECD中
∴△ABD≌△ECD(SAS)
(2)∵△ABD≌△ECD
∴∠BAD=∠CED
∵△ADE是等边三角形
∴∠CED=∠EAD=60°
∴∠BAD=60°
∴∠BAE=∠BAD+∠EAD=60°+60°=120°
答:∠BAE的度数为120°
(3)过点D作DF⊥AE于点F,
∵△ADE是等边三角形,
∴,AD=AE=6,∠ADE=60°,
∴,CF=AF-AC=1,
∴,
∵△ABD≌△ECD
∴∠ADB=∠CDE,BD=CD,
∴∠BDC=∠ADE=60°,
∴△BCD为等边三角形,
∴.
12.证明:(1)∵AB=BC,∠ACB=90°,
∴∠ACB=∠ACP=90°.
∵CE=CP,
∴△ACP≌△BCE.
∴AP=BE,∠APC=∠BEC.
∵线段PA绕点P逆时针旋转90度得到线段PF,
∴PA=PF,∠APF=90°.
∴BE=PF,∠APC+∠CPF=90°.
∵∠CBE+∠BEC=90°,
∴∠CBE=∠CPF.
∴BE∥PF.
∴四边形PBEF是平行四边形.
(2)∵AC=BC,∠ACB=90°,
∴∠ACB=∠ACP=90°.
∵CE=CP,
∴△ACP≌△BCE.
∴AP=BE,∠PAC=∠EBC.
∵线段PA绕点P逆时针旋转90度得到线段PF,
∴PA=PF,∠APF=90°.
∴BE=PF.
∵∠PAC+∠APC=90°,
∴∠EBC+∠APC=90°.
∵∠APF=90°,
∴∠APF+∠EBC+∠APC=180°,
即∠FPB+∠PBE=180°.
∴BE∥PF.
∴四边形PBEF是平行四边形.
13.证明:∵将线段CD绕点C按逆时针方向旋转90°后得到线段CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=∠FCE=90°-∠ACD,
在△BCD和△FCE中,
∴△BCD≌△FCE(SAS),
∴BD=FE;
14.证明:∵∠DAB=60 ,AB=AD,
∴△ABD是等边三角形,
∴AB=DB,∠ABD=60 ,
∵线段BC绕点B顺时针旋转60 得到线段B,
∴CB=EB,∠CBE=60 ,
∴∠ABC=∠DBE,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(SAS),
∴AC=DE.
15.解:(1)证明:由旋转的定义可得,
△ABC≌△ADE,△ADE≌△AFG,
∴AB=AD,AE=AG,∠BAD=∠DAE=∠FAG=45°,
∴∠BAE=∠DAG=90°,
∴在△ABE与△ADG中,
∴△ABE≌△ADG(SAS).
(2)记BE与AD的交点为N,
∵△ABE≌△ADG,
∴∠MDA=∠MBA,
∵∠DME=∠MDA+∠DNM,
∴∠DME=∠MBA+∠ANB,
在△ABN中,∵∠BAD=45°,
∴∠MBA+∠ANB=135°,
∴∠DME=135°.
16.证明:(1)由旋转的性质得,CD=CF,∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠BCD+∠DCE=90°,
∴∠BCD=∠ECF,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS);
(2)∵EF∥CD,
∴∠F+∠DCF=180°,
∵∠DCF=90°,
∴∠F=90°,
∵△BDC≌△EFC,
∴∠BDC=∠F=90°.
第8页,共18页
第9页,共18页
第二十三章旋转——证明题基础篇1
如图,ABO与CDO关于点O成中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.
在△ABC和△ADE中,点E在BC边上,∠EAC=∠DAB,∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)将△ABC绕着点A旋转得到△ADE,如果∠AEC=70°,求∠BAD的度数.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AB⊥AE.
如图1,若△ABC和△ADE为等边三角形,M、N分别是BE、CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.
如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.当点A在线段DF的延长线上时,
(1)求证:DA=CE;
(2)判断∠DEC和∠EDC的数量关系,并说明理由;
如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°得到BE,点F是ED与AB的交点.
(1)求证:AE=CD;
(2)若∠DBC=45°,求∠BFE的度数.
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D.BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图所示位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到与线段AB相交(交点不是AB中点)时,画出相应的图形,探求线段DE,AD与BE之间的等量关系,并写出其关系式.
如图,等腰中,,,点D为斜边AB上一点(不与A,B重合)连接CD,将线段CD绕点C顺时针方向旋转至CE,连接AE.
求证:;
若AD::1,求的度数.
如图,△ABC为等腰直角三角形,∠ACB=90°,BF⊥BC,D是BC延长线上一点,将射线AD绕点A逆时针旋转90°得射线AE,AE与射线BF交于点E.
(1)求证:AD=AE;
(2)探究BE、BC、BD三条线段的数量关系,并说明理由.
如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=60°,∠ACB=25°,求∠FGC的度数.
几何证明题 如图,△ADE是等边三角形,点C是AD边上一点,连接DC,并将DC绕点D逆时针旋转60°,得到DB,连接AB,CB.
(1)求证:△ABD≌△ECD
(2)求∠BAE的度数;
(3)若AE=6,AC=2,求BC的长.
在△ABC中,∠ACB=90°,AC=BC,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PF,在直线AC上取点E,使CE=CP,且点F,E在直线BC的同侧,连接BE,EF.
(1)如图1,当点P在线段BC上时,求证:四边形PBEF是平行四边形;
(2)如图2,当点P在BC的延长线上时,四边形PBEF是否还是平行四边形,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按逆时针方向旋转90°后得到CE,连接EF.求证:BD=FE.
四边形ABCD中,∠DAB=60°,AB=AD,线段BC绕点B顺时针旋转60°得到线段BE,连接AC、ED、BD,求证:AC=DE.
如图,在△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A顺时针旋转45°后得到△ADE,再将△ADE绕点A顺时针旋转45°后得到△AFG,连接BE,DG,交于点M.
(1)求证:△ABE≌△ADG;
(2)求∠DME的度数.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.
参考答案
1.解: ABO与CDO关于点O成中心对称,
BO=DO,AO=CO.
AF=CE,AO-AF=CO-CE,FO=EO.
在FOD和EOB中,
FODEOB,
FD=BE.
2.证明:(1)∵∠EAC=∠DAB,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∵,
∴△ABC≌△ADE(ASA);
(2)∵△ABC≌△ADE,
∴AC=AE,
∴∠C=∠AEC=70°,
∴∠CAE=180°-∠C-∠AEC=40°,
∴∠BAD=40°.
3.证明:∵∠ACB=90°,AC=BC,
∴△ABC为等腰直角三角形,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∴△CBD绕点C顺时针旋转90°得到△CAE,
∴∠CAE=∠CBD=45°,
∴∠BAE=∠BAC+∠CAE=90°,
∴AB⊥AE.
4.证明:(1)∵△ABC和△ADE为等边三角形,
∴AB=AC、AE=AD、∠BAC=∠EAD=60°,
∴AB-AE=AC-AD,即BE=CD,
∵M、N分别是BE、CD的中点,
∴EM=BE、DN=DC,
∴EM+AE=DN+AD,即AM=AN,
∵∠BAC=60°,
∴△AMN为等边三角形;
(2)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∵∠BAE=∠BAC-∠EAC=60°-∠EAC,
∠DAC=∠DAE-∠EAC=60°-∠EAC,
∴∠BAE=∠DAC,
在△DAC和△EAB中,
∵,
∴△DAC≌△EAB(SAS),
∴CD=BE.
5.(1)证明:∵把BA顺时针方向旋转60°至BE,
∴BA=BE,∠ABE=60°,
在等边△BCD中,DB=BC,∠DBC=60°,
∴∠DBA=∠DBC+∠FBA=60°+∠FBA,
∵∠CBE=60°+∠FBA,
∴∠DBA=∠CBE,
∴△BAD≌△BEC,
∴DA=CE;
(2)∠DEC+∠EDC=90°,
∵DB=DC,DA⊥BC,
∴,
∵△BAD≌△BEC,
∴∠BCE=∠BDA=30°,
在等边△BCD中,∠BCD=60°,
∴∠DCE=∠BCE+∠BCD=90°,
∴∠DEC+∠EDC=90°.
6.解:(1)证明:∵线段BD绕着点B按逆时针方向旋转120°能与BE重合,
∴BD=BE,∠EBD=120°.
∵AB=BC,∠ABC=120°,
∴∠ABD+∠DBC=∠ABD+∠EBA=120°,
∴∠DBC=∠EBA.
在△ABE和△CBD中
AB=CB,∠EBA=∠DBC,BE=BD,
∴△ABE≌△CBD(SAS),
∴AE=CD.
(2)解:由(1)知∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,
∴∠BED=∠BDE=(180°-120°)=30°,
∴∠BFE=180°﹣∠BED﹣∠ABE=180°-30°-45°=105°.
7.(1)证明:如图1,
∵AD⊥MN于点D.BE⊥MN于点E,
∴∠ADC=90°,∠CEB=90°,
∵∠ACB=90°,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE;
(2)如图2,DE=AD-BE;
如图3,DE=BE-AD.
8.解:(1)∵将线段CD绕点C顺时针方向旋转90°至CE,
∴∠ACB=∠DCE=90°,DC=EC,
∴∠BCD=∠ACE
而BC=AC,
∴△ACE≌△BCD(SAS);
(2)连接DE,
∵∠DCE=90°,DC=CE,
∴∠DEC=45°,
由(1)知△ACE≌△BCD,
∴BD=AE,∠B=∠CAE=45°,
∴∠BAE=∠BAC+∠CAE=45°+45°=90°,
∵AD:BD=:1,
∴AD:AE=,
∴AE:DE=,即AE=DE,
∴在Rt△DAE中,,
∴∠AED=60°,
∴∠AEC=∠AED+∠DEC=60°+45°=105°.
9.(1)证明:过A点作AM⊥BF于M,如图,
∵BF⊥BC,
∴∠CBM=90°,
∵△ABC为等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴四边形ACBM为正方形,
∴AC=AM,∠CAM=90°,
∵射线AD绕点A逆时针旋转90°得射线AE,
∴∠DAE=90°,
∵∠DAC+∠CAE=90°,∠EAM+∠CAE=90°,
∴∠DAC=∠EAM,
在△ACD和△AME中,
,
∴△ACD≌△AME(ASA),
∴AD=AE;
(2)BD+BE=2BC.
理由如下:∵△ACD≌△AME,
∴CD=ME,
∵四边形ACBM为正方形,
∴BM=BC,
∴BD+BE=BC+CD+BM-ME=BC+ME+BC-ME=2BC.
10.(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF.
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF.
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)解:∵AB=AE,∠ABC=60°,
∴∠BAE=180°-60°×2=60°,
∴∠FAG=∠BAE=60°.
∵△ABC≌△AEF,
∴∠F=∠C=25°,
∴∠FGC=∠FAG+∠F=60°+25°=85°.
11.(1)证明:∵△ADE是等边三角形
∴AD=DE ∠ADE=60°
由旋转可知DB=DC ∠BDC=60°
∴∠ADB=∠CDE
在△ABD和△ECD中
∴△ABD≌△ECD(SAS)
(2)∵△ABD≌△ECD
∴∠BAD=∠CED
∵△ADE是等边三角形
∴∠CED=∠EAD=60°
∴∠BAD=60°
∴∠BAE=∠BAD+∠EAD=60°+60°=120°
答:∠BAE的度数为120°
(3)过点D作DF⊥AE于点F,
∵△ADE是等边三角形,
∴,AD=AE=6,∠ADE=60°,
∴,CF=AF-AC=1,
∴,
∵△ABD≌△ECD
∴∠ADB=∠CDE,BD=CD,
∴∠BDC=∠ADE=60°,
∴△BCD为等边三角形,
∴.
12.证明:(1)∵AB=BC,∠ACB=90°,
∴∠ACB=∠ACP=90°.
∵CE=CP,
∴△ACP≌△BCE.
∴AP=BE,∠APC=∠BEC.
∵线段PA绕点P逆时针旋转90度得到线段PF,
∴PA=PF,∠APF=90°.
∴BE=PF,∠APC+∠CPF=90°.
∵∠CBE+∠BEC=90°,
∴∠CBE=∠CPF.
∴BE∥PF.
∴四边形PBEF是平行四边形.
(2)∵AC=BC,∠ACB=90°,
∴∠ACB=∠ACP=90°.
∵CE=CP,
∴△ACP≌△BCE.
∴AP=BE,∠PAC=∠EBC.
∵线段PA绕点P逆时针旋转90度得到线段PF,
∴PA=PF,∠APF=90°.
∴BE=PF.
∵∠PAC+∠APC=90°,
∴∠EBC+∠APC=90°.
∵∠APF=90°,
∴∠APF+∠EBC+∠APC=180°,
即∠FPB+∠PBE=180°.
∴BE∥PF.
∴四边形PBEF是平行四边形.
13.证明:∵将线段CD绕点C按逆时针方向旋转90°后得到线段CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=∠FCE=90°-∠ACD,
在△BCD和△FCE中,
∴△BCD≌△FCE(SAS),
∴BD=FE;
14.证明:∵∠DAB=60 ,AB=AD,
∴△ABD是等边三角形,
∴AB=DB,∠ABD=60 ,
∵线段BC绕点B顺时针旋转60 得到线段B,
∴CB=EB,∠CBE=60 ,
∴∠ABC=∠DBE,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(SAS),
∴AC=DE.
15.解:(1)证明:由旋转的定义可得,
△ABC≌△ADE,△ADE≌△AFG,
∴AB=AD,AE=AG,∠BAD=∠DAE=∠FAG=45°,
∴∠BAE=∠DAG=90°,
∴在△ABE与△ADG中,
∴△ABE≌△ADG(SAS).
(2)记BE与AD的交点为N,
∵△ABE≌△ADG,
∴∠MDA=∠MBA,
∵∠DME=∠MDA+∠DNM,
∴∠DME=∠MBA+∠ANB,
在△ABN中,∵∠BAD=45°,
∴∠MBA+∠ANB=135°,
∴∠DME=135°.
16.证明:(1)由旋转的性质得,CD=CF,∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠BCD+∠DCE=90°,
∴∠BCD=∠ECF,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS);
(2)∵EF∥CD,
∴∠F+∠DCF=180°,
∵∠DCF=90°,
∴∠F=90°,
∵△BDC≌△EFC,
∴∠BDC=∠F=90°.
第8页,共18页
第9页,共18页
同课章节目录
