2021-2022学年人教版数学八年级上册 _14.1.4 整式乘法第二课时(单项式乘多项式) 课件(15张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 _14.1.4 整式乘法第二课时(单项式乘多项式) 课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 13:10:20 | ||
图片预览





文档简介
(共15张PPT)
整 式 的 乘 法 第 二 课 时
单 项 式 X 多 项 式
回顾旧知
1、同底数幂的乘法:
am·an=am+n(m,n都是正整数)
即同底数幂相乘,底数不变,指数相加.
快问快答
(1) (2) (3)
(ab)n=anbn(n为正整数)
即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(am)n=amn(m,n都是正整数)
即幂的乘方,底数不变,指数相乘.
2、幂的乘方
(1)、(b3)3
(2)、x4·x4
(3)、 (x4)7
3、积的乘方
(1)、(2a)3 (2)、(-5b)3 (3)、(xy2)2
4、单项式 X 单项式的法则
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)、
(2)、
(3)、
(4)、
问题引入
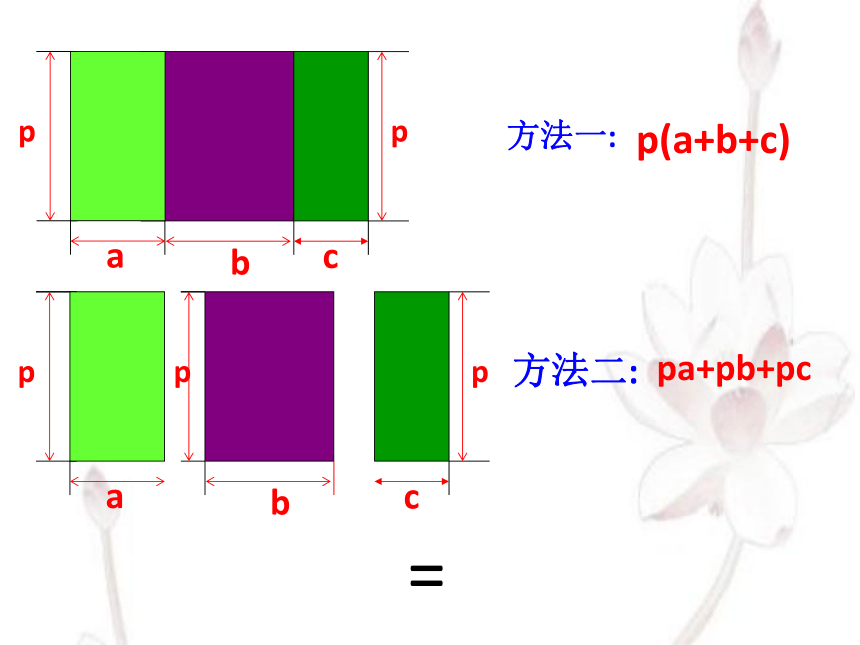
为了扩大绿地面积,台州市有计划要把临海—仙居的一段公路中的长a米,宽p米的长方形花草隔离带向两边分别加宽a米和c米,你能用几种方法表示扩大后的花草隔离带面积 不同的表示方法之间有什么关系
根据题意画出的设计图应该是怎样的呢?
m
b
p
a
p
c
p
b
p
c
p
a
方法二:
方法一:
=
p(a+b+c)
pa+pb+pc
思路:
单×多
转 化
分配律
单×单
p(a+b+c)
=
pa+pb+pc
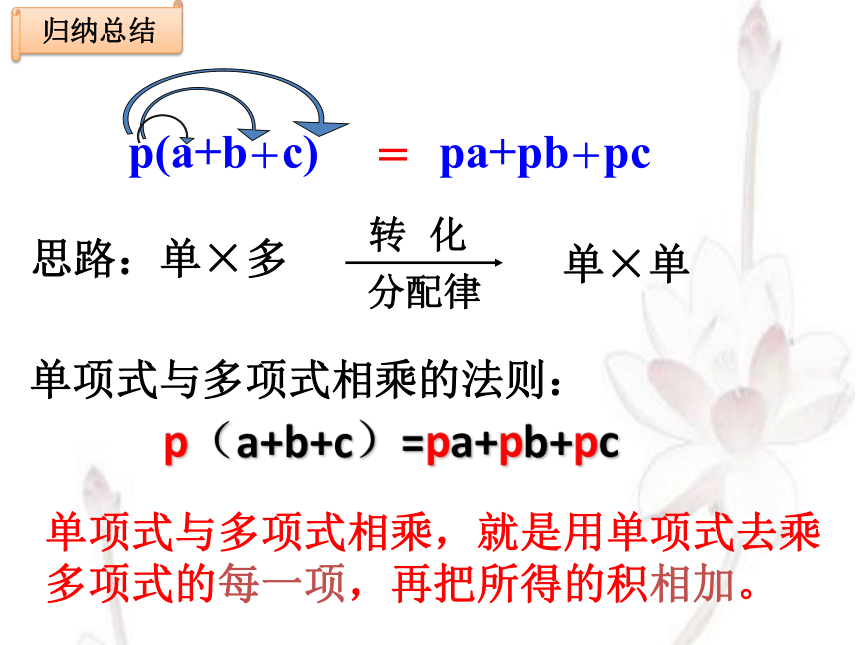
归纳总结
单项式与多项式相乘的法则:
p(a+b+c)=pa+pb+pc
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。
例题讲解
单项式X多项式的法则是什么呢?
例题 :单项式 X 多项式
(1)
解:原式=
(2)
解:原式=
(3)
解:原式=
1、有乘方先算乘方
2、要将括号外的单项式与括号内的每一项都相乘
3、注意符号
习题巩固
1、判断
×
(1)m(a+b+c+d)=ma+b+c+d( )
(2)(-2x) (ax+b-3)=-2ax2-2bx-6x( )
×
如果错误的话,请说明错误的理由,并加以改正。
2、选择
C
下列计算正确的是( )
A、
B、
C、
D、
3、请下列各式的值
-2x(3x2-5x+1)
(2) (2ab2-3ab)3ab
(3) (x2-2p)·(xy2)2
请上台来,开始你的表演!
4、某同学在计算一个多项式乘以
解:设这个
∴
∴
今天我们主要学习了什么呢?
课堂小结
探索并了解单项式与多项式相乘的法则,并运用它们进行计算。
1、计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负。
不要出现漏乘现象。
运算要有顺序:先乘方,再乘除,最后加减。
对于混合运算,注意最后应合并同类项。
单项式 X 单项式的法则
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
p(a+b+c)=pa+pb+pc
整 式 的 乘 法 第 二 课 时
单 项 式 X 多 项 式
回顾旧知
1、同底数幂的乘法:
am·an=am+n(m,n都是正整数)
即同底数幂相乘,底数不变,指数相加.
快问快答
(1) (2) (3)
(ab)n=anbn(n为正整数)
即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(am)n=amn(m,n都是正整数)
即幂的乘方,底数不变,指数相乘.
2、幂的乘方
(1)、(b3)3
(2)、x4·x4
(3)、 (x4)7
3、积的乘方
(1)、(2a)3 (2)、(-5b)3 (3)、(xy2)2
4、单项式 X 单项式的法则
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)、
(2)、
(3)、
(4)、
问题引入
为了扩大绿地面积,台州市有计划要把临海—仙居的一段公路中的长a米,宽p米的长方形花草隔离带向两边分别加宽a米和c米,你能用几种方法表示扩大后的花草隔离带面积 不同的表示方法之间有什么关系
根据题意画出的设计图应该是怎样的呢?
m
b
p
a
p
c
p
b
p
c
p
a
方法二:
方法一:
=
p(a+b+c)
pa+pb+pc
思路:
单×多
转 化
分配律
单×单
p(a+b+c)
=
pa+pb+pc
归纳总结
单项式与多项式相乘的法则:
p(a+b+c)=pa+pb+pc
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。
例题讲解
单项式X多项式的法则是什么呢?
例题 :单项式 X 多项式
(1)
解:原式=
(2)
解:原式=
(3)
解:原式=
1、有乘方先算乘方
2、要将括号外的单项式与括号内的每一项都相乘
3、注意符号
习题巩固
1、判断
×
(1)m(a+b+c+d)=ma+b+c+d( )
(2)(-2x) (ax+b-3)=-2ax2-2bx-6x( )
×
如果错误的话,请说明错误的理由,并加以改正。
2、选择
C
下列计算正确的是( )
A、
B、
C、
D、
3、请下列各式的值
-2x(3x2-5x+1)
(2) (2ab2-3ab)3ab
(3) (x2-2p)·(xy2)2
请上台来,开始你的表演!
4、某同学在计算一个多项式乘以
解:设这个
∴
∴
今天我们主要学习了什么呢?
课堂小结
探索并了解单项式与多项式相乘的法则,并运用它们进行计算。
1、计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负。
不要出现漏乘现象。
运算要有顺序:先乘方,再乘除,最后加减。
对于混合运算,注意最后应合并同类项。
单项式 X 单项式的法则
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
p(a+b+c)=pa+pb+pc
