13.3.2 第1课时 等边三角形的性质和判定 课件(共24张PPT)
文档属性
| 名称 | 13.3.2 第1课时 等边三角形的性质和判定 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第十三章 轴对称
13.3.2 第1课时
等边三角形的性质与判定
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
知识回顾
等腰三角形
等边三角形
一般三角形
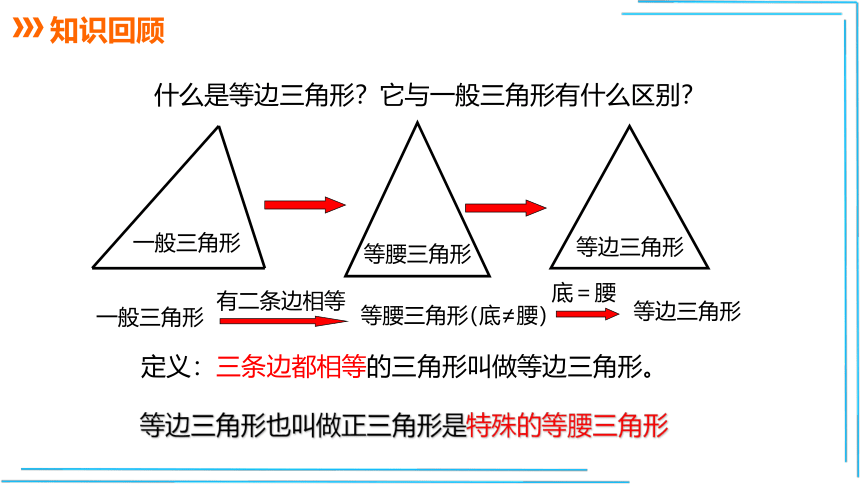
定义:三条边都相等的三角形叫做等边三角形。
一般三角形
等腰三角形
等边三角形
(底≠腰)
底=腰
有二条边相等
什么是等边三角形?它与一般三角形有什么区别?
等边三角形也叫做正三角形是特殊的等腰三角形
名称 图 形 定 义 性 质 判 定
等 腰 三 角 形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
获取新知
知识点一:等边三角形的性质
几何语言:
∵△ABC是等边三角形
∴AB=BC=AC
A
B
C
1.由定义可知:等边三角形三条边都相等.
A
B
C
A
B
C
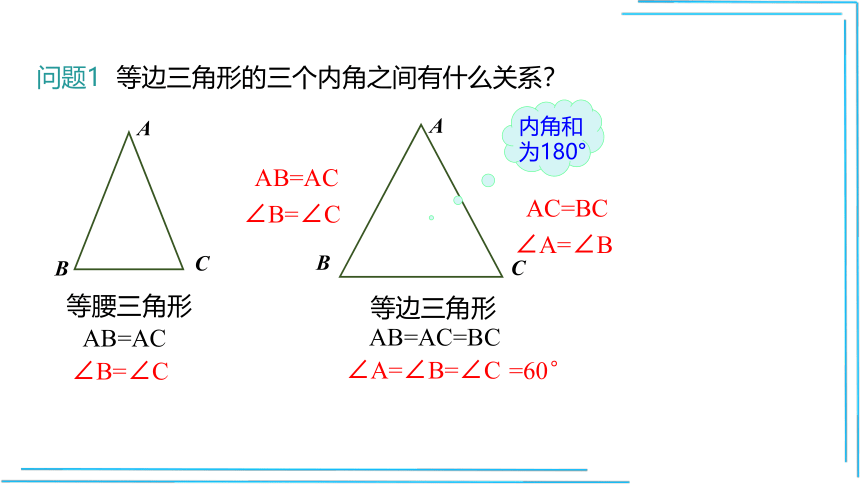
问题1 等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
内角和为180°
=60°
结论: 等边三角形的三个内角都相等,并且每一 个角都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
2. 等边三角形的三个内角都相等,并且每一个角都等于60°.
几何语言:
在△ABC中
∵AB=AC=BC
∴∠A=∠B=∠C=60°
A
B
C
A
B
C
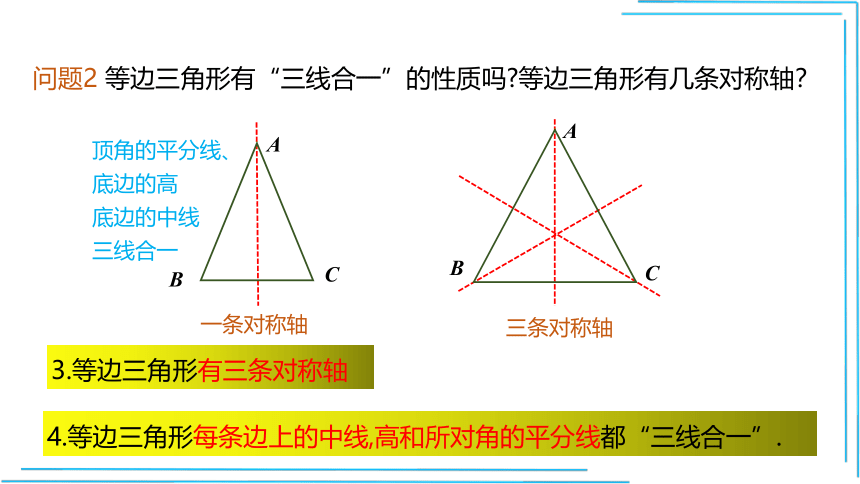
问题2 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
4.等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
3.等边三角形有三条对称轴
知识要点
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
A
B
C
D
E
F
利用等边三角形三线合一填空:
∵ AB=AC,BD=DC
∴∠ =∠ , ⊥ ;
∵ AB=BC,AE=EC
∴∠ =∠ , ⊥ ;
∵ AC=BC,AF=FB
∴∠ =∠ , ⊥ .
BAD
CAD
AD
BC
ABE
CBE
BE
AC
ACF
BCF
CF
AB
练习
例题讲解
例1 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
知识点二:等边三角形的判定
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
还有其他的判定方法吗?
知识要点
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
A
B
C
几何语言:
在△ABC中
∵AB=AC,∠A=60°
∴AB=BC=AC
已知:AB=AC,∠B=60°.
求证:AB=BC=BC.
证明:∵AB=AC
∴∠B=∠C=60°
∵∠A=180°-∠B-∠C
∴∠A=180°-60°-60°=60°
∴∠A=∠B=∠C
∴AB=BC=AC
A
B
C
验证结论
例题讲解
例2 如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.
变式1 若点D、E 在边AB、AC 的延长线上,且 DE∥BC,结论还成立吗?
A
D
E
B
C
变式2 若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
随堂演练
D
1.下列关于“等边三角形”的说法不正确的是( )
A.等边三角形的三条边都相等
B.等边三角形的三个内角都相等且都等于60°
C.等边三角形是轴对称图形,有三条对称轴
D.等边三角形与等腰三角形具有相同的性质
2.给出下列几种三角形:①三个角都相等的三角形;②有两个角等于60°的三角形;③有一个角是60°的等腰三角形;④有两个角相等的等腰三角形.其中一定是等边三角形的有( )
A.0种 B.1种 C.2种 D.3种
D
3.在等边三角形ABC中,AD⊥BC于点D,则∠BAD=________°.
4.在等腰三角形ABC中,AB=AC,∠B=60°,则∠A=________°.
30
60
5.如图,A、O、D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A、O、D三点共线,
∴ ∠DOB=∠COA=120°,
∴ △COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
课堂小结
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
https://www.21cnjy.com/help/help_extract.php
第十三章 轴对称
13.3.2 第1课时
等边三角形的性质与判定
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
知识回顾
等腰三角形
等边三角形
一般三角形
定义:三条边都相等的三角形叫做等边三角形。
一般三角形
等腰三角形
等边三角形
(底≠腰)
底=腰
有二条边相等
什么是等边三角形?它与一般三角形有什么区别?
等边三角形也叫做正三角形是特殊的等腰三角形
名称 图 形 定 义 性 质 判 定
等 腰 三 角 形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
获取新知
知识点一:等边三角形的性质
几何语言:
∵△ABC是等边三角形
∴AB=BC=AC
A
B
C
1.由定义可知:等边三角形三条边都相等.
A
B
C
A
B
C
问题1 等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
内角和为180°
=60°
结论: 等边三角形的三个内角都相等,并且每一 个角都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
2. 等边三角形的三个内角都相等,并且每一个角都等于60°.
几何语言:
在△ABC中
∵AB=AC=BC
∴∠A=∠B=∠C=60°
A
B
C
A
B
C
问题2 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
4.等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
3.等边三角形有三条对称轴
知识要点
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
A
B
C
D
E
F
利用等边三角形三线合一填空:
∵ AB=AC,BD=DC
∴∠ =∠ , ⊥ ;
∵ AB=BC,AE=EC
∴∠ =∠ , ⊥ ;
∵ AC=BC,AF=FB
∴∠ =∠ , ⊥ .
BAD
CAD
AD
BC
ABE
CBE
BE
AC
ACF
BCF
CF
AB
练习
例题讲解
例1 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
知识点二:等边三角形的判定
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
还有其他的判定方法吗?
知识要点
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
A
B
C
几何语言:
在△ABC中
∵AB=AC,∠A=60°
∴AB=BC=AC
已知:AB=AC,∠B=60°.
求证:AB=BC=BC.
证明:∵AB=AC
∴∠B=∠C=60°
∵∠A=180°-∠B-∠C
∴∠A=180°-60°-60°=60°
∴∠A=∠B=∠C
∴AB=BC=AC
A
B
C
验证结论
例题讲解
例2 如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.
变式1 若点D、E 在边AB、AC 的延长线上,且 DE∥BC,结论还成立吗?
A
D
E
B
C
变式2 若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
随堂演练
D
1.下列关于“等边三角形”的说法不正确的是( )
A.等边三角形的三条边都相等
B.等边三角形的三个内角都相等且都等于60°
C.等边三角形是轴对称图形,有三条对称轴
D.等边三角形与等腰三角形具有相同的性质
2.给出下列几种三角形:①三个角都相等的三角形;②有两个角等于60°的三角形;③有一个角是60°的等腰三角形;④有两个角相等的等腰三角形.其中一定是等边三角形的有( )
A.0种 B.1种 C.2种 D.3种
D
3.在等边三角形ABC中,AD⊥BC于点D,则∠BAD=________°.
4.在等腰三角形ABC中,AB=AC,∠B=60°,则∠A=________°.
30
60
5.如图,A、O、D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A、O、D三点共线,
∴ ∠DOB=∠COA=120°,
∴ △COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
课堂小结
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
https://www.21cnjy.com/help/help_extract.php
