2021-2022学年苏科版数学八年级上册第二章轴对称图形单元测试(word版无答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级上册第二章轴对称图形单元测试(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 18:48:10 | ||
图片预览

文档简介
第二章 轴对称图形单元测试
班级: 姓名:
选择题(每题3分)
1.下列四个图案中,不是轴对称图案的是( )
A B C D
2.下列语句中,正确的有 ( )
①关于一条直线对称的两个图形一定能重合; ②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴; ④两个轴对称图形的对应点一定在对称轴的两侧.
A.1个 B.2个 C.3个 D.4个
3.已知等腰三角形的两条边长分别是6和3,则下列四个数中,可以作为第三条边的长的是 ( )
A.17 B.6 C.9 D.3
4.如图,在△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交于AC于D点,则∠DBC的度数是 ( )
A.15° B.20° C.25° D.30°
(第4题) (第5题) (第6题) (第7题)
5.如图,已知△ABC的周长是16,MB和MC分别平分∠ABC和∠ACB,过点M作BC的垂线交BC于点D.且MD=4,则△ABC的面积是( )
A.64 B. 48 C. 32 D. 42
6.如图,D是△ABC中BC边上一点,AB=AC=BD,则∠1和∠2的关系是 ( )
A.∠1=2∠2 B.∠l+∠2=90° C.180°-∠1=3∠2 D.180°+∠2=3∠1
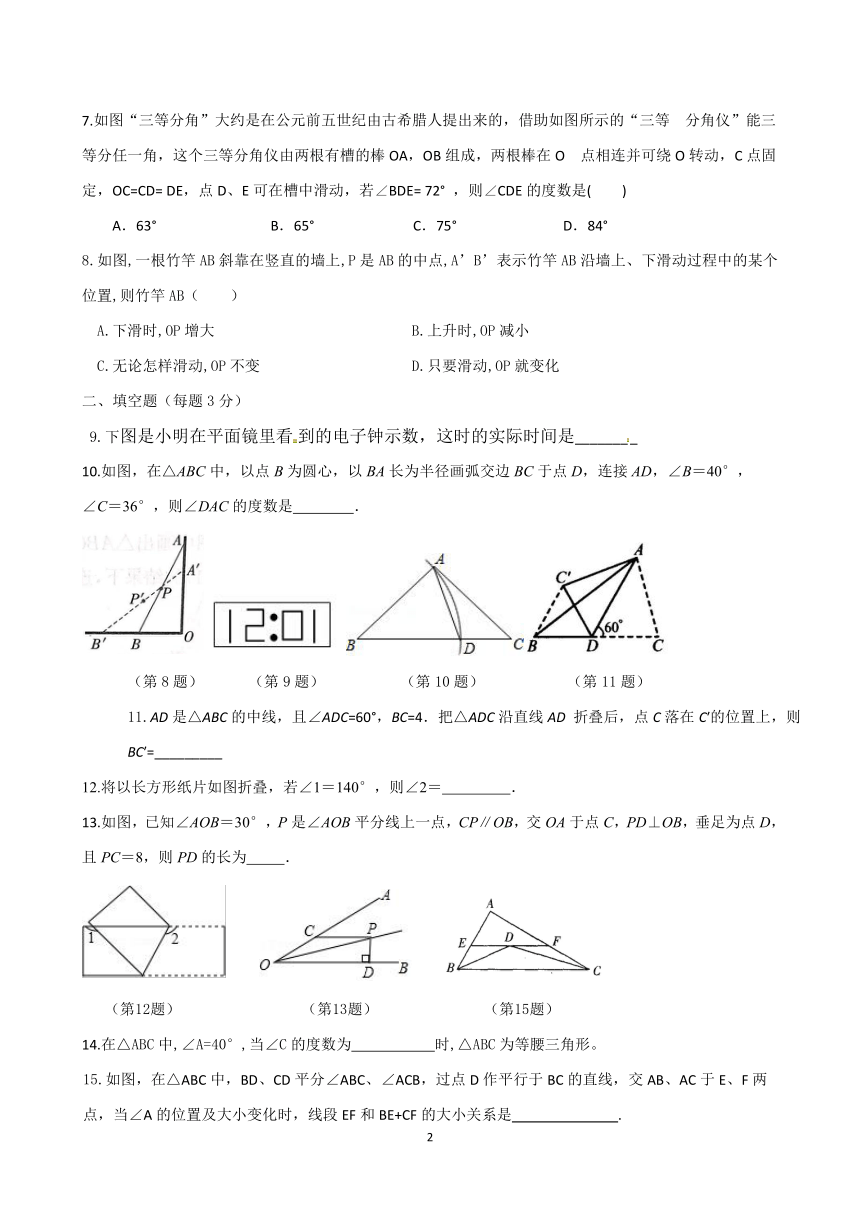
7.如图“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等 分角仪”能三
等分任一角,这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O 点相连并可绕O转动,C点固
定,OC=CD= DE,点D、E可在槽中滑动,若∠BDE= 72° ,则∠CDE的度数是( )
A.63° B.65° C.75° D.84°
8.如图,一根竹竿AB斜靠在竖直的墙上,P是AB的中点,A’B’表示竹竿AB沿墙上、下滑动过程中的某个位置,则竹竿AB( )
A.下滑时,OP增大 B.上升时,OP减小
C.无论怎样滑动,OP不变 D.只要滑动,OP就变化
二、填空题(每题3分)
9.下图是小明在平面镜里看到的电子钟示数,这时的实际时间是________
10.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD,∠B=40°,
∠C=36°,则∠DAC的度数是 .
(第8题) (第9题) (第10题) (第11题)
11.AD是△ABC的中线,且∠ADC=60°,BC=4.把△ADC沿直线AD折叠后,点C落在C′的位置上,则
BC′=_________
12.将以长方形纸片如图折叠,若∠1=140°,则∠2= .
13.如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=8,则PD的长为 .
(第12题) (第13题) (第15题)
14.在△ABC中,∠A=40°,当∠C的度数为 时,△ABC为等腰三角形。
15.如图,在△ABC中,BD、CD平分∠ABC、∠ACB,过点D作平行于BC的直线,交AB、AC于E、F两
点,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系是 .
16.在等边△ABC所在平面内找出一点,使它与三角形的任意两个顶点所组成的三角形都是等腰三角形.这样的点共有 个.
三、解答题
17.(8分)如图,在△ABC中,AB=AC,BC=BD=ED=EA.求∠A的度数.
18.(8分)如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
(8分)如图,四边形ABCD中,AB∥CD,点E为CD上一点,连接BE,AE,且BE、AE分别平分
∠ABC、∠BAD.求证:CD=AD+BC.
20.(8分)(1)如图,已知四边形ABCD,请用直尺和圆规在边BC上求作一点,使∠APB=∠CPD(不写作法,保留作图痕迹)
(2)请根据(1)的作图过程,说明∠APB=∠CPD的理由.
21.(8分)如图在△ABC中,∠CAB的平分线AD与BC的垂直平分线DG交于点D,过点D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
(1)求证:BE=CF;
(2)若AB=a,AC=b,求AE和BE的长(用含a,b的式子表示).
22.(12分)如图1,△ABC是等边三角形,D是BC边上一点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,当点D是边BC的中点时,过点D作DF//AC,交AB于点F,通过构造全等三角形,能够使问题得到解决,请直接写出AD与DE的数量关系:______;
(2)如图2,当点D是线段BC上(除B、C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并说明理由;
(3)当点D在线段BC的延长线上,且满足(其它条件不变)时,请画出图形,并直接写出△ABC与△BDE的面积之比.
班级: 姓名:
选择题(每题3分)
1.下列四个图案中,不是轴对称图案的是( )
A B C D
2.下列语句中,正确的有 ( )
①关于一条直线对称的两个图形一定能重合; ②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴; ④两个轴对称图形的对应点一定在对称轴的两侧.
A.1个 B.2个 C.3个 D.4个
3.已知等腰三角形的两条边长分别是6和3,则下列四个数中,可以作为第三条边的长的是 ( )
A.17 B.6 C.9 D.3
4.如图,在△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交于AC于D点,则∠DBC的度数是 ( )
A.15° B.20° C.25° D.30°
(第4题) (第5题) (第6题) (第7题)
5.如图,已知△ABC的周长是16,MB和MC分别平分∠ABC和∠ACB,过点M作BC的垂线交BC于点D.且MD=4,则△ABC的面积是( )
A.64 B. 48 C. 32 D. 42
6.如图,D是△ABC中BC边上一点,AB=AC=BD,则∠1和∠2的关系是 ( )
A.∠1=2∠2 B.∠l+∠2=90° C.180°-∠1=3∠2 D.180°+∠2=3∠1
7.如图“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等 分角仪”能三
等分任一角,这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O 点相连并可绕O转动,C点固
定,OC=CD= DE,点D、E可在槽中滑动,若∠BDE= 72° ,则∠CDE的度数是( )
A.63° B.65° C.75° D.84°
8.如图,一根竹竿AB斜靠在竖直的墙上,P是AB的中点,A’B’表示竹竿AB沿墙上、下滑动过程中的某个位置,则竹竿AB( )
A.下滑时,OP增大 B.上升时,OP减小
C.无论怎样滑动,OP不变 D.只要滑动,OP就变化
二、填空题(每题3分)
9.下图是小明在平面镜里看到的电子钟示数,这时的实际时间是________
10.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD,∠B=40°,
∠C=36°,则∠DAC的度数是 .
(第8题) (第9题) (第10题) (第11题)
11.AD是△ABC的中线,且∠ADC=60°,BC=4.把△ADC沿直线AD折叠后,点C落在C′的位置上,则
BC′=_________
12.将以长方形纸片如图折叠,若∠1=140°,则∠2= .
13.如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=8,则PD的长为 .
(第12题) (第13题) (第15题)
14.在△ABC中,∠A=40°,当∠C的度数为 时,△ABC为等腰三角形。
15.如图,在△ABC中,BD、CD平分∠ABC、∠ACB,过点D作平行于BC的直线,交AB、AC于E、F两
点,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系是 .
16.在等边△ABC所在平面内找出一点,使它与三角形的任意两个顶点所组成的三角形都是等腰三角形.这样的点共有 个.
三、解答题
17.(8分)如图,在△ABC中,AB=AC,BC=BD=ED=EA.求∠A的度数.
18.(8分)如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
(8分)如图,四边形ABCD中,AB∥CD,点E为CD上一点,连接BE,AE,且BE、AE分别平分
∠ABC、∠BAD.求证:CD=AD+BC.
20.(8分)(1)如图,已知四边形ABCD,请用直尺和圆规在边BC上求作一点,使∠APB=∠CPD(不写作法,保留作图痕迹)
(2)请根据(1)的作图过程,说明∠APB=∠CPD的理由.
21.(8分)如图在△ABC中,∠CAB的平分线AD与BC的垂直平分线DG交于点D,过点D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
(1)求证:BE=CF;
(2)若AB=a,AC=b,求AE和BE的长(用含a,b的式子表示).
22.(12分)如图1,△ABC是等边三角形,D是BC边上一点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,当点D是边BC的中点时,过点D作DF//AC,交AB于点F,通过构造全等三角形,能够使问题得到解决,请直接写出AD与DE的数量关系:______;
(2)如图2,当点D是线段BC上(除B、C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并说明理由;
(3)当点D在线段BC的延长线上,且满足(其它条件不变)时,请画出图形,并直接写出△ABC与△BDE的面积之比.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
