3.2 用去括号解一元一次方程(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 3.2 用去括号解一元一次方程(第2课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 06:42:27 | ||
图片预览







文档简介
(共23张PPT)
第三章 一元一次方程
3.2 第2课时
利用移项及合并同类项解一元一次方程
随堂演练
课堂小结
获取新知
例题讲解
情景导入
知识回顾
知识回顾
等式两边都加上(或减去)同一个代数式,
所得结果仍是等式.
等式的基本性质2:
等式两边都乘以(或除以)同一个不等于0的数,所得结果仍是等式.
等式的基本性质1:
情景导入
约公元825年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁译本取名为《对消与还原》.
对消,顾名思义,就是将方程中各项成对消除的意思.相当于现代解方程中的“合并同类项”.
“还原”是什么意思呢?
1、设未知数:设这个班有x名学生.
2、找相等关系:这批书的总数是一个定值,表示它的两个等式相等.
3、列方程:
每人分3本,共分出3x本,加上剩余的20本,这批书共 本.
每人分4本,需要 本,减去缺的25本,这批书共 本.
3x+20
4x
4x-25
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
获取新知
3x+20 = 4x-25
3x+20=4x-25
3x+20-4x=4x-25-4x
3x+20-4x=-25
3x+20-4x-20=-25-20
3x-4x=-25-20
(合并同类项)
(利用等式性质1)
(利用等式性质1)
(合并同类项)
思考:怎样解这个方程?它与上节课遇到的方程有何不同?
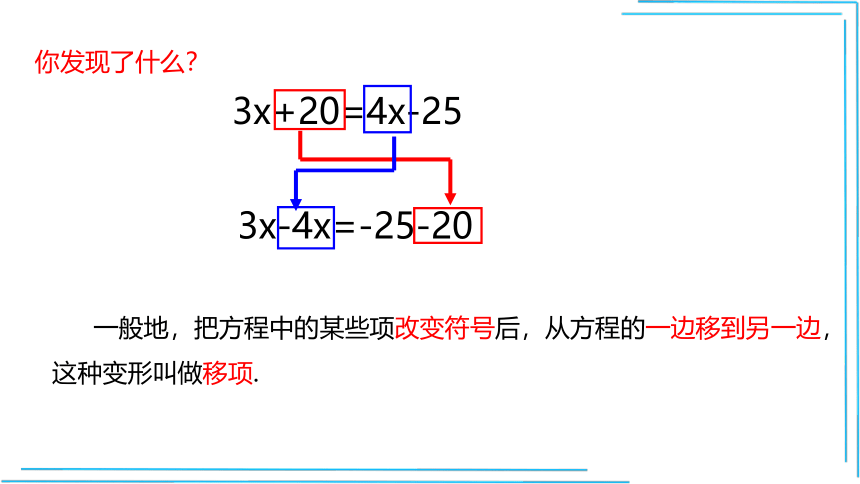
3x+20=4x-25
3x-4x=-25-20
你发现了什么?
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
3x+20=4x-25
3x-4x=-25-20
-x=-45
x=45
移项
合并同类项
系数化为1
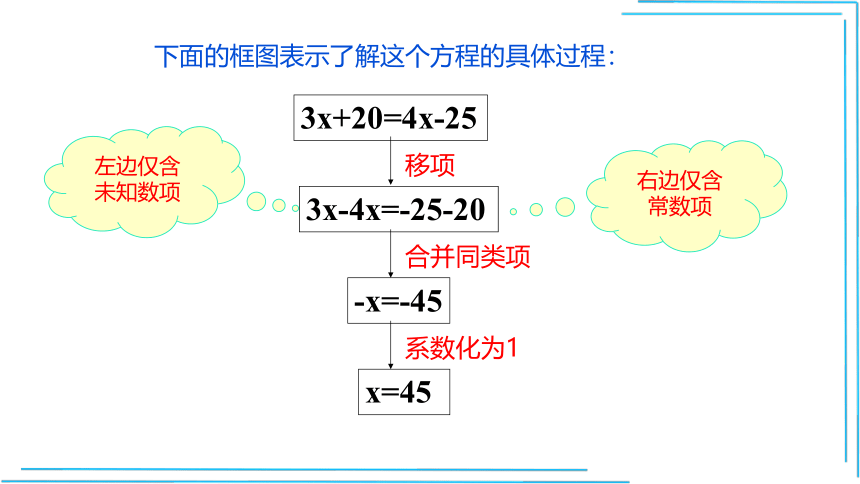
下面的框图表示了解这个方程的具体过程:
左边仅含
未知数项
右边仅含
常数项
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,
目的是便于合并同类项,使方程更接近x=a的形式.
思考2:“移项”起了什么作用?
思考1:以上解方程“移项”的依据是什么?
移项的依据是等式的性质1.
例题讲解
系数化为1,得 x=5.
解:(1)移项,得 3x+2x=32-7.
合并同类项,得 5x=25
例1 解下列方程(1)3x+7=32-2x;
系数化为1,得 x=-8
(2) 移项,得
合并同类项,得
备注:移项时应注意改变项的符号; 步骤为“一移二并三化”
例2 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
思考:(1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?
解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100
移项,得 5x-2x=100+200
合并同类项,得3x=300
系数化为1,得 x=100
所以 2x=200,5x=500.
答:新旧工艺产生的废水数量分别为200 t和500 t.
随堂演练
1. 解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
C
2. 将方程5x+1=2x-3移项后,可得( )
A.5x-2x=-3+1
B.5x-2x=-3-1
C.5x+2x=-3-1
D.5x+2x=1-3
B
3. 方程3x-4=3-2x的解答过程的正确顺序是( )
①合并同类项,得5x=7;
②移项,得3x+2x=3+4;
③系数化为1,得x= .
A.①②③ B.③②①
C.②①③ D.③①②
C
4.下列各式中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
D
5.移项:
(1)由3x+4=1,得3x=________;
(2)由2x+3=-x-6,得________=-6-3.
1-4
2x+x
6.解下列方程:
(1)8y-3=3; (2)2x-19=7x+6;
(3)x-2= x+ ; (4)2x+3=11-6x.
解:(1)移项,得8y=3+3.
合并同类项,得8y=6.
系数化为1,得y= .
(2)移项,得2x-7x=6+19.
合并同类项,得-5x=25.
系数化为1,得x=-5.
(3)移项,得x- x= +2.
合并同类项,得 x= .
系数化为1,得x=5.
(4)移项,得2x+6x=11-3.
合并同类项,得8x=8.
系数化为1,得x=1.
6.解下列方程:
(1)8y-3=3; (2)2x-19=7x+6;
(3)x-2= x+ ; (4)2x+3=11-6x.
7. 列方程解应用题:《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何.”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少.
解:设买羊的人数为x,则羊价为(5x+45)元.
根据题意,得5x+45=7x+3.
解得x=21.
5x+45=5×21+45=150.
答:买羊的人数为21,羊价为150元.
课堂小结
移项解一元一次方程
定义
步骤
应用
注意:移项一定要变号
移项
合并同类项
系数化为1
https://www.21cnjy.com/help/help_extract.php
第三章 一元一次方程
3.2 第2课时
利用移项及合并同类项解一元一次方程
随堂演练
课堂小结
获取新知
例题讲解
情景导入
知识回顾
知识回顾
等式两边都加上(或减去)同一个代数式,
所得结果仍是等式.
等式的基本性质2:
等式两边都乘以(或除以)同一个不等于0的数,所得结果仍是等式.
等式的基本性质1:
情景导入
约公元825年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁译本取名为《对消与还原》.
对消,顾名思义,就是将方程中各项成对消除的意思.相当于现代解方程中的“合并同类项”.
“还原”是什么意思呢?
1、设未知数:设这个班有x名学生.
2、找相等关系:这批书的总数是一个定值,表示它的两个等式相等.
3、列方程:
每人分3本,共分出3x本,加上剩余的20本,这批书共 本.
每人分4本,需要 本,减去缺的25本,这批书共 本.
3x+20
4x
4x-25
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
获取新知
3x+20 = 4x-25
3x+20=4x-25
3x+20-4x=4x-25-4x
3x+20-4x=-25
3x+20-4x-20=-25-20
3x-4x=-25-20
(合并同类项)
(利用等式性质1)
(利用等式性质1)
(合并同类项)
思考:怎样解这个方程?它与上节课遇到的方程有何不同?
3x+20=4x-25
3x-4x=-25-20
你发现了什么?
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
3x+20=4x-25
3x-4x=-25-20
-x=-45
x=45
移项
合并同类项
系数化为1
下面的框图表示了解这个方程的具体过程:
左边仅含
未知数项
右边仅含
常数项
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,
目的是便于合并同类项,使方程更接近x=a的形式.
思考2:“移项”起了什么作用?
思考1:以上解方程“移项”的依据是什么?
移项的依据是等式的性质1.
例题讲解
系数化为1,得 x=5.
解:(1)移项,得 3x+2x=32-7.
合并同类项,得 5x=25
例1 解下列方程(1)3x+7=32-2x;
系数化为1,得 x=-8
(2) 移项,得
合并同类项,得
备注:移项时应注意改变项的符号; 步骤为“一移二并三化”
例2 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
思考:(1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?
解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100
移项,得 5x-2x=100+200
合并同类项,得3x=300
系数化为1,得 x=100
所以 2x=200,5x=500.
答:新旧工艺产生的废水数量分别为200 t和500 t.
随堂演练
1. 解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
C
2. 将方程5x+1=2x-3移项后,可得( )
A.5x-2x=-3+1
B.5x-2x=-3-1
C.5x+2x=-3-1
D.5x+2x=1-3
B
3. 方程3x-4=3-2x的解答过程的正确顺序是( )
①合并同类项,得5x=7;
②移项,得3x+2x=3+4;
③系数化为1,得x= .
A.①②③ B.③②①
C.②①③ D.③①②
C
4.下列各式中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
D
5.移项:
(1)由3x+4=1,得3x=________;
(2)由2x+3=-x-6,得________=-6-3.
1-4
2x+x
6.解下列方程:
(1)8y-3=3; (2)2x-19=7x+6;
(3)x-2= x+ ; (4)2x+3=11-6x.
解:(1)移项,得8y=3+3.
合并同类项,得8y=6.
系数化为1,得y= .
(2)移项,得2x-7x=6+19.
合并同类项,得-5x=25.
系数化为1,得x=-5.
(3)移项,得x- x= +2.
合并同类项,得 x= .
系数化为1,得x=5.
(4)移项,得2x+6x=11-3.
合并同类项,得8x=8.
系数化为1,得x=1.
6.解下列方程:
(1)8y-3=3; (2)2x-19=7x+6;
(3)x-2= x+ ; (4)2x+3=11-6x.
7. 列方程解应用题:《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何.”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少.
解:设买羊的人数为x,则羊价为(5x+45)元.
根据题意,得5x+45=7x+3.
解得x=21.
5x+45=5×21+45=150.
答:买羊的人数为21,羊价为150元.
课堂小结
移项解一元一次方程
定义
步骤
应用
注意:移项一定要变号
移项
合并同类项
系数化为1
https://www.21cnjy.com/help/help_extract.php
