12.1全等三角形同步能力达标测评 2021-2022学年人教版八年级数学上册 (Word版 含答案)
文档属性
| 名称 | 12.1全等三角形同步能力达标测评 2021-2022学年人教版八年级数学上册 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 182.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 12:14:30 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学上册《12.1全等三角形》同步能力达标测评(附答案)
一.选择题(共7小题,满分35分)
1.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
2.如图,△ABC≌△EFD,则下列说法错误的是( )
A.FC=BD B.EF平行且等于AB
C.AC平行且等于DE D.CD=ED
3.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
4.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20° B.25° C.30° D.35°
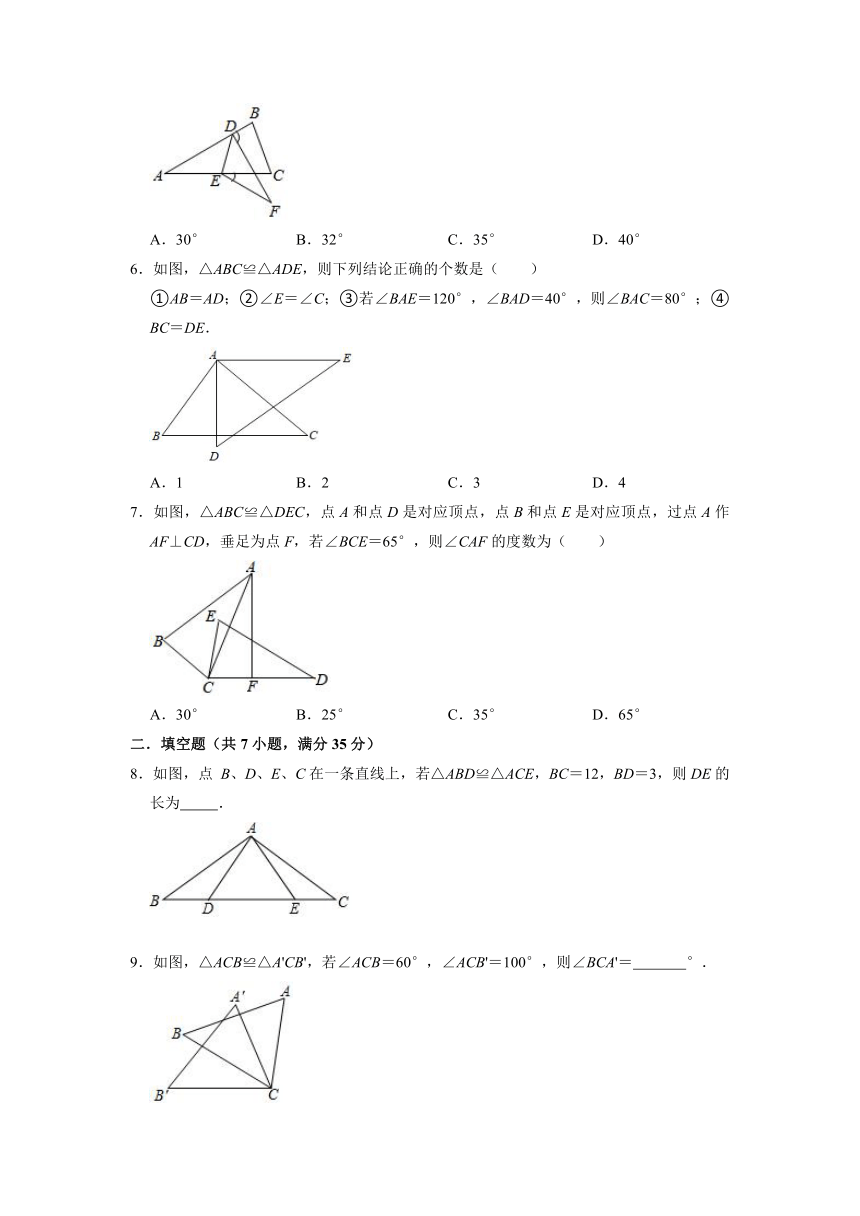
5.如图,点D、E分别在△ABC的边AB、AC上,且△DEF≌△DEA,若∠BDF﹣∠CEF=60°,则∠A的度数为( )
A.30° B.32° C.35° D.40°
6.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1 B.2 C.3 D.4
7.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
二.填空题(共7小题,满分35分)
8.如图,点 B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为 .
9.如图,△ACB≌△A'CB',若∠ACB=60°,∠ACB'=100°,则∠BCA'= °.
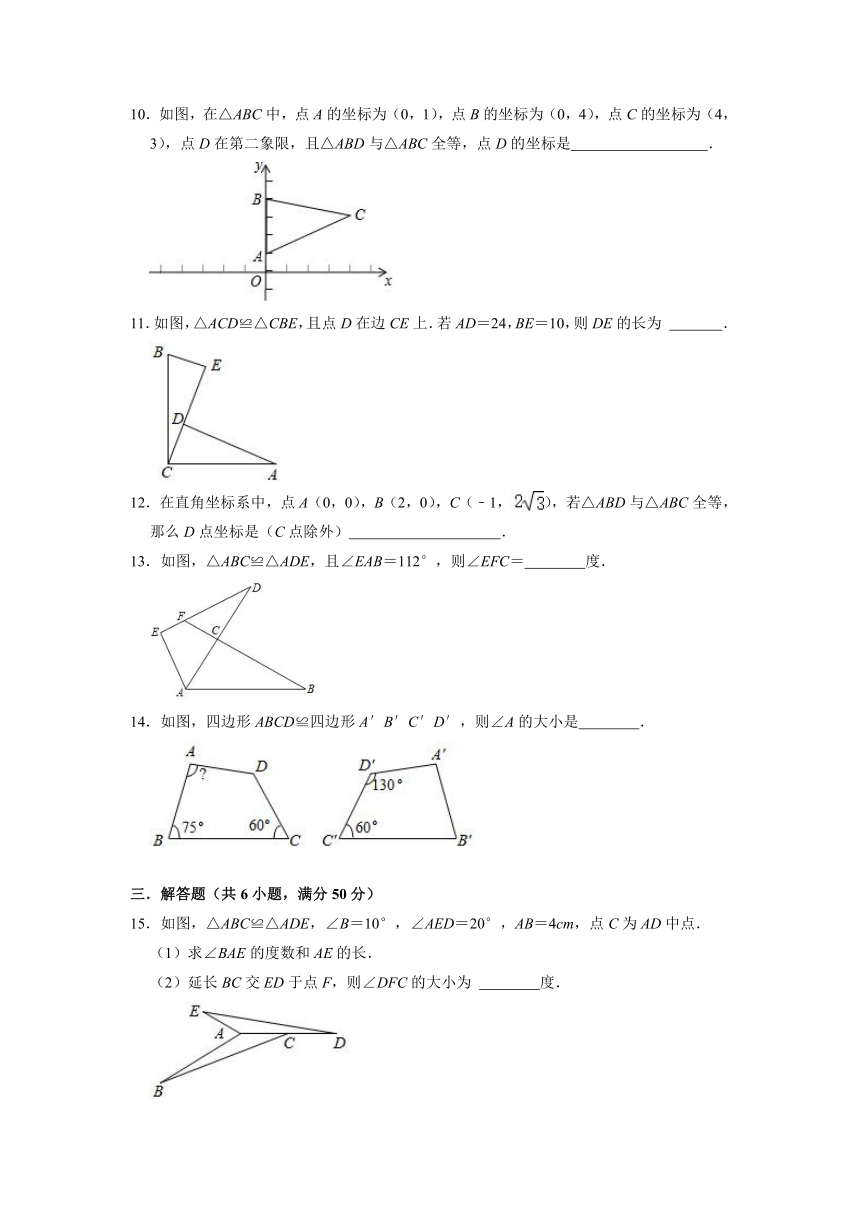
10.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限,且△ABD与△ABC全等,点D的坐标是 .
11.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
12.在直角坐标系中,点A(0,0),B(2,0),C(﹣1,),若△ABD与△ABC全等,那么D点坐标是(C点除外) .
13.如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC= 度.
14.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .
三.解答题(共6小题,满分50分)
15.如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.
(1)求∠BAE的度数和AE的长.
(2)延长BC交ED于点F,则∠DFC的大小为 度.
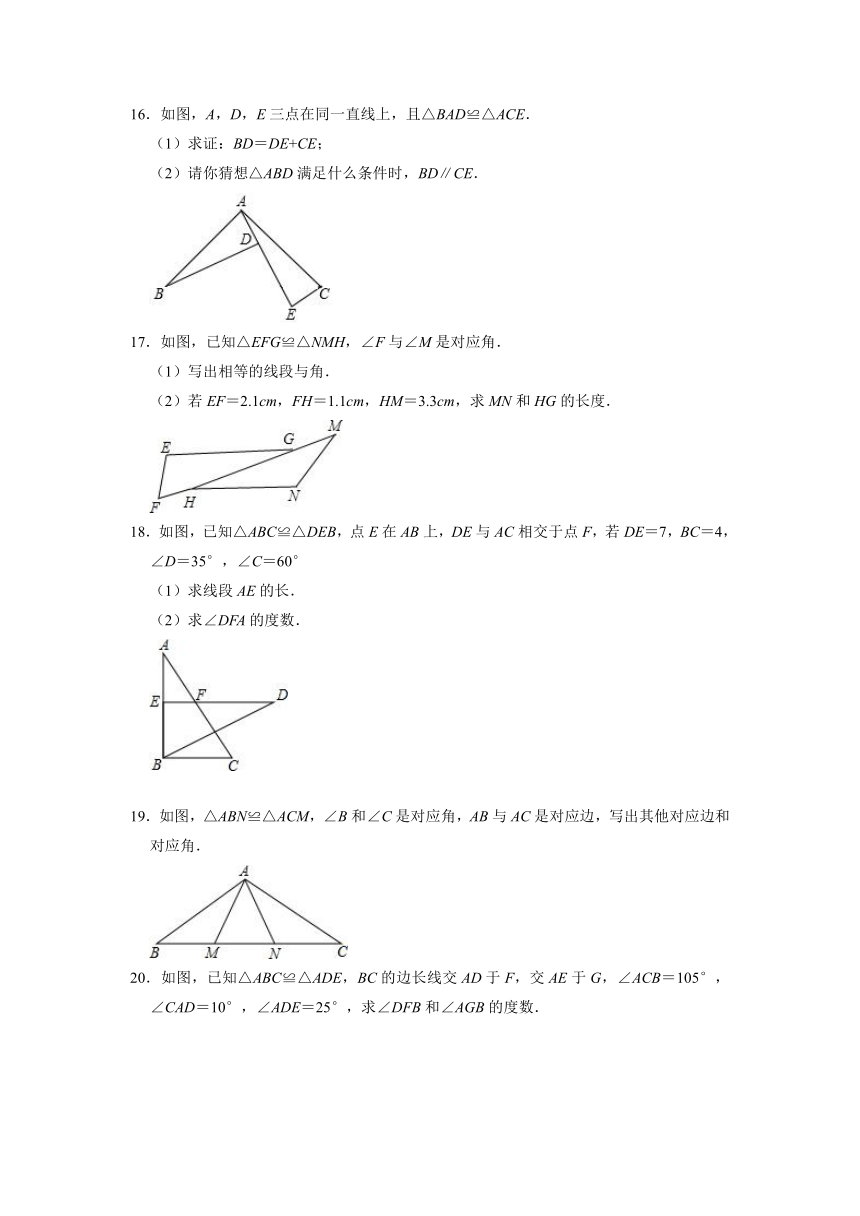
16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
17.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出相等的线段与角.
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
18.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°
(1)求线段AE的长.
(2)求∠DFA的度数.
19.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
20.如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
参考答案
一.选择题(共7小题,满分35分)
1.解:∵△ABC≌△DEC,
∴AC=DC,CB=CE,
∵CE=5,AC=7,
∴CB=5,DC=7,
∴BD=DC+CB=7+5=12.
故选:A.
2.解:A、∵△ABC≌△EFD,
∴FD=CB,
∴FD﹣CD=BC﹣CD,
即FC=BD,故此选项不合题意;
B、∵△ABC≌△EFD,
∴∠F=∠B,EF=AB,
∴EF∥AB,故此选项不合题意;
C、∵△ABC≌△EFD,
∴AC∥DE,AC=DE,故此选项不合题意;
D、不能证明CD=ED,故此选项符合题意;
故选:D.
3.解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
4.解:∵△ABC≌△DBE,∠ABC=80°,
∴∠DBE=∠ABC=80°,
∵∠D=65°,
∴∠C=180°﹣∠DBE﹣∠D=35°,
故选:D.
5.解:∵△DEF≌△DEA,
∴∠F=∠A,
∵∠BDF=∠A+∠1,∠1=∠CEF+∠F,
∴∠1=∠CEF+∠A,
∴∠BDF=∠A+∠CEF+∠A,
∴2∠A=∠BDF﹣∠CEF=60°,
∴∠A=30°,
故选:A.
6.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
7.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
二.填空题(共7小题,满分35分)
8.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
9.解:∵△ACB≌△A'CB',
∴∠A′CB′=∠ACB=60°,
∵∠ACB'=100°,
∴∠ACA′=∠ACB′﹣∠ACB=100°﹣60°=40°,
∴∠BCA′=∠ACB﹣∠ACA′=60°﹣40°=20°.
故答案为:20.
10.解:当△ABD≌△ABC时,△ABD和△ABC关于y轴对称,
∴点D的坐标是(﹣4,3),
当△ABD′≌△BAC时,△ABD′的高D′G=△BAC的高CH=4,AG=BH=1,
∴OG=2,
∴点D′的坐标是(﹣4,2),
故答案为:(﹣4,3)或(﹣4,2).
11.解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
故答案为:14.
12.解:当△ABD与△ABC全等,D点在第三象限时,D点坐标是(﹣1,﹣2),
D′点在第一象限时,D′点坐标是(3,2),
D′′点在第四象限时,D′′点坐标是(3,﹣2),
故答案为:(﹣1,﹣2)或(3,2)或(3,﹣2).
13.解:∵△ABC≌△ADE,∠EAB=112°,
∴∠EAD=DAB=56°,∠D=∠B,
∴∠ACB+∠B=180°﹣56°=124°,
∵∠ACB=∠FCD,
∴∠FCD+∠D=124°,
∵∠EFC是△FCD的一个外角,
∴∠EFC=∠FCD+∠D=124°,
故答案为:124.
14.解:∵四边形ABCD≌四边形A'B'C'D',
∴∠D=∠D′=130°,
∴∠A=360°﹣∠B﹣∠C﹣∠D=360°﹣75°﹣60°﹣130°=95°,
故答案为:95°.
三.解答题(共6小题,满分50分)
15.解:(1)∵△ABC≌△ADE,∠B=10°,AB=4cm,
∴∠ADE=∠B=10°,∠EAD=∠CAB,AD=AB=4cm,
∵∠AED=20°,
∴∠EAD=180°﹣∠EAD﹣∠AED=180°﹣10°﹣20°=150°,
∴∠CAB=150°,
∴∠EAB=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC=AD=×4=2(cm),
∴AE=2cm;
(2)∵∠B=10°,∠CAB=150°,
∴∠ACB=180°﹣150°﹣10°=20°,
∴∠FCD=20°,
∴∠DFC=180°﹣20°﹣10°=150°,
故答案为:150.
16.(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:假如BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
17.解:(1)∵△EFG≌△NMH,∠F与∠M是对应角,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm.
18.解:(1)∵△ABC≌△DEB,
∴AB=DE=7,BE=BC=4,
∴AE=AB﹣BE=7﹣4=3;
(2)∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°,
∴∠DFA=∠A+∠AEF=∠A+∠D+∠DBE=130°.
19.解:∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,
∴对应边:AN与AM,BN与CM;
对应角:∠BAN=∠CAM,∠ANB=∠AMC.
20.解:∵△ABC≌△ADE,
∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.
∵∠ADE=25°,
∴∠ABC=∠ADE=25°.
∵∠ACB=105°,
∴∠CAB=180°﹣105°﹣25°=50°.
∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°.
∠AGB=∠ACB﹣∠GAC=105°﹣50°﹣10°=45°
一.选择题(共7小题,满分35分)
1.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
2.如图,△ABC≌△EFD,则下列说法错误的是( )
A.FC=BD B.EF平行且等于AB
C.AC平行且等于DE D.CD=ED
3.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
4.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20° B.25° C.30° D.35°
5.如图,点D、E分别在△ABC的边AB、AC上,且△DEF≌△DEA,若∠BDF﹣∠CEF=60°,则∠A的度数为( )
A.30° B.32° C.35° D.40°
6.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1 B.2 C.3 D.4
7.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
二.填空题(共7小题,满分35分)
8.如图,点 B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为 .
9.如图,△ACB≌△A'CB',若∠ACB=60°,∠ACB'=100°,则∠BCA'= °.
10.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限,且△ABD与△ABC全等,点D的坐标是 .
11.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
12.在直角坐标系中,点A(0,0),B(2,0),C(﹣1,),若△ABD与△ABC全等,那么D点坐标是(C点除外) .
13.如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC= 度.
14.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .
三.解答题(共6小题,满分50分)
15.如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.
(1)求∠BAE的度数和AE的长.
(2)延长BC交ED于点F,则∠DFC的大小为 度.
16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
17.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出相等的线段与角.
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
18.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°
(1)求线段AE的长.
(2)求∠DFA的度数.
19.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
20.如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
参考答案
一.选择题(共7小题,满分35分)
1.解:∵△ABC≌△DEC,
∴AC=DC,CB=CE,
∵CE=5,AC=7,
∴CB=5,DC=7,
∴BD=DC+CB=7+5=12.
故选:A.
2.解:A、∵△ABC≌△EFD,
∴FD=CB,
∴FD﹣CD=BC﹣CD,
即FC=BD,故此选项不合题意;
B、∵△ABC≌△EFD,
∴∠F=∠B,EF=AB,
∴EF∥AB,故此选项不合题意;
C、∵△ABC≌△EFD,
∴AC∥DE,AC=DE,故此选项不合题意;
D、不能证明CD=ED,故此选项符合题意;
故选:D.
3.解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
4.解:∵△ABC≌△DBE,∠ABC=80°,
∴∠DBE=∠ABC=80°,
∵∠D=65°,
∴∠C=180°﹣∠DBE﹣∠D=35°,
故选:D.
5.解:∵△DEF≌△DEA,
∴∠F=∠A,
∵∠BDF=∠A+∠1,∠1=∠CEF+∠F,
∴∠1=∠CEF+∠A,
∴∠BDF=∠A+∠CEF+∠A,
∴2∠A=∠BDF﹣∠CEF=60°,
∴∠A=30°,
故选:A.
6.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
7.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
二.填空题(共7小题,满分35分)
8.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
9.解:∵△ACB≌△A'CB',
∴∠A′CB′=∠ACB=60°,
∵∠ACB'=100°,
∴∠ACA′=∠ACB′﹣∠ACB=100°﹣60°=40°,
∴∠BCA′=∠ACB﹣∠ACA′=60°﹣40°=20°.
故答案为:20.
10.解:当△ABD≌△ABC时,△ABD和△ABC关于y轴对称,
∴点D的坐标是(﹣4,3),
当△ABD′≌△BAC时,△ABD′的高D′G=△BAC的高CH=4,AG=BH=1,
∴OG=2,
∴点D′的坐标是(﹣4,2),
故答案为:(﹣4,3)或(﹣4,2).
11.解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
故答案为:14.
12.解:当△ABD与△ABC全等,D点在第三象限时,D点坐标是(﹣1,﹣2),
D′点在第一象限时,D′点坐标是(3,2),
D′′点在第四象限时,D′′点坐标是(3,﹣2),
故答案为:(﹣1,﹣2)或(3,2)或(3,﹣2).
13.解:∵△ABC≌△ADE,∠EAB=112°,
∴∠EAD=DAB=56°,∠D=∠B,
∴∠ACB+∠B=180°﹣56°=124°,
∵∠ACB=∠FCD,
∴∠FCD+∠D=124°,
∵∠EFC是△FCD的一个外角,
∴∠EFC=∠FCD+∠D=124°,
故答案为:124.
14.解:∵四边形ABCD≌四边形A'B'C'D',
∴∠D=∠D′=130°,
∴∠A=360°﹣∠B﹣∠C﹣∠D=360°﹣75°﹣60°﹣130°=95°,
故答案为:95°.
三.解答题(共6小题,满分50分)
15.解:(1)∵△ABC≌△ADE,∠B=10°,AB=4cm,
∴∠ADE=∠B=10°,∠EAD=∠CAB,AD=AB=4cm,
∵∠AED=20°,
∴∠EAD=180°﹣∠EAD﹣∠AED=180°﹣10°﹣20°=150°,
∴∠CAB=150°,
∴∠EAB=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC=AD=×4=2(cm),
∴AE=2cm;
(2)∵∠B=10°,∠CAB=150°,
∴∠ACB=180°﹣150°﹣10°=20°,
∴∠FCD=20°,
∴∠DFC=180°﹣20°﹣10°=150°,
故答案为:150.
16.(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:假如BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
17.解:(1)∵△EFG≌△NMH,∠F与∠M是对应角,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm.
18.解:(1)∵△ABC≌△DEB,
∴AB=DE=7,BE=BC=4,
∴AE=AB﹣BE=7﹣4=3;
(2)∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°,
∴∠DFA=∠A+∠AEF=∠A+∠D+∠DBE=130°.
19.解:∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,
∴对应边:AN与AM,BN与CM;
对应角:∠BAN=∠CAM,∠ANB=∠AMC.
20.解:∵△ABC≌△ADE,
∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.
∵∠ADE=25°,
∴∠ABC=∠ADE=25°.
∵∠ACB=105°,
∴∠CAB=180°﹣105°﹣25°=50°.
∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°.
∠AGB=∠ACB﹣∠GAC=105°﹣50°﹣10°=45°
