23.2.2 中心对称图形(附答案)【人教九上数学学霸提升作业】
文档属性
| 名称 | 23.2.2 中心对称图形(附答案)【人教九上数学学霸提升作业】 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 10:07:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
23.2.2 中心对称图形
命题点 1 识别轴对称图形与中心对称图形
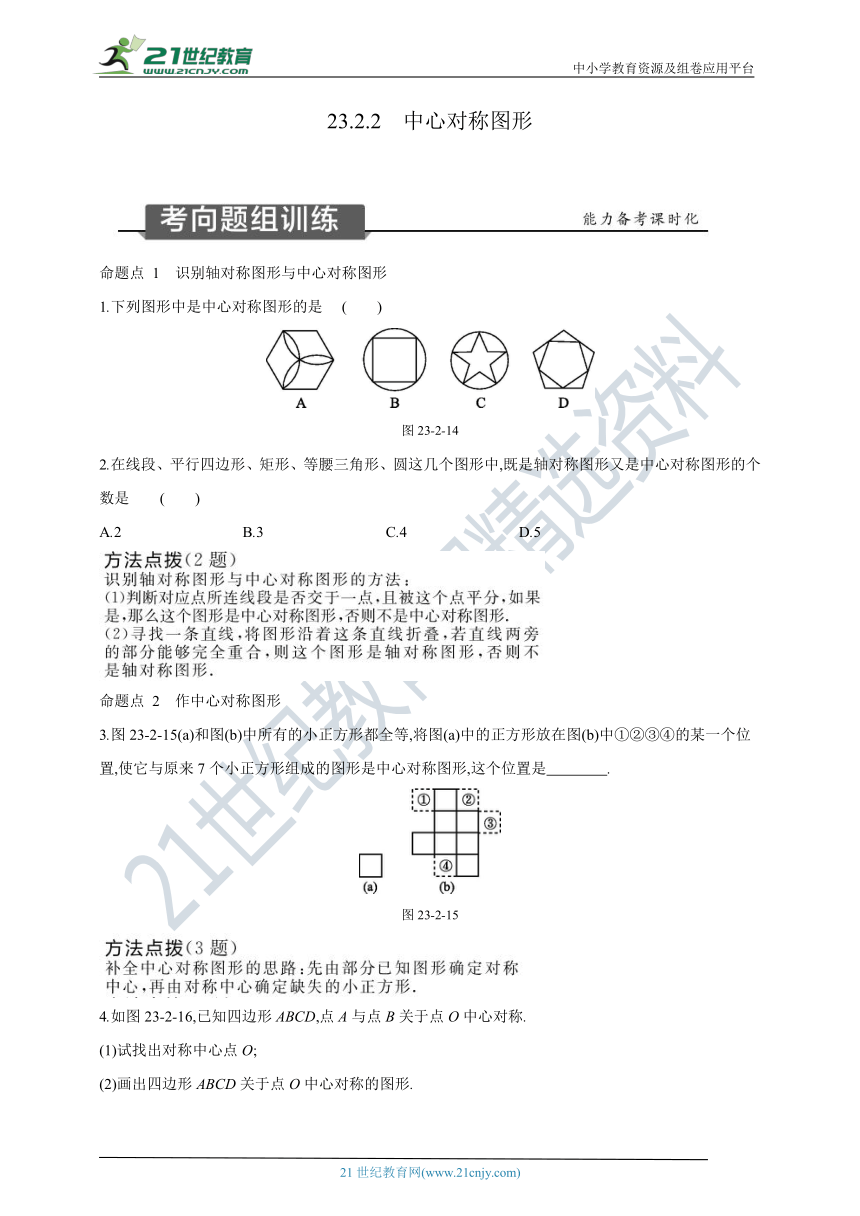
1.下列图形中是中心对称图形的是 ( )
图23-2-14
2.在线段、平行四边形、矩形、等腰三角形、圆这几个图形中,既是轴对称图形又是中心对称图形的个数是 ( )
A.2 B.3 C.4 D.5
命题点 2 作中心对称图形
3.图23-2-15(a)和图(b)中所有的小正方形都全等,将图(a)中的正方形放在图(b)中①②③④的某一个位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 .
图23-2-15
4.如图23-2-16,已知四边形ABCD,点A与点B关于点O中心对称.
(1)试找出对称中心点O;
(2)画出四边形ABCD关于点O中心对称的图形.
图23-2-16
命题点 3 中心对称图形的性质与判定
5.在一次游戏当中,小明将图23-2-17中的四张扑克牌中的三张旋转了180°,得到的四张牌的图案和原来的一模一样,小芳看了后,很快就知道没有旋转的那张扑克牌是 ( )
图23-2-17
A.黑桃Q B.梅花2 C.梅花6 D.方块9
6.如图23-2-18所示,EF过矩形ABCD对角线的交点O,且与AB,CD分别交于点E,F,若AB=3,BC=4,则阴影部分的面积为 ( )
A.12 B.6 C.4 D.3
图23-2-18 图23-2-19
7.如图23-2-19,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C中心对称,则AE的长是 .
8.如图23-2-20,在平行四边形ABCD中,AB=4,BC=3,O是平行四边形ABCD的对称中心,O'是菱形ABEF的对称中心,若OO'=d,则d的取值范围是 .
图23-2-20
9.图23-2-21①②均为7×6的正方形网格,点A,B,C在格点(小正方形的顶点)上.
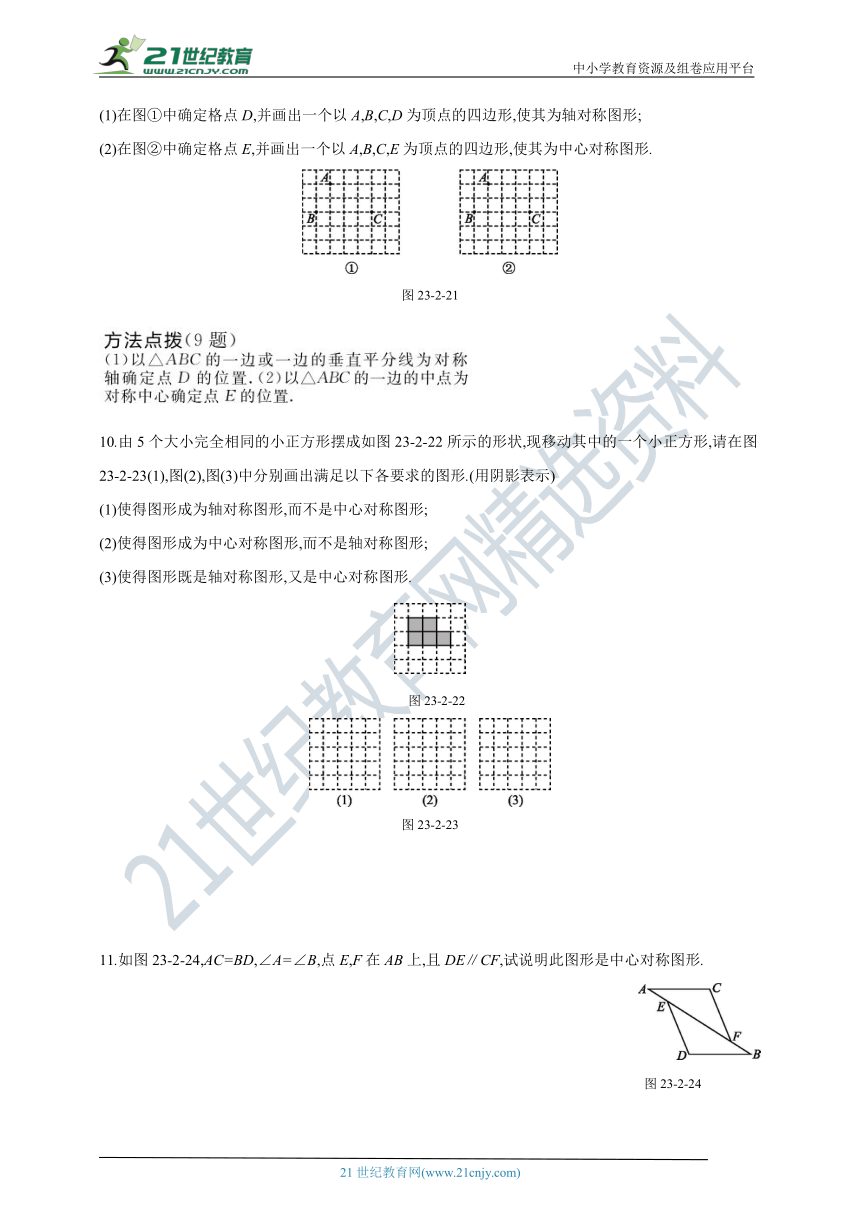
(1)在图①中确定格点D,并画出一个以A,B,C,D为顶点的四边形,使其为轴对称图形;
(2)在图②中确定格点E,并画出一个以A,B,C,E为顶点的四边形,使其为中心对称图形.
图23-2-21
10.由5个大小完全相同的小正方形摆成如图23-2-22所示的形状,现移动其中的一个小正方形,请在图23-2-23(1),图(2),图(3)中分别画出满足以下各要求的图形.(用阴影表示)
(1)使得图形成为轴对称图形,而不是中心对称图形;
(2)使得图形成为中心对称图形,而不是轴对称图形;
(3)使得图形既是轴对称图形,又是中心对称图形.
图23-2-22
图23-2-23
11.如图23-2-24,AC=BD,∠A=∠B,点E,F在AB上,且DE∥CF,试说明此图形是中心对称图形.
图23-2-24
12.知识背景:过中心对称图形的对称中心的任意一条直线都将该图形分成全等的两部分.
(1)如图23-2-25①,直线m经过 ABCD对角线的交点O,则S四边形BFEA S四边形DEFC(填“>”“<”或“=”);
(2)两个正方形如图②所示摆放,O为小正方形对角线的交点,求作过点O的直线,使其将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线,使其将整个图形分成面积相等的两部分(用三种方法分割).
图23-2-25
13.如图23-2-26,矩形ABCD的顶点B,C在x轴上,顶点D的坐标是(3,3),若直线y=mx恰好将矩形分成面积相等的两部分,求m的值.
图23-2-26
典题讲评与答案详析
1.B
2.B [解析] 线段、矩形、圆既是轴对称图形,又是中心对称图形,平行四边形是中心对称图形,不是轴对称图形,等腰三角形是轴对称图形,不是中心对称图形.故选B.
3.③
4.解:(1)如图,点O即为所求.
(2)如图,四边形A'B'C'D'即为所求.
5.C [解析] 四张扑克牌中只有梅花6不是中心对称图形.把梅花6旋转180°,会和原来的图案不一样,而本题中得到的图案和原来的一模一样,因此只有梅花6没有旋转.
6.D [解析] ∵四边形ABCD是矩形,O是对角线的交点,∴△DOF与△BOE关于点O中心对称,
∴S△DOF=S△BOE,
∴阴影部分的面积为△AOB的面积.
∵S△AOB=S矩形ABCD=3,∴S阴影=3.
7. [解析] ∵△DEC与△ABC关于点C中心对称,
∴DC=AC=1,DE=AB=3,
∴在Rt△EDA中,AE的长是=.
故答案为.
8.0.5≤d≤3.5 [解析] 如图,连接AC,AE,EC,OO'.
∵O是平行四边形ABCD的对称中心,O'是菱形ABEF的对称中心,∴CO=AO,AO'=EO',
∴OO'=EC.∵BC=3,BE=AB=4,
∴1≤EC≤7,∴0.5≤OO'≤3.5,即0.5≤d≤3.5.
9.解:(1)答案不唯一,有以下答案供参考:
(2)答案不唯一,有以下答案供参考:
10.解:(1)如图所示(答案不唯一):
(2)如图所示:
(3)如图所示:
11.解:如图,连接CD,交AB于点O.
在△ACO和△BDO中,
∴△ACO≌△BDO(AAS),
∴OA=OB,OC=OD.
∵DE∥CF,∴∠DEO=∠CFO.
在△ODE和△OCF中,
∴△ODE≌△OCF(AAS),
∴OE=OF,
∴此图形是中心对称图形.
12.解:(1)=
(2)如图所示.
(3)如图所示.
13.解:∵直线y=mx恰好将矩形分成面积相等的两部分,且矩形ABCD是中心对称图形,
∴该直线过矩形的对称中心,即矩形对角线的交点.
对角线交点的横坐标即线段BC的中点对应的横坐标,对角线交点的纵坐标即线段DC的中点对应的纵坐标,由题图可知,对角线交点的坐标为1,.
∵直线y=mx过点1,,∴=1×m,
∴m=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
23.2.2 中心对称图形
命题点 1 识别轴对称图形与中心对称图形
1.下列图形中是中心对称图形的是 ( )
图23-2-14
2.在线段、平行四边形、矩形、等腰三角形、圆这几个图形中,既是轴对称图形又是中心对称图形的个数是 ( )
A.2 B.3 C.4 D.5
命题点 2 作中心对称图形
3.图23-2-15(a)和图(b)中所有的小正方形都全等,将图(a)中的正方形放在图(b)中①②③④的某一个位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 .
图23-2-15
4.如图23-2-16,已知四边形ABCD,点A与点B关于点O中心对称.
(1)试找出对称中心点O;
(2)画出四边形ABCD关于点O中心对称的图形.
图23-2-16
命题点 3 中心对称图形的性质与判定
5.在一次游戏当中,小明将图23-2-17中的四张扑克牌中的三张旋转了180°,得到的四张牌的图案和原来的一模一样,小芳看了后,很快就知道没有旋转的那张扑克牌是 ( )
图23-2-17
A.黑桃Q B.梅花2 C.梅花6 D.方块9
6.如图23-2-18所示,EF过矩形ABCD对角线的交点O,且与AB,CD分别交于点E,F,若AB=3,BC=4,则阴影部分的面积为 ( )
A.12 B.6 C.4 D.3
图23-2-18 图23-2-19
7.如图23-2-19,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C中心对称,则AE的长是 .
8.如图23-2-20,在平行四边形ABCD中,AB=4,BC=3,O是平行四边形ABCD的对称中心,O'是菱形ABEF的对称中心,若OO'=d,则d的取值范围是 .
图23-2-20
9.图23-2-21①②均为7×6的正方形网格,点A,B,C在格点(小正方形的顶点)上.
(1)在图①中确定格点D,并画出一个以A,B,C,D为顶点的四边形,使其为轴对称图形;
(2)在图②中确定格点E,并画出一个以A,B,C,E为顶点的四边形,使其为中心对称图形.
图23-2-21
10.由5个大小完全相同的小正方形摆成如图23-2-22所示的形状,现移动其中的一个小正方形,请在图23-2-23(1),图(2),图(3)中分别画出满足以下各要求的图形.(用阴影表示)
(1)使得图形成为轴对称图形,而不是中心对称图形;
(2)使得图形成为中心对称图形,而不是轴对称图形;
(3)使得图形既是轴对称图形,又是中心对称图形.
图23-2-22
图23-2-23
11.如图23-2-24,AC=BD,∠A=∠B,点E,F在AB上,且DE∥CF,试说明此图形是中心对称图形.
图23-2-24
12.知识背景:过中心对称图形的对称中心的任意一条直线都将该图形分成全等的两部分.
(1)如图23-2-25①,直线m经过 ABCD对角线的交点O,则S四边形BFEA S四边形DEFC(填“>”“<”或“=”);
(2)两个正方形如图②所示摆放,O为小正方形对角线的交点,求作过点O的直线,使其将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线,使其将整个图形分成面积相等的两部分(用三种方法分割).
图23-2-25
13.如图23-2-26,矩形ABCD的顶点B,C在x轴上,顶点D的坐标是(3,3),若直线y=mx恰好将矩形分成面积相等的两部分,求m的值.
图23-2-26
典题讲评与答案详析
1.B
2.B [解析] 线段、矩形、圆既是轴对称图形,又是中心对称图形,平行四边形是中心对称图形,不是轴对称图形,等腰三角形是轴对称图形,不是中心对称图形.故选B.
3.③
4.解:(1)如图,点O即为所求.
(2)如图,四边形A'B'C'D'即为所求.
5.C [解析] 四张扑克牌中只有梅花6不是中心对称图形.把梅花6旋转180°,会和原来的图案不一样,而本题中得到的图案和原来的一模一样,因此只有梅花6没有旋转.
6.D [解析] ∵四边形ABCD是矩形,O是对角线的交点,∴△DOF与△BOE关于点O中心对称,
∴S△DOF=S△BOE,
∴阴影部分的面积为△AOB的面积.
∵S△AOB=S矩形ABCD=3,∴S阴影=3.
7. [解析] ∵△DEC与△ABC关于点C中心对称,
∴DC=AC=1,DE=AB=3,
∴在Rt△EDA中,AE的长是=.
故答案为.
8.0.5≤d≤3.5 [解析] 如图,连接AC,AE,EC,OO'.
∵O是平行四边形ABCD的对称中心,O'是菱形ABEF的对称中心,∴CO=AO,AO'=EO',
∴OO'=EC.∵BC=3,BE=AB=4,
∴1≤EC≤7,∴0.5≤OO'≤3.5,即0.5≤d≤3.5.
9.解:(1)答案不唯一,有以下答案供参考:
(2)答案不唯一,有以下答案供参考:
10.解:(1)如图所示(答案不唯一):
(2)如图所示:
(3)如图所示:
11.解:如图,连接CD,交AB于点O.
在△ACO和△BDO中,
∴△ACO≌△BDO(AAS),
∴OA=OB,OC=OD.
∵DE∥CF,∴∠DEO=∠CFO.
在△ODE和△OCF中,
∴△ODE≌△OCF(AAS),
∴OE=OF,
∴此图形是中心对称图形.
12.解:(1)=
(2)如图所示.
(3)如图所示.
13.解:∵直线y=mx恰好将矩形分成面积相等的两部分,且矩形ABCD是中心对称图形,
∴该直线过矩形的对称中心,即矩形对角线的交点.
对角线交点的横坐标即线段BC的中点对应的横坐标,对角线交点的纵坐标即线段DC的中点对应的纵坐标,由题图可知,对角线交点的坐标为1,.
∵直线y=mx过点1,,∴=1×m,
∴m=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
