分式复习
图片预览









文档简介
(共50张PPT)
1:填空(每空5分)
(1)当x 时, 值为0
(2)当x 时, 值为正数.
=2
>-2且x≠0
3.当 时,则分式 有意义.
4.若分式 的值等于零,则应满足的
条件是 .
2.在代数式
中,分式共有_____个。
3
x=-2
x≠3且x ≠-3
巩固练习
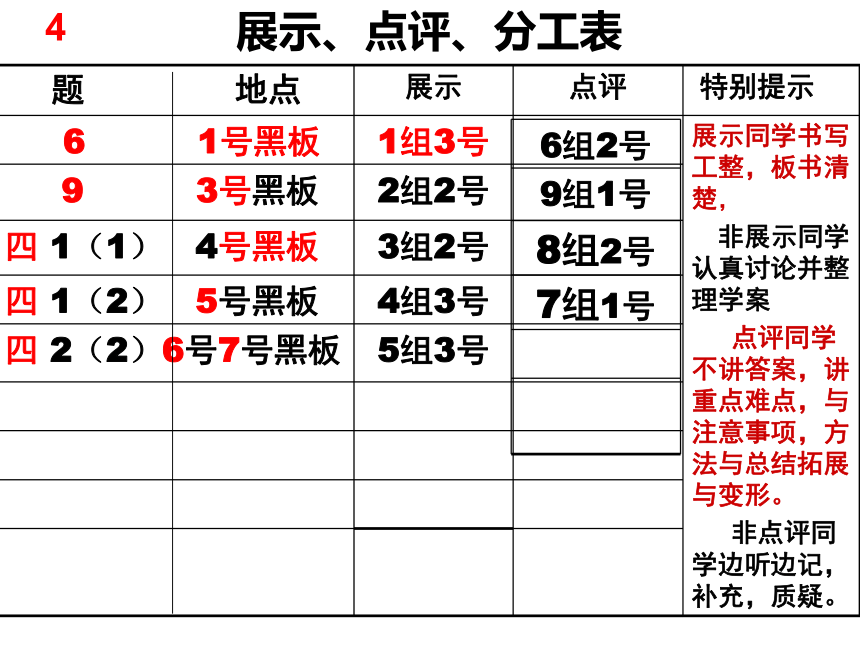
题 地点 展示 点评 特别提示
6 1号黑板 1组3号 展示同学书写工整,板书清楚,
非展示同学认真讨论并整理学案
点评同学不讲答案,讲重点难点,与注意事项,方法与总结拓展与变形。
非点评同学边听边记,补充,质疑。
9 3号黑板 2组2号
四 1(1) 4号黑板 3组2号
四 1(2) 5号黑板 4组3号
四 2(2)6号7号黑板 5组3号
展示、点评、分工表
6组2号
9组1号
8组2号
7组1号
4
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 就叫做分式.
归纳
分式 中,
A叫做分式的分子,B叫做分式的分母.
分式是不同于整式的另一类式子。
分式定义
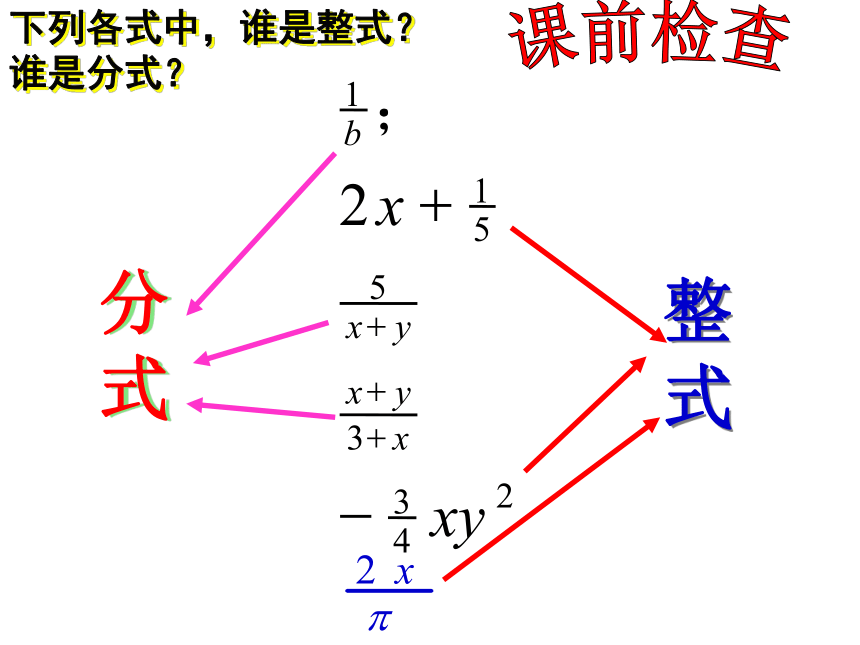
下列各式中,谁是整式?谁是分式?
分式
整
式
2
4
3
3
5
5
1
1
2
xy
x
x
y
x
y
x
b
-
+
+
+
+
;
复习回顾
(1) 下列各式中,属于分式的是( )
A、 B、 C、 D、
B
(2)A、B都是整式,则 一定是分式。
(3)若B含字母,则 一定是分式。
×
×
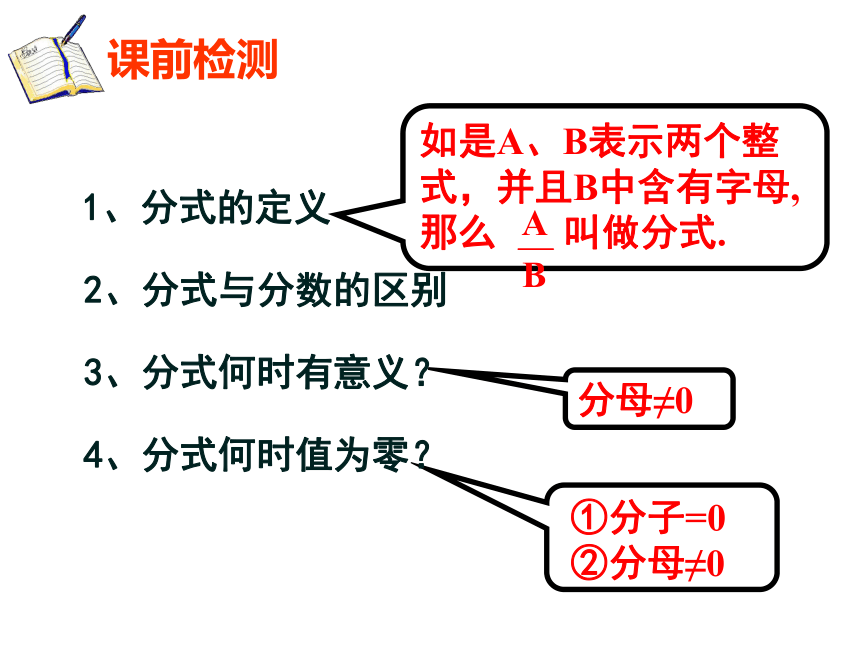
课前检测
分母≠0
①分子=0 ②分母≠0
如是A、B表示两个整式,并且B中含有字母,那么 叫做分式.
1、分式的定义
2、分式与分数的区别
3、分式何时有意义?
4、分式何时值为零?
1:填空(每空5分)
(1)当x 时, 无意义
(2)当x 时, 值为0
(3)当x=1时, 值为_________.
(4)当x 时, 值为正数.
(5)当x=5时,分式 值为零,则k=_______.
=-2
=2
>-2且x≠0
3
-10
化简下列分式(约分)
约分的步骤
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂
(1)
(2)
(3)
把分式分子、分母的 公因式约去,这种变
形叫分式的约分.
分式约分的依据是什么?
分式的基本性质
约分
注意:
当分子分母是多项式的时候,先进行分解因式,再约分
(3)
对于分数而言,彻底约分后的分数叫什么?
在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看!
彻底约分后的分式叫最简分式.
一般约分要彻底, 使分子、分母没有公因式.
(1)
(2)
与
与
解:
(1)最简公分母是
(3)
把各分式化成相同
分母的分式叫做
分式的通分.
绝对值大于10的数记成a×10n的形式,其中1≤︱a︱<10,n是正整数.
例如:864000可以写成8.64×105.
科学记数法:
n等于原数的整数数位减1
我们可以利用10的负整数次幂,用科学记数法表示一些绝对值小于1的数,
即将它们表示成a×10-n的形式.
(其中n是正整数,1≤∣a∣<10.)
类似:
1. a0=1
规定
(其中n为正整数且
例1计算:
练习
1、若(2x-1)0=1,求x的取值范围。
2、下列计算正确的是( )
D
概括:分式方程
分母中含有未知数的方程,叫做分式方程
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
一化二解三检验
解分式方程的一般步骤
分式的基本性质:
分式的分子与分母同时乘以(或除以)同一个不等于零的整式 ,分式的值不变.
练习1. 填空:
.
三、例题讲解与练习
4n
a2+ab
x
不改变分式的值,把下列各式的分子与分母的各项系数都化为整数.
⑴ ⑵
(3)
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。
用符号语言表达:
两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘。
用符号语言表达:
例1 计算:
注意:乘法运算时,分子或分母能分解的要分解.
(1)分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
(2)分子相加减时,如果分子是一个多项式,要将分子看成一个整体,先用括号括起来,再运算,可减少出现符号错误。
(3)分式加减运算的结果要约分,化为最 简分式(或整式)。
练习:用科学记数法表示下列个数
0.000000108
-0.00003
3.
2.
1.
-56700000
4.
6.
-0.0000067
5.
复
习:
正整数指数幂的运算性质:
1)am·an=am+n (a≠0 m、n为正整数)
2)(am)n=amn (a≠0 m、n为正整数)
3)(ab)n=anbn(a,b≠0 m、n为正整数)
4)am÷an=am-n (a≠0 m、n为正整数且 m>n)
5) ( b≠0 ,n是正整数)
当a≠0时,a0=1。(0指数幂的运算)
6)
例1计算:
1、2(x-1)=x+1; x2+x-20=0; x+2y=1…
2、
整式方程:
方程两边都是整式的方程.
分式方程:
分母中含有未知数的方程.
观察下列方程:
概 念
一元一次方程
一元二次方程
解分式方程
化简,得整式方程 2(x-9)=x+9
解整式方程,得 x= 27.
当x=27时, 2(x+9) ≠0
∴ x = 27是原方程的解.
● ● ● ● ●
分式方程
整式方程
解整式方程
检 验
转化
① ② ③
检验:
解: 方程的两边同乘以最简公分母2(x+9),
得,
梳理
(1) 分式是两个整式相除的商,分数线可以理解为除号,并含有括号的作用.
(2) 分式的分子可以含有字母,也可以不含有字母,但分母必须含有字母.
有理式
整式
分式
如何判断一个式 子是否是分式?
2、下列代数式中,哪些是分式
; (2) ; (3) ;
(4) ; (5) ; (6) .
(1)x÷y ;
(2)6000÷ab ;
(3)a÷(b+c) ;
(4)(a-b)÷c ;
(5)(x-y)÷(x+y) ;
练习
1、把下列式子写成分式的形式。
√
√
√
探究
由于字母可以表示不同的数,所以分式比分数更具有一般性。例如,分数 仅表示2÷3的商,而分式 既可以表示2÷3,又可以表示-5÷2,8÷(-9)等。
分式中的分母应满足什么条件?
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义。
例题
当x为何值时,分式 有意义?
解:
要使分式 有意义,
必须
3x≠0
即x≠0
∴当x≠0时,分式 有意义。
例1
(1)当x 时,分式 有意义;
(2)当b 时,分式 有意义;
(3)当x,y满足关系 时,分式
有意义;
例2 填空:
解:
(1)当分母x-1≠0即x≠1时,分式 有
意义;
(2)当分母5-3b≠0即b≠ 时,分式
有意义;
(3)当分母x-y≠0即x≠y时,分式
有意义;
若把题目要求改为:“当 取何值时下列分式无意义?”如何解答?
当x取什么值时,下列分式有意义?
; (2) ;
(3) ; (4) .
练习
(2) 由分母 , 得 .
∴当 时,分式 有意义.
(3)∵x2+1≥0恒成立, .
∴ 取任何实数时,原分式都有意义.
(4) 由分母 ,得 .
∴当 时,原分式有意义.
解:(1) 由分母得 ,
∴当 时,分式 有意义.
分式 在什么条件下值为0?
分式的值为0,需满足的条件是:分子的值等于0且分母值不为0.
仅仅是 就可以了吗?
A=0
且B≠0
当x取什么值时,分式
的值为零?
所以,在x+2=0,并且2x-5≠0时,分式的值为零。
例题
分析:分式的值为0,需满足的条件是:分子的值等于0且分母值不为0.
解:
要使原分式的值为零,必须:
x+2=0, 且2x-5≠0
∴x=-2 , 且x ≠
∴当x=-2 时,原分式值为零。
因为x=-2时,分母2x-5≠0,
1、在下列各分式中,当 等于什么数时,分式的值为0?当 等于什么数时,分式没有意义?
(1) ; (2) .
2、分式 的值能等于0吗?说明理由.
练习
1、形如 且B中含有字母的式子叫做分式。其中B≠0。整式和分式统称为有理式。
(3)分式中,当A=0且B ≠ 0时,分式 的值为零。
2.(1)分式中B≠0时,分式 有意义;
(2)分式中B=0,分式 无意义;
小结
2.当 时,则分式 有意义.
3.若分式 的值等于零,则应满足的
条件是 .
1.在代数式
中,分式共有_____个。
3
x=2
x≠3且x ≠-3
巩固练习
1、当x=-2时,分式
没有
意义,求a。
2、当x=3时,分式
零,求a。
的值为
思考
1:填空(每空5分)
(1)当x 时, 值为0
(2)当x 时, 值为正数.
=2
>-2且x≠0
3.当 时,则分式 有意义.
4.若分式 的值等于零,则应满足的
条件是 .
2.在代数式
中,分式共有_____个。
3
x=-2
x≠3且x ≠-3
巩固练习
题 地点 展示 点评 特别提示
6 1号黑板 1组3号 展示同学书写工整,板书清楚,
非展示同学认真讨论并整理学案
点评同学不讲答案,讲重点难点,与注意事项,方法与总结拓展与变形。
非点评同学边听边记,补充,质疑。
9 3号黑板 2组2号
四 1(1) 4号黑板 3组2号
四 1(2) 5号黑板 4组3号
四 2(2)6号7号黑板 5组3号
展示、点评、分工表
6组2号
9组1号
8组2号
7组1号
4
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 就叫做分式.
归纳
分式 中,
A叫做分式的分子,B叫做分式的分母.
分式是不同于整式的另一类式子。
分式定义
下列各式中,谁是整式?谁是分式?
分式
整
式
2
4
3
3
5
5
1
1
2
xy
x
x
y
x
y
x
b
-
+
+
+
+
;
复习回顾
(1) 下列各式中,属于分式的是( )
A、 B、 C、 D、
B
(2)A、B都是整式,则 一定是分式。
(3)若B含字母,则 一定是分式。
×
×
课前检测
分母≠0
①分子=0 ②分母≠0
如是A、B表示两个整式,并且B中含有字母,那么 叫做分式.
1、分式的定义
2、分式与分数的区别
3、分式何时有意义?
4、分式何时值为零?
1:填空(每空5分)
(1)当x 时, 无意义
(2)当x 时, 值为0
(3)当x=1时, 值为_________.
(4)当x 时, 值为正数.
(5)当x=5时,分式 值为零,则k=_______.
=-2
=2
>-2且x≠0
3
-10
化简下列分式(约分)
约分的步骤
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂
(1)
(2)
(3)
把分式分子、分母的 公因式约去,这种变
形叫分式的约分.
分式约分的依据是什么?
分式的基本性质
约分
注意:
当分子分母是多项式的时候,先进行分解因式,再约分
(3)
对于分数而言,彻底约分后的分数叫什么?
在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看!
彻底约分后的分式叫最简分式.
一般约分要彻底, 使分子、分母没有公因式.
(1)
(2)
与
与
解:
(1)最简公分母是
(3)
把各分式化成相同
分母的分式叫做
分式的通分.
绝对值大于10的数记成a×10n的形式,其中1≤︱a︱<10,n是正整数.
例如:864000可以写成8.64×105.
科学记数法:
n等于原数的整数数位减1
我们可以利用10的负整数次幂,用科学记数法表示一些绝对值小于1的数,
即将它们表示成a×10-n的形式.
(其中n是正整数,1≤∣a∣<10.)
类似:
1. a0=1
规定
(其中n为正整数且
例1计算:
练习
1、若(2x-1)0=1,求x的取值范围。
2、下列计算正确的是( )
D
概括:分式方程
分母中含有未知数的方程,叫做分式方程
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
一化二解三检验
解分式方程的一般步骤
分式的基本性质:
分式的分子与分母同时乘以(或除以)同一个不等于零的整式 ,分式的值不变.
练习1. 填空:
.
三、例题讲解与练习
4n
a2+ab
x
不改变分式的值,把下列各式的分子与分母的各项系数都化为整数.
⑴ ⑵
(3)
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。
用符号语言表达:
两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘。
用符号语言表达:
例1 计算:
注意:乘法运算时,分子或分母能分解的要分解.
(1)分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
(2)分子相加减时,如果分子是一个多项式,要将分子看成一个整体,先用括号括起来,再运算,可减少出现符号错误。
(3)分式加减运算的结果要约分,化为最 简分式(或整式)。
练习:用科学记数法表示下列个数
0.000000108
-0.00003
3.
2.
1.
-56700000
4.
6.
-0.0000067
5.
复
习:
正整数指数幂的运算性质:
1)am·an=am+n (a≠0 m、n为正整数)
2)(am)n=amn (a≠0 m、n为正整数)
3)(ab)n=anbn(a,b≠0 m、n为正整数)
4)am÷an=am-n (a≠0 m、n为正整数且 m>n)
5) ( b≠0 ,n是正整数)
当a≠0时,a0=1。(0指数幂的运算)
6)
例1计算:
1、2(x-1)=x+1; x2+x-20=0; x+2y=1…
2、
整式方程:
方程两边都是整式的方程.
分式方程:
分母中含有未知数的方程.
观察下列方程:
概 念
一元一次方程
一元二次方程
解分式方程
化简,得整式方程 2(x-9)=x+9
解整式方程,得 x= 27.
当x=27时, 2(x+9) ≠0
∴ x = 27是原方程的解.
● ● ● ● ●
分式方程
整式方程
解整式方程
检 验
转化
① ② ③
检验:
解: 方程的两边同乘以最简公分母2(x+9),
得,
梳理
(1) 分式是两个整式相除的商,分数线可以理解为除号,并含有括号的作用.
(2) 分式的分子可以含有字母,也可以不含有字母,但分母必须含有字母.
有理式
整式
分式
如何判断一个式 子是否是分式?
2、下列代数式中,哪些是分式
; (2) ; (3) ;
(4) ; (5) ; (6) .
(1)x÷y ;
(2)6000÷ab ;
(3)a÷(b+c) ;
(4)(a-b)÷c ;
(5)(x-y)÷(x+y) ;
练习
1、把下列式子写成分式的形式。
√
√
√
探究
由于字母可以表示不同的数,所以分式比分数更具有一般性。例如,分数 仅表示2÷3的商,而分式 既可以表示2÷3,又可以表示-5÷2,8÷(-9)等。
分式中的分母应满足什么条件?
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义。
例题
当x为何值时,分式 有意义?
解:
要使分式 有意义,
必须
3x≠0
即x≠0
∴当x≠0时,分式 有意义。
例1
(1)当x 时,分式 有意义;
(2)当b 时,分式 有意义;
(3)当x,y满足关系 时,分式
有意义;
例2 填空:
解:
(1)当分母x-1≠0即x≠1时,分式 有
意义;
(2)当分母5-3b≠0即b≠ 时,分式
有意义;
(3)当分母x-y≠0即x≠y时,分式
有意义;
若把题目要求改为:“当 取何值时下列分式无意义?”如何解答?
当x取什么值时,下列分式有意义?
; (2) ;
(3) ; (4) .
练习
(2) 由分母 , 得 .
∴当 时,分式 有意义.
(3)∵x2+1≥0恒成立, .
∴ 取任何实数时,原分式都有意义.
(4) 由分母 ,得 .
∴当 时,原分式有意义.
解:(1) 由分母得 ,
∴当 时,分式 有意义.
分式 在什么条件下值为0?
分式的值为0,需满足的条件是:分子的值等于0且分母值不为0.
仅仅是 就可以了吗?
A=0
且B≠0
当x取什么值时,分式
的值为零?
所以,在x+2=0,并且2x-5≠0时,分式的值为零。
例题
分析:分式的值为0,需满足的条件是:分子的值等于0且分母值不为0.
解:
要使原分式的值为零,必须:
x+2=0, 且2x-5≠0
∴x=-2 , 且x ≠
∴当x=-2 时,原分式值为零。
因为x=-2时,分母2x-5≠0,
1、在下列各分式中,当 等于什么数时,分式的值为0?当 等于什么数时,分式没有意义?
(1) ; (2) .
2、分式 的值能等于0吗?说明理由.
练习
1、形如 且B中含有字母的式子叫做分式。其中B≠0。整式和分式统称为有理式。
(3)分式中,当A=0且B ≠ 0时,分式 的值为零。
2.(1)分式中B≠0时,分式 有意义;
(2)分式中B=0,分式 无意义;
小结
2.当 时,则分式 有意义.
3.若分式 的值等于零,则应满足的
条件是 .
1.在代数式
中,分式共有_____个。
3
x=2
x≠3且x ≠-3
巩固练习
1、当x=-2时,分式
没有
意义,求a。
2、当x=3时,分式
零,求a。
的值为
思考
