图形的旋转导学案
图片预览


文档简介
第23章 图形的旋转导学案
23.1图形的旋转 第1课时
学习目标:
1、了解旋转及其旋转中心和旋转角等相关概念
2、理解旋转的基本性质并利用性质解决相关问题。
重点:旋转及对应点的有关概念及其应用。
难点:从活生生的数学中抽象出概念。
学习过程
(一)学生预习 教师导学
观察下列图片:
(1) 时钟上的秒针在不停的转动; (2) 大风车的转动;
(3) 飞速转动的电风扇叶片; (4)荡秋千
(5) 由平面图形转动而产生的奇妙图案。 (6)汽车上的雨刮器
●这些情景中的转动现象,有什么共同特征
(二)学生探究 教师引领
建立旋转的概念
试一试,请同学们尝试用自己的语言来描述以下旋转.
(
抽象出点的旋转
A
B
(图1)
O
)
··○○○
问题:单摆上小球的转动由位置A转到B,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度
(
抽象出线的旋转
·
O
A
B
C
D
(图2)
)
(
抽象出三角形的旋转
·
O
A
B
C
F
D
E
(图3)
)
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B;
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD;
图3:在同一平面内,△ABC绕着定点O旋转某一角度得到△DEF。
旋转定义:像这样,把一个图形绕着某一点O_____________的图形变换叫做旋转.
点O叫做___________,转动的角叫做_________。
旋转的三个要素:____________、____________、_______________。
思考:
①同学们观察图3,点A,线段AB,∠ABC分别转到了什么位置?
②请找出图3中其他的对应点、对应线段、对应角,并指出旋转中心和旋转角度。
(三)学生展示 教师激励
(
C
A
B
O
D
) 如图,△ABO绕点O旋转得到△CDO,则:
点B的对应点是点_________________;
线段OB的对应线段是线段__________;
线段AB的对应线段是线段__________;
∠A的对应角是___________________;
∠B的对应角是___________________;
旋转中心是点____________________;
旋转角是 ___________ 与__________.
(2) 如图,香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中的一瓣经过几次旋转得到的 旋转角∠AOB多少度? 你知道∠COD等于多少度吗?
(
·
·
A
B
O
D
C
)
(四)学生归纳 教师提炼
1.从我们看到的旋转现象,你认为旋转的主要决定因素是什么?
2.在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
在图形的旋转过程中,图形上各个点旋转的角度有什么关系吗?
旋转的性质:
1、对应点到旋转中心的距离 ___________ ;
2、任意一对对应点与旋转中心所连线段的夹角都等于 ;
3、旋转前后的图形 _______________________ 。
(五)学生达标 教师测评
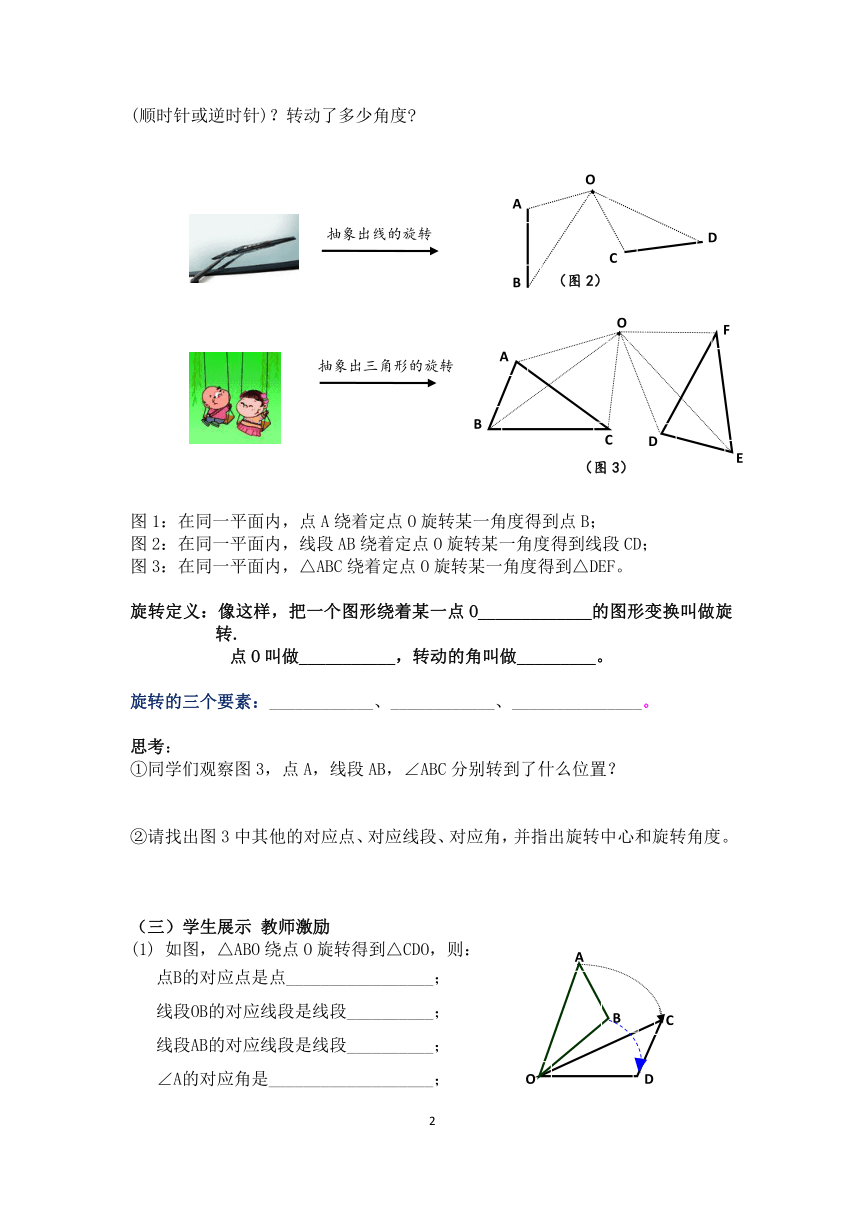
1.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.
在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
(
O
A
B
D
E
C
F
)
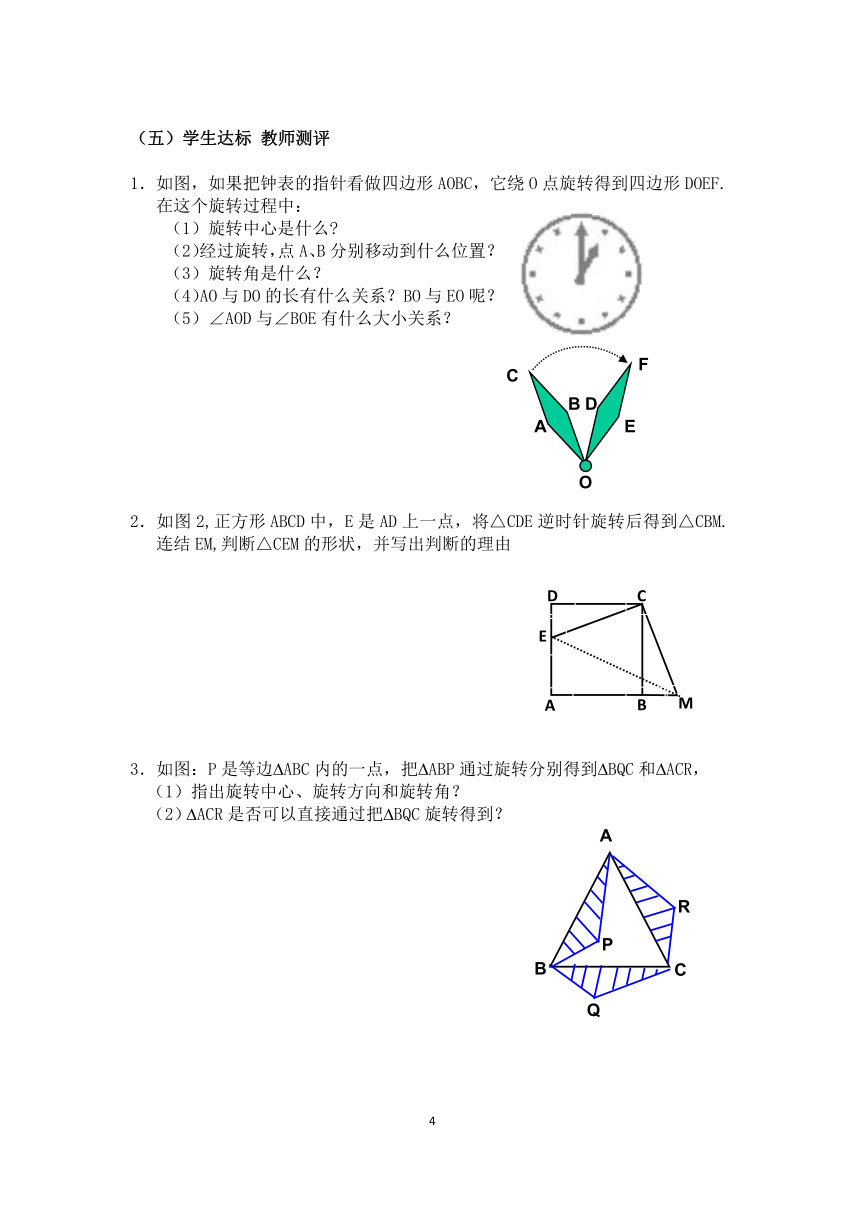
2.如图2,正方形ABCD中,E是AD上一点,将△CDE逆时针旋转后得到△CBM.连结EM,判断△CEM的形状,并写出判断的理由
(
C
A
B
D
E
M
)
3.如图:P是等边ABC内的一点,把ABP通过旋转分别得到BQC和ACR,
(1)指出旋转中心、旋转方向和旋转角?
(
A
R
P
B
Q
C
)(2)ACR是否可以直接通过把BQC旋转得到?
23.1图形的旋转 第2课时
一、学习目标:
1、能够按照要求做出简单的图形旋转后的图形。
2、继续利用旋转的性质解决相关问题。
二、学习过程:
(一)学生预习 教师导学
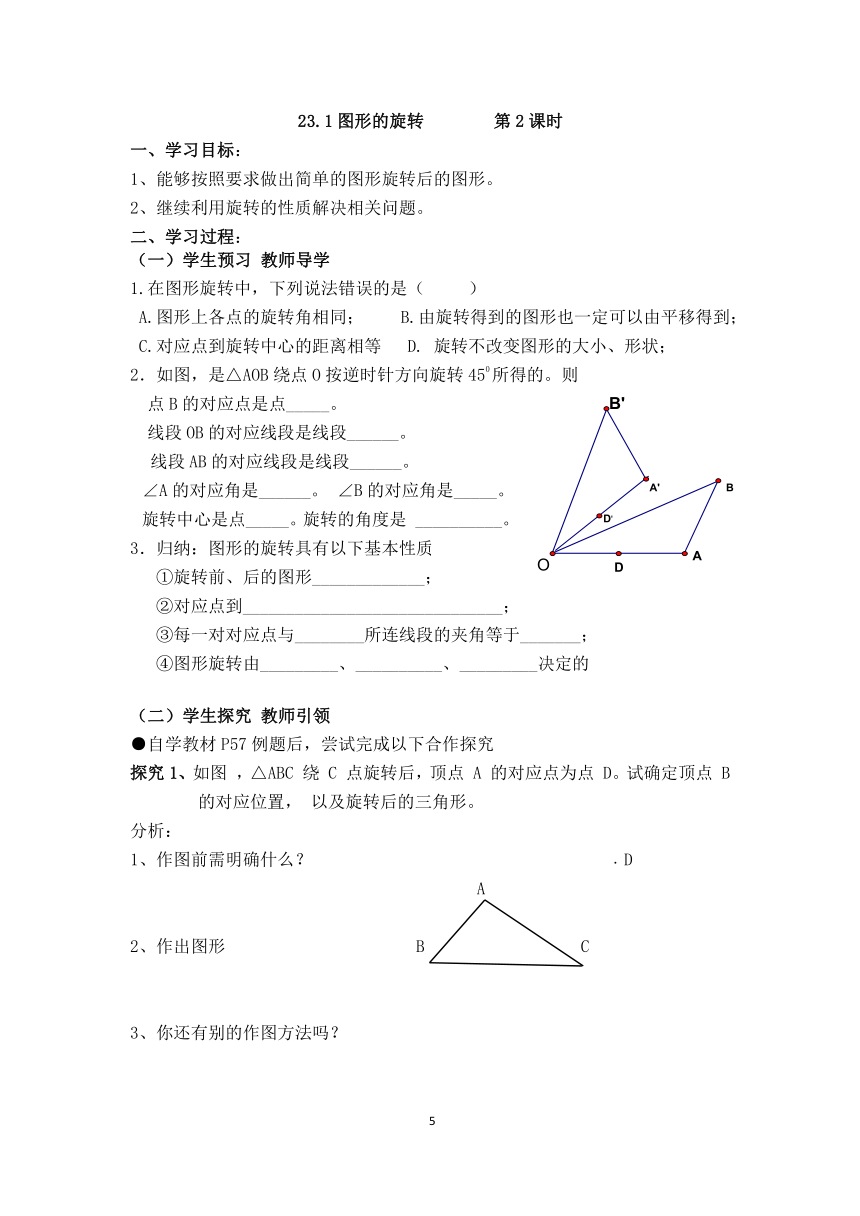
1.在图形旋转中,下列说法错误的是( )
A.图形上各点的旋转角相同; B.由旋转得到的图形也一定可以由平移得到;
C.对应点到旋转中心的距离相等 D. 旋转不改变图形的大小、形状;
2.如图,是△AOB绕点O按逆时针方向旋转450所得的。则
(
D
'
D
A'
A
B
O
B'
)点B的对应点是点_____。
线段OB的对应线段是线段______。
线段AB的对应线段是线段______。
∠A的对应角是______。 ∠B的对应角是_____。
旋转中心是点_____。旋转的角度是 __________。
3.归纳:图形的旋转具有以下基本性质
①旋转前、后的图形_____________;
②对应点到______________________________;
③每一对对应点与________所连线段的夹角等于_______;
④图形旋转由_________、__________、_________决定的
(二)学生探究 教师引领
●自学教材P57例题后,尝试完成以下合作探究
探究1、如图 ,△ABC 绕 C 点旋转后,顶点 A 的对应点为点 D。试确定顶点 B 的对应位置, 以及旋转后的三角形。
分析:
1、作图前需明确什么? ﹒D
A
2、作出图形 B C
3、你还有别的作图方法吗?
(三)学生展示 教师激励
练习:①在图1中画出△ABC绕点C顺时针旋转90°后的图形△A1B1C1
②在图2中画出△ABC绕点O逆时针旋转90°后的图形△A1B1C1
③图3中△A1B1C1是△ABC绕着某一点O旋转得到的图形,请在图中画出旋转中心O
(
A
)
(
B
) (
C
)
(
A
)
(
B
) (
C
)
(
O
) (
O
)
(
图2
) 图1
(
A
)
(
B
1
)
(
B
) (
C
) (
C
1
) (
A
1
)
图3
(四)学生归纳 教师提炼
旋转作图时需确定:__________________________________________
旋转中心在___________________________________________________
(五)学生达标 教师测评
当堂检测:
1.如果两个图形可通过旋转而相互得到,则下列说法中正确的有( ).
①对应点连线的中垂线必经过旋转中心. ②这两个图形大小、形状不变.
③将一个图形绕旋转中心旋转某个定角后必与另一个图形重合. ④对应线段一定相等且平行.
A.1个 B.2个 C.3个 D.4个
2.如图,菱形AEFG可以看成是把菱形ABCD以A为中心( ).
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
3. 如图所示,把一直角三角尺绕着300角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合。
(1)三角尺旋转了多少度?
(2)连接CD,试判断△CBD的形状。
(3)求∠BDC的度数。
4.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBP重合,若PB=3,求PP的长。
5. 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1,连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.
并以图2为例说明理由.
(
图1
)
(
图2
)
23.2.1中心对称
一、学习目标
1、掌握中心对称的定义以及相关概念。理解中心对称的性质,能够利用性质解决相关问题。
2、能够依据中心对称的性质解决相关作图问题。
二、重点:作图以及利用性质解决问题。 难点:利用性质解决问题。
三、学习过程:
(一)学生预习 教师导学
●自学教材P62回答下列问题。
1、自学教材P62并填空
把一个图形______________________________________________________那么就说这两个图形关于这个点中心对称。这个点叫_________________。
2、结合中心对称的定义回答:①中心对称揭示了_____个图形之间的对称关系。;②中心对称是把一个图形绕某一点作______°旋转与另一个图形重合。
(二)学生探究 教师引领
●自学教材P63探究并归纳:
1、中心对称的两个图形的对称点到__________的距离相等,即对称点的连线经过______________而且被______________平分。.
2、中心对称的两个图形是________________.
(三)学生展示 教师激励
●(可参看教材P64例1)
1、画出△ABC关于点O的中心对称图形。 2、△ABC与△DEF关于点O中心对称,作出对称中心。
A
﹒O
B
C
3.依据第2题的作图,回答:对称中心是_____,对应线段有_____________________________________. △ABC与△DEF是_________形,
点A、B、C的对称点分别为___________________.
(四)学生归纳 教师提炼
1、中心对称的定义:把一个图形绕着某一个点旋转1800,如果它能够与另一个图形重合,那么就称这两个图形关于这个点成中心对称(简称中心对称)
2、中心对称的性质:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分。
(五)学生达标 教师测评
●随堂检测:
1、关于中心对称的两个图形,对应线段的关系是( ).
(A)平行 (B)相等 (C)平行且相等 (D)相等且平行或在同一直线上
2、如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这两个图形一定关于这一点成____________对称.
3、ΔABC和ΔA’B’C’关于点O中心对称,若ΔABC的周长为12cm,ΔA’B’C’的面积为6cm2,则ΔA’B’C’的周长为________,ΔABC的面积为________。
4、已知点O是平行四边形 ABCD对角线的交点,则图中
关于点 O对称的三角形有_____对,它们分别是:___________________________________________
5、 在右面四个图形中,
图形①与________成轴对称,图形①与________成中心对称.
6、如图: 请你在下图的正方形格纸中,画出线段AB关于点O成中心对称的图形。
7、如图1,等腰梯形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下列关于点O成中心对称的一组三角形是( ).
A.△AOB与△COD B.△AOD与△BOC C.△CDO与△EFO D.△ADC与△BCD
●回顾本节课,谈谈收获与不足
23.2.2中心对称图形
一、学习目标:
正确认识什么是中心对称图形,能够判别一个图形是不是中心对称图形。
理解中心对称图形与中心对称的区别与联系。
二、重点:能够判别一个图形是不是中心对称图形。
难点:理解中心对称图形与中心对称的区别与联系。
三、学习过程:
(一)学生预习 教师导学
●自学教材P65,回答下列问题:
1、把一个图形________________________如果旋转后______________________那么这个图形就叫做中心对称图形。这个点叫___________。
2、明确定义内涵:①中心对称图形揭示了_____个图形本身的对称性质。;②中心对称图形是把一个图形绕某一点作______°旋转与原来图形重合。
3、由定义可知,线段、平行四边形______(填是或者不是)中心对称图形。
(二)学生探究 教师引领
●中心对称图形与中心对称的区别与联系。
区别:1、从图形个数上来说:_______________________________________
2、从定义上来说:中心对称图形揭示了具有___________性质的一种图形,而中心对称揭示了_____个图形之间的一种________关系。
联系:1、从旋转的角度说明:
2、从性质上说明:
●中心对称图形与轴对称图形的区别与联系:
(三)学生达标 教师测评
1、等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( ).
A.1个 B.2个 C.3个 D.4个
2、 下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3、下列图形中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形,是轴对称图形,但不是中心对称图形是________________
4、下图中,属于中心对称图形的有 .
A B C D
5、如图,在矩形ABCD中,对角线交于点O,过点O的直线交AD与BC于点E、F,AB=2,BC=3,则图中阴影部分的面积是________________.
6、已知点O是四边形ABCD的对称中心,
求证:四边形 ABCD是平行四边形。
(四)学生归纳 教师提炼
中心对称图形:是指一个图形绕着某一个点旋转1800后,能够与原来图形重合的图形。属于一个图形的对称性质
中 心 对 称:是指一个图形绕着某一个点旋转1800后,能够与另一图形重合。属于两个图形之间的对称关系
●总结本节课的收获与不足。
23.2.3关于原点对称的点的坐标
一、学习目标:掌握关于原点对称的点的坐标特征,能够运用特征解决相关问题。
二、学习过程:
(一)学生预习 教师导学
1、复习回顾
(1)点A(-2,1)关于x轴的对称点为A′( , );
(2)点B(2,-3)关于y轴的对称点为B′( , );
(3)点P(x,y)关于x轴的对称点为P′( , );
点P(x,y)关于y轴的对称点为P′( , );
2、思考:点P(x,y)关于原点的对称点的坐标有什么规律呢?
(二)学生探究 教师引领
1、自学课本p66完成探究
2、自学测试:
点A(3,2)关于原点的对称点为A′( , )
点B(-3,2)关于原点的对称点为B′( , ),
点C(3,0)关于原点的对称点为C′( , );
点P(x,y)关于原点的对称点为P′( , );
(三)学生归纳 教师提炼
●归纳:
两个点关于原点对称时,它们的坐标符号 ,即点P(x,y)关于原点的对称点P′(___________,___________)
(四)学生展示 教师激励
如图,利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形
(五)学生达标 教师测评
●当堂检测
1、点P(-3,-1)关于x轴对称的点P1的坐标是____关于y轴对称的点P2的坐标是________.关于原点对称的点的坐标为____________。
2、已知点A(m,1)与点B(3,n)关于原点对称,则m=_______,n=_______.
3、已知点A与B关于原点对称,则=__________.
4、点M(4,3)关于原点对称的点是点N,则线段MN=______________.
5、如图点A,B,C的坐标分别为 从下面四个点,,,中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.点M B.点N C.点P D.点Q
6.在平面直角坐标系中,点A的坐标为(1,4),将
线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是_________
7、矩形ABCD的对称中心经过原点,点B的坐标为(-2,-3),则点D的坐标为_____________.
8、点M(1-x,1-y)在第二象限,那么点N(1-x,y-1)关于原点对称的点的在第______象限。
拓展题:在平面直角坐标系中,已知3个点的坐标分别为、、. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以为对称中心的对称点,第2次电子蛙由点跳到以为对称中心的对称点,第3次电子蛙由点跳到以为对称中心的对称点,…,按此规律,电子蛙分别以、、为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是_________.
反思收获与不足:
图形的旋转复习
本章知识
旋转定义;旋转的性质;中心对称的性质;中心对称图形;图形变换。
测试题
A组
1. 在平面内,将一个图形绕一个 ___ 沿某个方向转动一个 ________ ,这样的图形运动称为旋转。这个 称为 _,转动的 ______称为 。
2. 旋转性质:(1)对应点到旋转中心的 相等; (2)任意一对对应点与旋转中心所连的 都是旋转角; (3)图形上的每一个点都绕旋转中心沿相同方向转动了 的角度.即旋转角 ______ 。
3. 在平面内,一个图形绕某个点旋转 _,如果旋转前后的图形互相 ____ ,那么这两个图形叫做中心对称,这个点叫做它的 。
中心对称图形上的每一对对应点所连成的线段都被对称中心 _________ 。
点P(x,y)关于原点对称的点是________,关于x轴对称的点是________,关于y轴对称的点是____________.
6. 中心对称与中心对称图形两个概念的区别和联系:
中心对称是 全等图形之间的 ; 中心对称图形是 图形本身成对称的 。
中心对称的两个图形性质:成中心对称的两个图形是 ;成中心对称的两个图形,对称点的连线都经过 ,并且被对称中心 。
7.下列图形中,是中心对称图形又是轴对称图形的有
______________________________________________
平行四边形; (2)菱形; (3)矩形; (4)正方形; (5)等腰梯形;
(6)等边三角形; (7)线段; (8)线段; (9)圆; (10)角;
8.如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点
(2)旋转角是多少度
(3)∠EAF等于多少度
(4)经过旋转,点B与点E分别移动到什么位置
(5)若点G是线段BE的中点,经过旋转后,点G移到了什么位置 在图形上作出.
E
G
(6)连结EF,请判断△AEF的形状,并说明理由. A B
(7)试判断四边形ABCD与AFCE面积的大小关系
D H F C
9、一个平行四边形绕着它对角线的交点旋转90○能够与它本身重合,则该四边形( )
A.矩形 B.菱形 C.正方形 D.无法确定
10、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A. ΔABC和ΔADE B. ΔABC和ΔABD
C. ΔABD和ΔACE D. ΔACE和ΔADE
11、钟表的秒针匀速旋转一周需要60秒.20秒内,秒针旋转的角度是 ;分针经过15 分后,分针转过的角度是 ;分针从数字12出发,转过150○,则它指的数字是 ;
12、如图,中,,.
(1)将向右平移个单位长度,
画出平移后的;
(2)画出关于轴对称的;
(3)将绕原点旋转,
画出旋转后的;
(4)在,,中,____与_____成轴对称,对称轴是_____;_____与_____成中心对称,对称中心的坐标是______。
13、如图,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,
△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
14、如图,△ABC绕着点C顺时针旋转35°得到△C ,若⊥AC,则
∠A的度数是 。
15、 如图,△ABC绕点B逆时针方向旋转到△EBF的位置 ,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC= ,旋转角是 。
16、如图,等腰△ABC绕点A旋转到△ACD的位置。已知∠ABC=80°,则在这个图中,点B的对应点是 ,BC= ,∠ACD= ,旋转中心是 ,旋转角是 。
反思:
7
23.1图形的旋转 第1课时
学习目标:
1、了解旋转及其旋转中心和旋转角等相关概念
2、理解旋转的基本性质并利用性质解决相关问题。
重点:旋转及对应点的有关概念及其应用。
难点:从活生生的数学中抽象出概念。
学习过程
(一)学生预习 教师导学
观察下列图片:
(1) 时钟上的秒针在不停的转动; (2) 大风车的转动;
(3) 飞速转动的电风扇叶片; (4)荡秋千
(5) 由平面图形转动而产生的奇妙图案。 (6)汽车上的雨刮器
●这些情景中的转动现象,有什么共同特征
(二)学生探究 教师引领
建立旋转的概念
试一试,请同学们尝试用自己的语言来描述以下旋转.
(
抽象出点的旋转
A
B
(图1)
O
)
··○○○
问题:单摆上小球的转动由位置A转到B,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度
(
抽象出线的旋转
·
O
A
B
C
D
(图2)
)
(
抽象出三角形的旋转
·
O
A
B
C
F
D
E
(图3)
)
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B;
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD;
图3:在同一平面内,△ABC绕着定点O旋转某一角度得到△DEF。
旋转定义:像这样,把一个图形绕着某一点O_____________的图形变换叫做旋转.
点O叫做___________,转动的角叫做_________。
旋转的三个要素:____________、____________、_______________。
思考:
①同学们观察图3,点A,线段AB,∠ABC分别转到了什么位置?
②请找出图3中其他的对应点、对应线段、对应角,并指出旋转中心和旋转角度。
(三)学生展示 教师激励
(
C
A
B
O
D
) 如图,△ABO绕点O旋转得到△CDO,则:
点B的对应点是点_________________;
线段OB的对应线段是线段__________;
线段AB的对应线段是线段__________;
∠A的对应角是___________________;
∠B的对应角是___________________;
旋转中心是点____________________;
旋转角是 ___________ 与__________.
(2) 如图,香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中的一瓣经过几次旋转得到的 旋转角∠AOB多少度? 你知道∠COD等于多少度吗?
(
·
·
A
B
O
D
C
)
(四)学生归纳 教师提炼
1.从我们看到的旋转现象,你认为旋转的主要决定因素是什么?
2.在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
在图形的旋转过程中,图形上各个点旋转的角度有什么关系吗?
旋转的性质:
1、对应点到旋转中心的距离 ___________ ;
2、任意一对对应点与旋转中心所连线段的夹角都等于 ;
3、旋转前后的图形 _______________________ 。
(五)学生达标 教师测评
1.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.
在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
(
O
A
B
D
E
C
F
)
2.如图2,正方形ABCD中,E是AD上一点,将△CDE逆时针旋转后得到△CBM.连结EM,判断△CEM的形状,并写出判断的理由
(
C
A
B
D
E
M
)
3.如图:P是等边ABC内的一点,把ABP通过旋转分别得到BQC和ACR,
(1)指出旋转中心、旋转方向和旋转角?
(
A
R
P
B
Q
C
)(2)ACR是否可以直接通过把BQC旋转得到?
23.1图形的旋转 第2课时
一、学习目标:
1、能够按照要求做出简单的图形旋转后的图形。
2、继续利用旋转的性质解决相关问题。
二、学习过程:
(一)学生预习 教师导学
1.在图形旋转中,下列说法错误的是( )
A.图形上各点的旋转角相同; B.由旋转得到的图形也一定可以由平移得到;
C.对应点到旋转中心的距离相等 D. 旋转不改变图形的大小、形状;
2.如图,是△AOB绕点O按逆时针方向旋转450所得的。则
(
D
'
D
A'
A
B
O
B'
)点B的对应点是点_____。
线段OB的对应线段是线段______。
线段AB的对应线段是线段______。
∠A的对应角是______。 ∠B的对应角是_____。
旋转中心是点_____。旋转的角度是 __________。
3.归纳:图形的旋转具有以下基本性质
①旋转前、后的图形_____________;
②对应点到______________________________;
③每一对对应点与________所连线段的夹角等于_______;
④图形旋转由_________、__________、_________决定的
(二)学生探究 教师引领
●自学教材P57例题后,尝试完成以下合作探究
探究1、如图 ,△ABC 绕 C 点旋转后,顶点 A 的对应点为点 D。试确定顶点 B 的对应位置, 以及旋转后的三角形。
分析:
1、作图前需明确什么? ﹒D
A
2、作出图形 B C
3、你还有别的作图方法吗?
(三)学生展示 教师激励
练习:①在图1中画出△ABC绕点C顺时针旋转90°后的图形△A1B1C1
②在图2中画出△ABC绕点O逆时针旋转90°后的图形△A1B1C1
③图3中△A1B1C1是△ABC绕着某一点O旋转得到的图形,请在图中画出旋转中心O
(
A
)
(
B
) (
C
)
(
A
)
(
B
) (
C
)
(
O
) (
O
)
(
图2
) 图1
(
A
)
(
B
1
)
(
B
) (
C
) (
C
1
) (
A
1
)
图3
(四)学生归纳 教师提炼
旋转作图时需确定:__________________________________________
旋转中心在___________________________________________________
(五)学生达标 教师测评
当堂检测:
1.如果两个图形可通过旋转而相互得到,则下列说法中正确的有( ).
①对应点连线的中垂线必经过旋转中心. ②这两个图形大小、形状不变.
③将一个图形绕旋转中心旋转某个定角后必与另一个图形重合. ④对应线段一定相等且平行.
A.1个 B.2个 C.3个 D.4个
2.如图,菱形AEFG可以看成是把菱形ABCD以A为中心( ).
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
3. 如图所示,把一直角三角尺绕着300角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合。
(1)三角尺旋转了多少度?
(2)连接CD,试判断△CBD的形状。
(3)求∠BDC的度数。
4.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBP重合,若PB=3,求PP的长。
5. 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1,连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.
并以图2为例说明理由.
(
图1
)
(
图2
)
23.2.1中心对称
一、学习目标
1、掌握中心对称的定义以及相关概念。理解中心对称的性质,能够利用性质解决相关问题。
2、能够依据中心对称的性质解决相关作图问题。
二、重点:作图以及利用性质解决问题。 难点:利用性质解决问题。
三、学习过程:
(一)学生预习 教师导学
●自学教材P62回答下列问题。
1、自学教材P62并填空
把一个图形______________________________________________________那么就说这两个图形关于这个点中心对称。这个点叫_________________。
2、结合中心对称的定义回答:①中心对称揭示了_____个图形之间的对称关系。;②中心对称是把一个图形绕某一点作______°旋转与另一个图形重合。
(二)学生探究 教师引领
●自学教材P63探究并归纳:
1、中心对称的两个图形的对称点到__________的距离相等,即对称点的连线经过______________而且被______________平分。.
2、中心对称的两个图形是________________.
(三)学生展示 教师激励
●(可参看教材P64例1)
1、画出△ABC关于点O的中心对称图形。 2、△ABC与△DEF关于点O中心对称,作出对称中心。
A
﹒O
B
C
3.依据第2题的作图,回答:对称中心是_____,对应线段有_____________________________________. △ABC与△DEF是_________形,
点A、B、C的对称点分别为___________________.
(四)学生归纳 教师提炼
1、中心对称的定义:把一个图形绕着某一个点旋转1800,如果它能够与另一个图形重合,那么就称这两个图形关于这个点成中心对称(简称中心对称)
2、中心对称的性质:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分。
(五)学生达标 教师测评
●随堂检测:
1、关于中心对称的两个图形,对应线段的关系是( ).
(A)平行 (B)相等 (C)平行且相等 (D)相等且平行或在同一直线上
2、如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这两个图形一定关于这一点成____________对称.
3、ΔABC和ΔA’B’C’关于点O中心对称,若ΔABC的周长为12cm,ΔA’B’C’的面积为6cm2,则ΔA’B’C’的周长为________,ΔABC的面积为________。
4、已知点O是平行四边形 ABCD对角线的交点,则图中
关于点 O对称的三角形有_____对,它们分别是:___________________________________________
5、 在右面四个图形中,
图形①与________成轴对称,图形①与________成中心对称.
6、如图: 请你在下图的正方形格纸中,画出线段AB关于点O成中心对称的图形。
7、如图1,等腰梯形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下列关于点O成中心对称的一组三角形是( ).
A.△AOB与△COD B.△AOD与△BOC C.△CDO与△EFO D.△ADC与△BCD
●回顾本节课,谈谈收获与不足
23.2.2中心对称图形
一、学习目标:
正确认识什么是中心对称图形,能够判别一个图形是不是中心对称图形。
理解中心对称图形与中心对称的区别与联系。
二、重点:能够判别一个图形是不是中心对称图形。
难点:理解中心对称图形与中心对称的区别与联系。
三、学习过程:
(一)学生预习 教师导学
●自学教材P65,回答下列问题:
1、把一个图形________________________如果旋转后______________________那么这个图形就叫做中心对称图形。这个点叫___________。
2、明确定义内涵:①中心对称图形揭示了_____个图形本身的对称性质。;②中心对称图形是把一个图形绕某一点作______°旋转与原来图形重合。
3、由定义可知,线段、平行四边形______(填是或者不是)中心对称图形。
(二)学生探究 教师引领
●中心对称图形与中心对称的区别与联系。
区别:1、从图形个数上来说:_______________________________________
2、从定义上来说:中心对称图形揭示了具有___________性质的一种图形,而中心对称揭示了_____个图形之间的一种________关系。
联系:1、从旋转的角度说明:
2、从性质上说明:
●中心对称图形与轴对称图形的区别与联系:
(三)学生达标 教师测评
1、等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( ).
A.1个 B.2个 C.3个 D.4个
2、 下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3、下列图形中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形,是轴对称图形,但不是中心对称图形是________________
4、下图中,属于中心对称图形的有 .
A B C D
5、如图,在矩形ABCD中,对角线交于点O,过点O的直线交AD与BC于点E、F,AB=2,BC=3,则图中阴影部分的面积是________________.
6、已知点O是四边形ABCD的对称中心,
求证:四边形 ABCD是平行四边形。
(四)学生归纳 教师提炼
中心对称图形:是指一个图形绕着某一个点旋转1800后,能够与原来图形重合的图形。属于一个图形的对称性质
中 心 对 称:是指一个图形绕着某一个点旋转1800后,能够与另一图形重合。属于两个图形之间的对称关系
●总结本节课的收获与不足。
23.2.3关于原点对称的点的坐标
一、学习目标:掌握关于原点对称的点的坐标特征,能够运用特征解决相关问题。
二、学习过程:
(一)学生预习 教师导学
1、复习回顾
(1)点A(-2,1)关于x轴的对称点为A′( , );
(2)点B(2,-3)关于y轴的对称点为B′( , );
(3)点P(x,y)关于x轴的对称点为P′( , );
点P(x,y)关于y轴的对称点为P′( , );
2、思考:点P(x,y)关于原点的对称点的坐标有什么规律呢?
(二)学生探究 教师引领
1、自学课本p66完成探究
2、自学测试:
点A(3,2)关于原点的对称点为A′( , )
点B(-3,2)关于原点的对称点为B′( , ),
点C(3,0)关于原点的对称点为C′( , );
点P(x,y)关于原点的对称点为P′( , );
(三)学生归纳 教师提炼
●归纳:
两个点关于原点对称时,它们的坐标符号 ,即点P(x,y)关于原点的对称点P′(___________,___________)
(四)学生展示 教师激励
如图,利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形
(五)学生达标 教师测评
●当堂检测
1、点P(-3,-1)关于x轴对称的点P1的坐标是____关于y轴对称的点P2的坐标是________.关于原点对称的点的坐标为____________。
2、已知点A(m,1)与点B(3,n)关于原点对称,则m=_______,n=_______.
3、已知点A与B关于原点对称,则=__________.
4、点M(4,3)关于原点对称的点是点N,则线段MN=______________.
5、如图点A,B,C的坐标分别为 从下面四个点,,,中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.点M B.点N C.点P D.点Q
6.在平面直角坐标系中,点A的坐标为(1,4),将
线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是_________
7、矩形ABCD的对称中心经过原点,点B的坐标为(-2,-3),则点D的坐标为_____________.
8、点M(1-x,1-y)在第二象限,那么点N(1-x,y-1)关于原点对称的点的在第______象限。
拓展题:在平面直角坐标系中,已知3个点的坐标分别为、、. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以为对称中心的对称点,第2次电子蛙由点跳到以为对称中心的对称点,第3次电子蛙由点跳到以为对称中心的对称点,…,按此规律,电子蛙分别以、、为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是_________.
反思收获与不足:
图形的旋转复习
本章知识
旋转定义;旋转的性质;中心对称的性质;中心对称图形;图形变换。
测试题
A组
1. 在平面内,将一个图形绕一个 ___ 沿某个方向转动一个 ________ ,这样的图形运动称为旋转。这个 称为 _,转动的 ______称为 。
2. 旋转性质:(1)对应点到旋转中心的 相等; (2)任意一对对应点与旋转中心所连的 都是旋转角; (3)图形上的每一个点都绕旋转中心沿相同方向转动了 的角度.即旋转角 ______ 。
3. 在平面内,一个图形绕某个点旋转 _,如果旋转前后的图形互相 ____ ,那么这两个图形叫做中心对称,这个点叫做它的 。
中心对称图形上的每一对对应点所连成的线段都被对称中心 _________ 。
点P(x,y)关于原点对称的点是________,关于x轴对称的点是________,关于y轴对称的点是____________.
6. 中心对称与中心对称图形两个概念的区别和联系:
中心对称是 全等图形之间的 ; 中心对称图形是 图形本身成对称的 。
中心对称的两个图形性质:成中心对称的两个图形是 ;成中心对称的两个图形,对称点的连线都经过 ,并且被对称中心 。
7.下列图形中,是中心对称图形又是轴对称图形的有
______________________________________________
平行四边形; (2)菱形; (3)矩形; (4)正方形; (5)等腰梯形;
(6)等边三角形; (7)线段; (8)线段; (9)圆; (10)角;
8.如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点
(2)旋转角是多少度
(3)∠EAF等于多少度
(4)经过旋转,点B与点E分别移动到什么位置
(5)若点G是线段BE的中点,经过旋转后,点G移到了什么位置 在图形上作出.
E
G
(6)连结EF,请判断△AEF的形状,并说明理由. A B
(7)试判断四边形ABCD与AFCE面积的大小关系
D H F C
9、一个平行四边形绕着它对角线的交点旋转90○能够与它本身重合,则该四边形( )
A.矩形 B.菱形 C.正方形 D.无法确定
10、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A. ΔABC和ΔADE B. ΔABC和ΔABD
C. ΔABD和ΔACE D. ΔACE和ΔADE
11、钟表的秒针匀速旋转一周需要60秒.20秒内,秒针旋转的角度是 ;分针经过15 分后,分针转过的角度是 ;分针从数字12出发,转过150○,则它指的数字是 ;
12、如图,中,,.
(1)将向右平移个单位长度,
画出平移后的;
(2)画出关于轴对称的;
(3)将绕原点旋转,
画出旋转后的;
(4)在,,中,____与_____成轴对称,对称轴是_____;_____与_____成中心对称,对称中心的坐标是______。
13、如图,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,
△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
14、如图,△ABC绕着点C顺时针旋转35°得到△C ,若⊥AC,则
∠A的度数是 。
15、 如图,△ABC绕点B逆时针方向旋转到△EBF的位置 ,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC= ,旋转角是 。
16、如图,等腰△ABC绕点A旋转到△ACD的位置。已知∠ABC=80°,则在这个图中,点B的对应点是 ,BC= ,∠ACD= ,旋转中心是 ,旋转角是 。
反思:
7
同课章节目录
