河北省衡水市武强高中校2022届高三上学期第一次月考数学试题(B卷)(Word版含答案)
文档属性
| 名称 | 河北省衡水市武强高中校2022届高三上学期第一次月考数学试题(B卷)(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 336.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览




文档简介
武强中学2021-2022学年度上学期第一次月考
高三年级数学试题(B)
一、单项选择题(本大题共8个小题,每小题5分,共40分)
1.若α是第四象限角,则π-α是第( )象限角.
A.一 B.二 C.三 D.四
2.复数,则( )
A. B.1 C. D.5
3.已知△ABC中,则△ABC是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
4.为了得到函数的图象.只需把函数的图象上所有的点( )
A.向左平行移动个单位长度B.向右平行移动个单位长度
C.向左平行移动个单位长度D.向右平行移动个单位长度
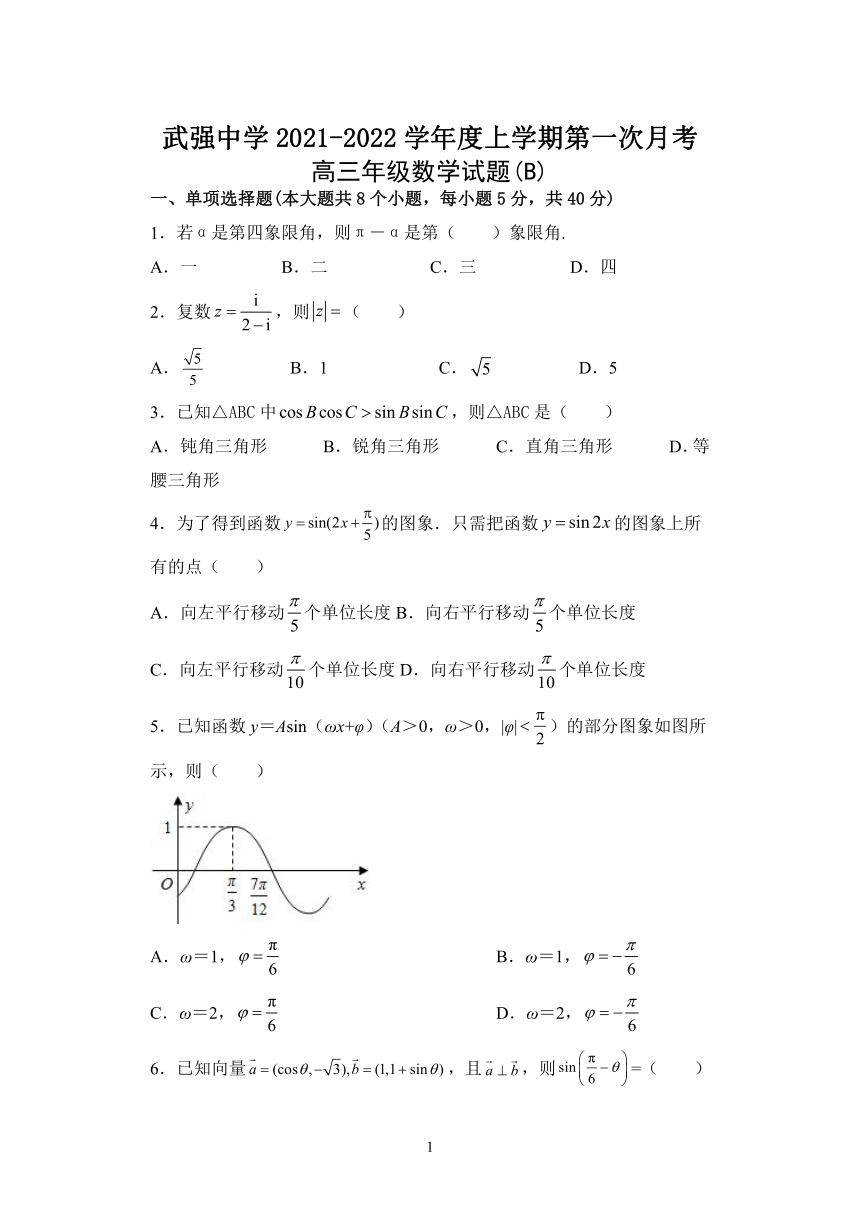
5.已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|)的部分图象如图所示,则( )
A.ω=1, B.ω=1,
C.ω=2, D.ω=2,
6.已知向量,且,则=( )
A. B. C. D.
7.已知向量,,,则的值是( )
A. B. C. D.
8.△ABC中,已知下列条件: ①; ②;③;④.其中满足上述条件的三角形有两解的是( )
A.①④ B.①② C.①②③ D.③④
二、多项选择题(本题共4个小题,每小题5分,共20分。在每个小题的选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分)
9.给出下列各三角函数值:①;②;③;④.其中符号为负的是( )
A.① B.② C.③ D.④
10.与向量(3,4)共线的单位向量( )
A. B. C. D.
11.已知复数(其中为虚数单位),下列说法正确的是( )
A. B.为实数
C.若,则复数z在复平面上对应的点落在第一象限
D.若,复数z是纯虚数,则
12.对于△ABC,有如下判断,其中正确的判断是( )
A.若,则△ABC为等腰三角形
B.在锐角△ABC中,一定有
C.若,,,则符合条件的△ABC有两个
D.若,则△ABC是锐角三角形
二、填空题(本大题共4个小题,每小题5分,共20分。)
13.已知非零向量,满足,且,则与的夹角为___________.
14..已知,则___________.
15.已知的三边分别为且,则的外接圆的周长为.
16.若复数为虚数单位为纯虚数,则的值为___________.
三.解答题:(本大题共6个小题,共70分。)
17.已知,,且.
(1)求x的值;
(2)求.
18.已知函数.
(1)求函数的最小正周期;
(2)求在区间上的单调递增区间.
19.在①,②,③这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求和的值;若问题中的三角形不存在,说明理由.
问题:是否存在△ABC,它的内角,,的对边分别为,,,且,,______?
注:如果选择多个条件分别解答,按第一个解答计分.
20.在中,已知角,,所对的边分别为,,,且,.
(1)求角的大小;
(2)若,求的长.
21.在△ABC中,是边的中线,,且.
(1)求△ABC的面积;
(2)若,求的长.
22.已知△ABC的内A、B、C所对的边分别是、、,若
(1)求角的值;
(2)求△ABC的面积取得最大值时,边的长.
高三数学(B)答案
CAACDBDB 9.ABC 10.BD 11.ABD 12.BC
13. 14. 15. 16.
17.(1),,即.
(2)由(1)知,则,.
18. (1)
,
的最小正周期为.
(2)由(1)
令
所以的单调递增区间为:
当时的单调递增区间为: 当时的单调递增区间为:
所以在区间上的单调递增区间为:
19.选择条件①:.由条件可得,,
由余弦定理得,即,
化简得,解得(舍去),从而.
选择条件②:.因为,
所以,再根据正弦定理有,
所以,由余弦定理得,即,所以.
选择条件③:.根据正弦定理可得,根据三角形的性质可知,即,即.
由得,显然不成立.所以不存在.
20.解析:(1)因为,,,
所以,
又,所以.
因为,且,又,所以,
同理可得,. 由正弦定理,得.
21.(1),则,
;
(2)由得,延长到,使,连接.
由平面向量加法的平行四边形法则可得,
所以,,,即的长为.
22.(1)由正弦定理可化为,即,
由余弦定理可得,因为,所以;
(2)因为,即,
所以,
当且仅当时,取最大值为,即有,解得.
(
- 1 -
)
高三年级数学试题(B)
一、单项选择题(本大题共8个小题,每小题5分,共40分)
1.若α是第四象限角,则π-α是第( )象限角.
A.一 B.二 C.三 D.四
2.复数,则( )
A. B.1 C. D.5
3.已知△ABC中,则△ABC是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
4.为了得到函数的图象.只需把函数的图象上所有的点( )
A.向左平行移动个单位长度B.向右平行移动个单位长度
C.向左平行移动个单位长度D.向右平行移动个单位长度
5.已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|)的部分图象如图所示,则( )
A.ω=1, B.ω=1,
C.ω=2, D.ω=2,
6.已知向量,且,则=( )
A. B. C. D.
7.已知向量,,,则的值是( )
A. B. C. D.
8.△ABC中,已知下列条件: ①; ②;③;④.其中满足上述条件的三角形有两解的是( )
A.①④ B.①② C.①②③ D.③④
二、多项选择题(本题共4个小题,每小题5分,共20分。在每个小题的选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分)
9.给出下列各三角函数值:①;②;③;④.其中符号为负的是( )
A.① B.② C.③ D.④
10.与向量(3,4)共线的单位向量( )
A. B. C. D.
11.已知复数(其中为虚数单位),下列说法正确的是( )
A. B.为实数
C.若,则复数z在复平面上对应的点落在第一象限
D.若,复数z是纯虚数,则
12.对于△ABC,有如下判断,其中正确的判断是( )
A.若,则△ABC为等腰三角形
B.在锐角△ABC中,一定有
C.若,,,则符合条件的△ABC有两个
D.若,则△ABC是锐角三角形
二、填空题(本大题共4个小题,每小题5分,共20分。)
13.已知非零向量,满足,且,则与的夹角为___________.
14..已知,则___________.
15.已知的三边分别为且,则的外接圆的周长为.
16.若复数为虚数单位为纯虚数,则的值为___________.
三.解答题:(本大题共6个小题,共70分。)
17.已知,,且.
(1)求x的值;
(2)求.
18.已知函数.
(1)求函数的最小正周期;
(2)求在区间上的单调递增区间.
19.在①,②,③这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求和的值;若问题中的三角形不存在,说明理由.
问题:是否存在△ABC,它的内角,,的对边分别为,,,且,,______?
注:如果选择多个条件分别解答,按第一个解答计分.
20.在中,已知角,,所对的边分别为,,,且,.
(1)求角的大小;
(2)若,求的长.
21.在△ABC中,是边的中线,,且.
(1)求△ABC的面积;
(2)若,求的长.
22.已知△ABC的内A、B、C所对的边分别是、、,若
(1)求角的值;
(2)求△ABC的面积取得最大值时,边的长.
高三数学(B)答案
CAACDBDB 9.ABC 10.BD 11.ABD 12.BC
13. 14. 15. 16.
17.(1),,即.
(2)由(1)知,则,.
18. (1)
,
的最小正周期为.
(2)由(1)
令
所以的单调递增区间为:
当时的单调递增区间为: 当时的单调递增区间为:
所以在区间上的单调递增区间为:
19.选择条件①:.由条件可得,,
由余弦定理得,即,
化简得,解得(舍去),从而.
选择条件②:.因为,
所以,再根据正弦定理有,
所以,由余弦定理得,即,所以.
选择条件③:.根据正弦定理可得,根据三角形的性质可知,即,即.
由得,显然不成立.所以不存在.
20.解析:(1)因为,,,
所以,
又,所以.
因为,且,又,所以,
同理可得,. 由正弦定理,得.
21.(1),则,
;
(2)由得,延长到,使,连接.
由平面向量加法的平行四边形法则可得,
所以,,,即的长为.
22.(1)由正弦定理可化为,即,
由余弦定理可得,因为,所以;
(2)因为,即,
所以,
当且仅当时,取最大值为,即有,解得.
(
- 1 -
)
同课章节目录
