2021年上海市闵行区重点中学高二月考数学试卷(2021.10) (图片版 含答案)
文档属性
| 名称 | 2021年上海市闵行区重点中学高二月考数学试卷(2021.10) (图片版 含答案) |

|
|
| 格式 | |||
| 文件大小 | 878.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 10:02:38 | ||
图片预览


文档简介
2021年上海市闵行中学高二月考数学试卷
021.10
填空题(共14题,每題3分,满分42分)
空间中三个平面最多可以将空间分为
部分
2.一个正四棱柱的底面边长为2,高为4,则该正四棱柱的体积为
3.将边长分别为lcm和2cm的矩形,绕边长为2cm的一边所在的直线旋转一周得到一圆
柱,则该圆柱的侧面积为
的所有棱长均为a,且其体积为163,则a
5.如图,已知长方体ABCD-ABCD的棱长A4=3cm,AB=4cm,AD=4cm
则点A到棱BC1的距离是
6.已知二面角a-l-B的大小为140°,直线a、b分别在平面a、β内,且都垂直于棱l
则a与b所成角的大小为
如图,在长方体ABCD-ABCD中,AB=1,AD=2,AA=2,则二面角
A-DD-B的平面角大小是6,则tan
8若两直线a、b与平面a所成的角相等,则a与b的位置关系是
9.已知正六棱柱的底面边长为2,侧棱为√3,则该正六棱柱的体积为
10.如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,则异面直线AP
与BD所成角的大小为
1l.如图,在体积为9的斜三棱柱ABC-ABC中,S是CC1上的一点,S-ABC的体积为
2,则三棱锥S-ABC的体积为
12.两个圆锥有等长的母线,它们的侧面展开图恰好拼成一个圆,若它们的侧面积之比为
1:2,则它们的体积比为
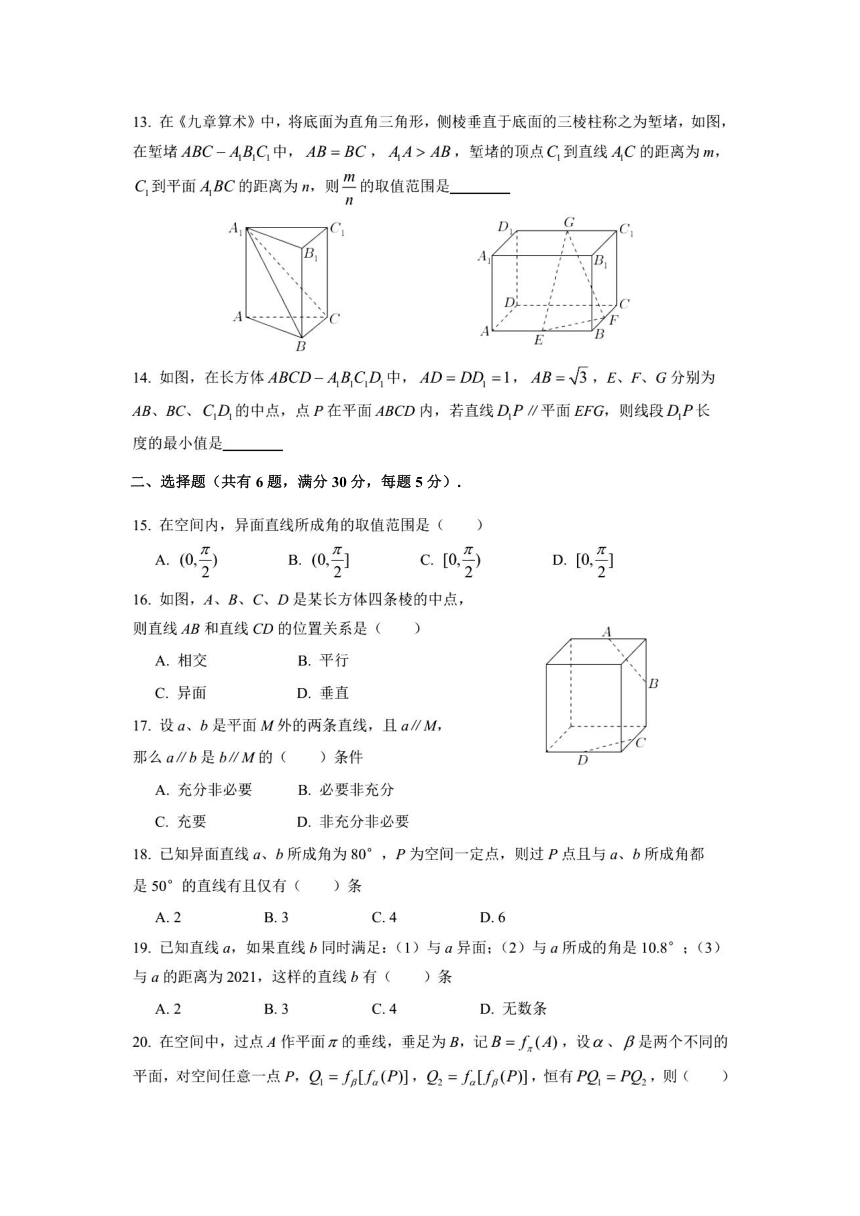
13.在《九章算术》中,将底面为直角三角形,侧棱垂直于底面的三棱柱称之为堑堵,如图
在堑堵ABC-ABC1中,AB=BC,AA>AB,堑堵的顶点C1到直线AC的距离为
C到平面A1BC的距离为n,则一的取值范围是
B
14.如图,在长方体ABCD-ABCD中,AD=D=1,AB=√3,E、F、G分别为
AB、BC、C1D的中点,点P在平面ABCD内,若直线DP∥平面EFG,则线段DP长
度的最小值是
选择题(共有6题,满分30分,每题5分
15.在空间内,异面直线所成角的取值范围是()
B.(0,
C.[0,-)
D.[0,-]
D是某长方体四条棱的中点,
则直线AB和直线CD的位置关系是()
A.相交
B.平行
异面
D.垂直
17.设a、b是平面M外的两条直线,且a∥M,
那么a∥b是b∥M的
条件
A.充分非必要
B.必要非充分
C.充要
D.非充分非必要
18.已知异面直线a、b所成角为80°,P为空间一定点,则过P点且与a、b所成角都
是50°的直线有且仅有()条
B.3
D.6
19.已知直线a,如果直线b同时满足:(1)与a异面;(2)与a所成的角是108°;(3)
与a的距离为2021,这样的直线b有()条
B
20.在空间中,过点A作平面z的垂线,垂足为B,记B=f(A),设a、B是两个不同的
平面,对空间任意一点P,Q=ff(P,Q2=fL(P,恒有PQ=PQ2,则()
021.10
填空题(共14题,每題3分,满分42分)
空间中三个平面最多可以将空间分为
部分
2.一个正四棱柱的底面边长为2,高为4,则该正四棱柱的体积为
3.将边长分别为lcm和2cm的矩形,绕边长为2cm的一边所在的直线旋转一周得到一圆
柱,则该圆柱的侧面积为
的所有棱长均为a,且其体积为163,则a
5.如图,已知长方体ABCD-ABCD的棱长A4=3cm,AB=4cm,AD=4cm
则点A到棱BC1的距离是
6.已知二面角a-l-B的大小为140°,直线a、b分别在平面a、β内,且都垂直于棱l
则a与b所成角的大小为
如图,在长方体ABCD-ABCD中,AB=1,AD=2,AA=2,则二面角
A-DD-B的平面角大小是6,则tan
8若两直线a、b与平面a所成的角相等,则a与b的位置关系是
9.已知正六棱柱的底面边长为2,侧棱为√3,则该正六棱柱的体积为
10.如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,则异面直线AP
与BD所成角的大小为
1l.如图,在体积为9的斜三棱柱ABC-ABC中,S是CC1上的一点,S-ABC的体积为
2,则三棱锥S-ABC的体积为
12.两个圆锥有等长的母线,它们的侧面展开图恰好拼成一个圆,若它们的侧面积之比为
1:2,则它们的体积比为
13.在《九章算术》中,将底面为直角三角形,侧棱垂直于底面的三棱柱称之为堑堵,如图
在堑堵ABC-ABC1中,AB=BC,AA>AB,堑堵的顶点C1到直线AC的距离为
C到平面A1BC的距离为n,则一的取值范围是
B
14.如图,在长方体ABCD-ABCD中,AD=D=1,AB=√3,E、F、G分别为
AB、BC、C1D的中点,点P在平面ABCD内,若直线DP∥平面EFG,则线段DP长
度的最小值是
选择题(共有6题,满分30分,每题5分
15.在空间内,异面直线所成角的取值范围是()
B.(0,
C.[0,-)
D.[0,-]
D是某长方体四条棱的中点,
则直线AB和直线CD的位置关系是()
A.相交
B.平行
异面
D.垂直
17.设a、b是平面M外的两条直线,且a∥M,
那么a∥b是b∥M的
条件
A.充分非必要
B.必要非充分
C.充要
D.非充分非必要
18.已知异面直线a、b所成角为80°,P为空间一定点,则过P点且与a、b所成角都
是50°的直线有且仅有()条
B.3
D.6
19.已知直线a,如果直线b同时满足:(1)与a异面;(2)与a所成的角是108°;(3)
与a的距离为2021,这样的直线b有()条
B
20.在空间中,过点A作平面z的垂线,垂足为B,记B=f(A),设a、B是两个不同的
平面,对空间任意一点P,Q=ff(P,Q2=fL(P,恒有PQ=PQ2,则()
同课章节目录
