3.2.2灵活运用平均数、中位数、众数解决问题-2021-2022学年苏科版九年级数学上册培优训练(Word版 含答案)
文档属性
| 名称 | 3.2.2灵活运用平均数、中位数、众数解决问题-2021-2022学年苏科版九年级数学上册培优训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 736.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 18:21:06 | ||
图片预览



文档简介
3.2.2灵活运用平均数、中位数、众数解决问题
-21-22苏科版九年级数学上册 培优训练
一、选择题
1、为了调查某校学生课后参加体育锻炼的时间,学校体育组随机抽样调查了若干名学生的每天锻炼时间,统计如表:
每天锻炼时间(分钟) 20 40 60 80
学生数(人) 2 3 4 1
下列说法错误的是( )
A.众数是60分钟 B.平均数是52.5分钟 C.样本容量是10 D.中位数是50分钟
2、某校对进校学生进行体温检测,在某一时段测得6名学生的体温分别为36.8℃,36.9℃,36.5℃,36.6℃,36.9℃,36.5℃,那么这6名学生体温的平均数与中位数分别是( )
A.36.7℃,36.7℃ B.36.6℃,36.8℃
C.36.8℃,36.7℃ D.36.7℃,36.8℃
3、某校为了了解七年级学生的身高情况(单位:cm,精确到1cm),抽查了部分学生,将所得数据处理后分成七组(每组只含最低值,不含最高值),并制成下列两个图表(部分):
分组 一 二 三 四 五 六 七
104﹣145 145﹣150 150﹣155 155﹣160 160﹣165 165﹣170 170﹣175
人数 6 12 26 4
根据以上信息可知,样本的中位数落在( )
A.第二组 B.第三组 C.第四组 D.第五组
4、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
5、在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
年龄(岁) 18 22 30 35 43
人数 2 3 2 2 1
则这10名队员年龄的中位数、众数分别是( )
A.20岁,35岁 B.22岁,22岁 C.26岁、22岁 D.30岁,30岁
6、某车间20名工人每天加工零件数如下表所示:
每天加工零件数 4 5 6 7 8
人数 3 6 5 4 2
这些工人每天加工零件数的众数、中位数分别是( ).
A.5,5 B.5,6 C.6,6 D.6,5
7、为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:则关于这些同学的每天锻炼时间,下列说法错误的是
每天锻炼事件(分钟)
学生数
A.平均数是 B.众数是
C.抽查了个同学 D.中位数是
8、小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是( )
A.中位数是3,众数是2 B.众数是1,平均数是2
C.中位数是2,众数是2 D.中位数是3,平均数是2.5
9、某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是( )
A.50,48 B.48,49 C.50,49 D.48,48
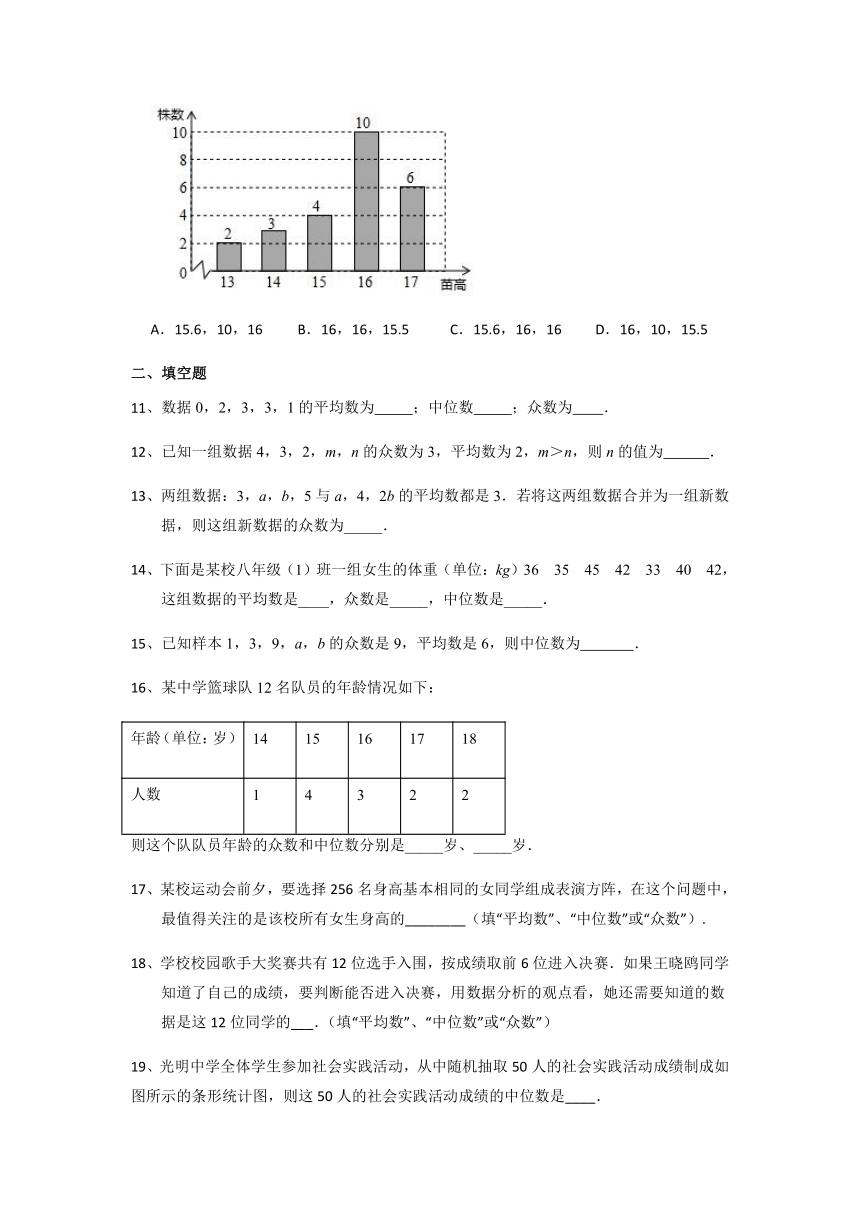
10、农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高进行了测量,根据统计的结果,绘制出如下的统计图.则统计的这组苗高数据的平均数、众数、中位数依次是( )
A.15.6,10,16 B.16,16,15.5 C.15.6,16,16 D.16,10,15.5
二、填空题
11、数据0,2,3,3,1的平均数为 ;中位数 ;众数为 .
12、已知一组数据4,3,2,m,n的众数为3,平均数为2,m>n,则n的值为 .
13、两组数据:3,a,b,5与a,4,2b的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为_____.
14、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
15、已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为 .
16、某中学篮球队12名队员的年龄情况如下:
年龄(单位:岁) 14 15 16 17 18
人数 1 4 3 2 2
则这个队队员年龄的众数和中位数分别是_____岁、_____岁.
17、某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
18、学校校园歌手大奖赛共有12位选手入围,按成绩取前6位进入决赛.如果王晓鸥同学知道了自己的成绩,要判断能否进入决赛,用数据分析的观点看,她还需要知道的数据是这12位同学的___.(填“平均数”、“中位数”或“众数”)
19、光明中学全体学生参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,则这50人的社会实践活动成绩的中位数是____.
20、为了了解用电量的多少,李明在6月初的连续几天同一时刻观察电表显示的度数记录如下:
日期 1号 2号 3号 4号 5号 6号 7号 8号
电表显示 217 222 228 234 239 242 248 252
估计李明家6月份的用电总量是________度.
三、解答题
21、某手表厂为了解生产的某种型号手表的质量,随机抽检了部分该型号手表的日走时误差,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(1)本次抽检的该型号手表的只数为_______,图①中的m的值为______;
(2)求本次抽检获取的样本数据的众数、中位数和平均数;
(3)若该手表厂每月生产该型号手表200只,估计其中日走时误差小于的只数.
22、某工厂第一车间有工人20人,每人日均加工螺杆数统计如图.
第一车间工人日均生产能力统计图
请根据以上提供的信息解答下列问题:
(1)该车间工人日均生产螺杆数的平均数、中位数和众数分别是多少?
(2)若要从平均数、中位数、众数中选一个作为该车间工人日生产定额,超额部分给予奖励.为鼓励大多数工人,你认为选哪个统计量比较合适,请说明理由.
23、为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 5 2 1 3 1
数据分析:样本数据的平均数、众数和中位数如表:
平均数 中位数 众数
93
(1) , , , ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数和中位数如表:
平均数 中位数 众数
95 93 94
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
24、某校名学生参加植树活动,要求每人植树的范围是棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:棵;B:棵;C:棵;D:棵,将各类的人数绘制成扇形统计图(如图2)和条形统计图(如图1).回答下列问题:
(1)在这次调查中类型有多少名学生?并补全条形统计图;
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这名学生共植树多少棵?
25、编号为号的名学生进行定点投篮,规定每人投次,每命中次记分,没有命中记分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第号学生也按同样记分规定投了次,其命中率为.
(1)第号学生的积分为 分
(2)这名学生积分的中位数为 分,众数为 分.
(3)若又来了第号学生,也按同样记分规定投了次,这时加入号学生的得分后,众数发生了改变,同时平均数变大了,求此时名学生积分的众数.
26、为了解某校九年级学生的理化实验操作情况,随机抽查40名同学实验操作的得分(满分为10分).根据获取的样本数据,制作了如图的条形统计图和扇形统计图,请根据相关信息解答下列问题.
(1)①中的描述应为“6分”,其中m的值为________;扇形①的圆心角的大小是________;
(2)这40个样本数据平均数是________,众数是________,中位数是________;
(3)若该校九年级共有1280名学生,估计该校理化实验操作得满分的学生有多少人.
27、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
3.2.2灵活运用平均数、中位数、众数解决问题
-21-22苏科版九年级数学上册 培优训练(有答案)
一、选择题
1、为了调查某校学生课后参加体育锻炼的时间,学校体育组随机抽样调查了若干名学生的每天锻炼时间,统计如表:
每天锻炼时间(分钟) 20 40 60 80
学生数(人) 2 3 4 1
下列说法错误的是( )
A.众数是60分钟 B.平均数是52.5分钟 C.样本容量是10 D.中位数是50分钟
【答案】B
【分析】根据已知数据,分析出众数,中位数,样本容量,平均数即可得到结论.
【详解】解:根据统计表可得,众数是60分钟;中位数是第5,6个数平均数即:50分钟;样本容量是10;
故A、C、D三个选项都正确,
所以B选项错误
故选B.
2、某校对进校学生进行体温检测,在某一时段测得6名学生的体温分别为36.8℃,36.9℃,36.5℃,36.6℃,36.9℃,36.5℃,那么这6名学生体温的平均数与中位数分别是( )
A.36.7℃,36.7℃ B.36.6℃,36.8℃
C.36.8℃,36.7℃ D.36.7℃,36.8℃
【答案】A
【分析】根据平均数的求法,求出平均数即可,然后将这组数据从新排列,再根据中位数和平均数的定义求解即可.
【详解】解:将这组数据重新排列为36.5℃,36.5℃,36.6℃,36.8℃,36.9℃,36.9℃,
∴这组数据的平均数为,
中位数为,
故选:A.
3、某校为了了解七年级学生的身高情况(单位:cm,精确到1cm),抽查了部分学生,将所得数据处理后分成七组(每组只含最低值,不含最高值),并制成下列两个图表(部分):
分组 一 二 三 四 五 六 七
104﹣145 145﹣150 150﹣155 155﹣160 160﹣165 165﹣170 170﹣175
人数 6 12 26 4
根据以上信息可知,样本的中位数落在( )
A.第二组 B.第三组 C.第四组 D.第五组
【答案】C
【分析】从表格和扇形图上可知第二组的12人占了总数的12%,从而求出第三组人数;第五组为24人,第六组为10人,中位数应该是第50和51个数的平均数,从表格可知第50和51个数落在第四组中.
【详解】解:总数为12÷12%=100人,
第三组人数为100×18%=18人,
中位数应该是第50和51个数的平均数,
从表格可知第50和51个数落在第四组中.
答案:C.
4、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
【答案】C
【分析】根据众数和中位数的定义,结合所给数据即可得出答案.
【详解】解:将这组数据按从小到大的顺序排列为:29,30,30,32,32,32,
出现最多的数字为:32,故众数是32,
中位数为第3、4个数的平均数,即为.
故选:C.
5、在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
年龄(岁) 18 22 30 35 43
人数 2 3 2 2 1
则这10名队员年龄的中位数、众数分别是( )
A.20岁,35岁 B.22岁,22岁 C.26岁、22岁 D.30岁,30岁
【答案】C
【分析】分别根据中位数和众数的概念计算即可.
【详解】中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.这10个数据处于中间位置的是22,30,所以中位数是;
众数:一组数据中出现次数最多的数据为这组数据的众数.10个数据中22出现了3次,次数最多,所以众数是22,
故选:C.
6、某车间20名工人每天加工零件数如下表所示:
每天加工零件数 4 5 6 7 8
人数 3 6 5 4 2
这些工人每天加工零件数的众数、中位数分别是( ).
A.5,5 B.5,6 C.6,6 D.6,5
【答案】B
【分析】根据众数、中位数的定义分别进行解答即可.
【详解】解:由表知数据5出现次数最多,所以众数为5;
因为共有20个数据,
所以中位数为第10、11个数据的平均数,即中位数为=6,
故选:B.
7、为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:则关于这些同学的每天锻炼时间,下列说法错误的是
每天锻炼事件(分钟)
学生数
A.平均数是 B.众数是
C.抽查了个同学 D.中位数是
【答案】A
【分析】根据众数、中位数和平均数的定义分别对每一项进行分析即可.
【详解】解:A、这组数据的平均数是:(20×2+40×3+60×4+90×1)÷10=49,原来的说法错误,符合题意;
B、60出现了4次,出现的次数最多,则众数是60的说法正确,不符合题意;
C、调查的学生数是2+3+4+1=10,故说法正确,不符合题意;
D、把这组数据从小到大排列,最中间的两个数的平均数是(40+60)÷2=50,则中位数是50,故说法正确,不符合题意.
故选:A.
8、小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是( )
A.中位数是3,众数是2 B.众数是1,平均数是2
C.中位数是2,众数是2 D.中位数是3,平均数是2.5
【答案】C
【分析】根据统计图中的数据,求出中位数,平均数,众数,即可做出判断.
【详解】解:15名同学一周的课外阅读量为0,1,1,1,1,2,2,2,2,2,2,3,3,4,4,
中位数为2;
平均数为(0×1+1×4+2×6+3×2+4×2)÷15=2;
众数为2;
故选:C.
9、某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是( )
A.50,48 B.48,49 C.50,49 D.48,48
【分析】先根据折线统计图将这组数据重新排列,再根据众数和中位数的概念求解即可.
【解析】由折线统计图得出这6个数据(从小到大排列)为47、47、48、48、48、50,
所以这组数据的众数为48,中位数为=48,
故选:D.
10、农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高进行了测量,根据统计的结果,绘制出如下的统计图.则统计的这组苗高数据的平均数、众数、中位数依次是( )
A.15.6,10,16 B.16,16,15.5 C.15.6,16,16 D.16,10,15.5
【分析】根据平均数、众数和中位数的定义直接进行解答即可.
【解析】这组苗高数据的平均数是
∵16出现了10次,出现的次数最多,
∴众数是16,
把这些数从小大排列,中位数是第13个数,
则中位数是16.
故选:C.
二、填空题
11、数据0,2,3,3,1的平均数为 ;中位数 ;众数为 .
【答案】,2,3.
【解析】解:这组数据的平均数为=,
重新排列为0、1、2、3、3,
所以中位数为2,众数为3,
故答案为:,2,3.
12、已知一组数据4,3,2,m,n的众数为3,平均数为2,m>n,则n的值为 .
【答案】-2
【解析】解:∵一组数据4,3,2,m,n的众数为3,平均数为2,m>n,
∴m=3,
∴4+3+2+3+n=2×5,
解得n=﹣2.
故答案为:﹣2.
13、两组数据:3,a,b,5与a,4,2b的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为_____.
【答案】3
【分析】根据平均数的意义,求出a、b的值,进而确定两组数据,再合并成一组,找出出现次数最多的数据即可.
【详解】解:由题意得,,解得,
这两组数据为:3、3、1、5和3、4、2,这两组数合并成一组新数据,
在这组新数据中,出现次数最多的是3,因此众数是3,
故答案为:3.
14、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
【答案】
【分析】分别利用平均数、众数及中位数的定义求解后即可得出答案.
【详解】解:将数据重新排列为33、35、36、40、42、42、45,
所以这组数据的平均数为,
众数为、中位数为,
故答案为:、、.
15、已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为 .
【答案】8
【解析】解:∵样本1,3,9,a,b的众数是9,
∴a,b中至少有一个是9,
∵样本1,3,9,a,b的平均数为6,
∴(1+3+9+a+b)=6,
∴a+b=17,
∴a,b中一个是9,另一个是8,
∴这组数为1,3,9,8,9,
即1,3,8,9,9,
∴这组数据的中位数是8.
故答案为:8.
16、某中学篮球队12名队员的年龄情况如下:
年龄(单位:岁) 14 15 16 17 18
人数 1 4 3 2 2
则这个队队员年龄的众数和中位数分别是_____岁、_____岁.
【答案】16 15
【分析】根据中位数和众数的定义求解.
【详解】解:从小到大排列此数据,数据15出现了四次最多为众数,16和16处在第5位和第六位,它两个数的平均数为16为中位数.
故答案为:16,15.
17、某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
【答案】众数
【解析】试题分析:
根据题意:在这个问题中我们最值的关注的是队伍的整齐,身高必须差不多;
故应该关注该校所有女生身高的众数.
故答案为:众数.
18、学校校园歌手大奖赛共有12位选手入围,按成绩取前6位进入决赛.如果王晓鸥同学知道了自己的成绩,要判断能否进入决赛,用数据分析的观点看,她还需要知道的数据是这12位同学的___.(填“平均数”、“中位数”或“众数”)
【答案】中位数.
【分析】参赛选手要想知道自己是否能进入前6名,只需要了解自己的成绩与全部成绩的中位数的大小即可.
【详解】由于总共有12个人,且他们的分数互不相同,要判断是否进入前6名,只要把自己的成绩与中位数进行大小比较.故应知道中位数的多少.
故答案为中位数.
19、光明中学全体学生参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,则这50人的社会实践活动成绩的中位数是____.
【答案】4.
【分析】中位数是第25个数据与第26个数据的平均数,根据人数确定第25个数据为4,第26个数据为4,计算即可
【详解】∵50人的条形图如下,
2+9+13=24,
∴第25个数据为4,第26个数据为4,
∴中位数是=4,
故答案为:4.
20、为了了解用电量的多少,李明在6月初的连续几天同一时刻观察电表显示的度数记录如下:
日期 1号 2号 3号 4号 5号 6号 7号 8号
电表显示 217 222 228 234 239 242 248 252
估计李明家6月份的用电总量是________度.
【答案】
【分析】先求七天用电量的平均数,再利用样本平均数估计月份(天)的总用电量即可得答案.
【详解】解:号的用电量为:
号的用电量为:
同理可得:号至号的用电量分别为:,
这七天的平均用电量为:
,
故答案为:
三、解答题
21、某手表厂为了解生产的某种型号手表的质量,随机抽检了部分该型号手表的日走时误差,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(1)本次抽检的该型号手表的只数为_______,图①中的m的值为______;
(2)求本次抽检获取的样本数据的众数、中位数和平均数;
(3)若该手表厂每月生产该型号手表200只,估计其中日走时误差小于的只数.
【答案】(1)40,25;(2)众数为0.5s,中位数为0.75s,平均数是0.7s;(3)140只
【分析】(1)用0.5s的频数除以它的百分比可求抽检手表只数,用1减去其他百分比可得m的值;
(2)根据众数、中位数和平均数的定义计算即可;
(3)用200乘以误差小于的百分比即可.
【详解】解:(1)12÷30%=40(只),
1-20%-10%-15%-30%=25%,
故答案为:40,25;
(2)∵在这组数据中,0.5出现了12次,出现的次数最多,
∴这组数据的众数为0.5s.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是0.75.有(s).
∴这组数据的中位数为0.75 s;
观察条形统计图,,
∴这组数据的平均数是0.7 s.
(3)∵在抽检的40只手表中,日走时误差小于的只数占25%+30%+15%=70%,
∴估计该手表厂每月生产的200只手表中日走时误差小于的只数约占70%.
有(只).
∴该手表厂每月生产的200只手表中日走时误差小于的约为140只.
22、某工厂第一车间有工人20人,每人日均加工螺杆数统计如图.
第一车间工人日均生产能力统计图
请根据以上提供的信息解答下列问题:
(1)该车间工人日均生产螺杆数的平均数、中位数和众数分别是多少?
(2)若要从平均数、中位数、众数中选一个作为该车间工人日生产定额,超额部分给予奖励.为鼓励大多数工人,你认为选哪个统计量比较合适,请说明理由.
【答案】(1)平均数:13.4;中位数:14;众数:12;(2)众数,理由见解析
【分析】(1)根据中位数、众数及平均数的定义即可求解,
(2)根据根据中位数、众数及平均数的数值,找到一个大多数人能达到的统计量即可.
【详解】(1)某工厂第一车间有工人20人,
平均数为(10×2+12×7+14×6+16×5)÷20=13.4
按照顺序排列第10个、11个工人日均加工螺杆数分别是14、14,所以中位数为14.
日加工螺杆数为12个的有7名工人,所以众数为12;
(2)若选平均数,则超额部分给予奖励的人数为11人;
若选中位数,则超额部分给予奖励的人数为11人;
若选众数,则超额部分给予奖励的人数为11人;
又因为在众数生产额的人数较多,故为鼓励大多数工人,选众数比较合适.
23、为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 5 2 1 3 1
数据分析:样本数据的平均数、众数和中位数如表:
平均数 中位数 众数
93
(1) , , , ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数和中位数如表:
平均数 中位数 众数
95 93 94
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
【答案】(1)3;2;91;90;(2)估计评选该荣誉称号的人数为105人;(3)11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
【分析】由题意直接写出a,b的值,再根据中位数和众数的定义即可求出c,d的值;
(2)先求出测评成绩优秀的学生人数所占分率,再乘300即可得出结论.
(3)从中位数出发,结合题意即可得出结论;
【详解】
解:(1)由题意得:91分的有2个,即a=3;
98分的有2个,即b=2;
出现次数最多的是90分,故众数是90分,即d=90;
一共20个数据,第10个,第11个数据都是91,故中位数是91分,即c=91.
故答案为:3;2;91;90;
(2)300×=105(人).
答:估计评选该荣誉称号的人数为105人;
(3)10月份的中位数是91,11月份的中位数是93,
∵93>91,∴ 11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
24、某校名学生参加植树活动,要求每人植树的范围是棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:棵;B:棵;C:棵;D:棵,将各类的人数绘制成扇形统计图(如图2)和条形统计图(如图1).回答下列问题:
(1)在这次调查中类型有多少名学生?并补全条形统计图;
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这名学生共植树多少棵?
【答案】(1)2人,图见解析;(2)众数是3,中位数是3;(3)2178棵
【分析】(1)利用总人数20乘以对应的百分比即可求得D类的人数,从而补全条形统计图;
(2)根据众数、中位数的定义即可直接求解;
(3)首先求得调查的20人的平均数,乘以总人数260即可.
【详解】解:(1)由B占40%,且人数为8人,可得样本数为(人),
∴类型有人,
补全条形统计图如下:
(2)由条形统计图可得众数为3棵,中位数为第10和第11个数据的平均数,为3棵;
(3)棵,
∴这名学生共植树棵.
25、编号为号的名学生进行定点投篮,规定每人投次,每命中次记分,没有命中记分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第号学生也按同样记分规定投了次,其命中率为.
(1)第号学生的积分为 分
(2)这名学生积分的中位数为 分,众数为 分.
(3)若又来了第号学生,也按同样记分规定投了次,这时加入号学生的得分后,众数发生了改变,同时平均数变大了,求此时名学生积分的众数.
【答案】(1)7;(2)7.5,9;(3)名学生积分的众数是8,9
【分析】(1)由第6名学生命中的个数为10×=7可得答案;
(2)由这6名学生中,将得分排列找出众数和中位数即可;
(3)根据平均数得变大了找到关于第7名同学成绩的不等式,求出范围,再根据题意众数发生了改变,即可找到合适的值,进而求众数即可.
【详解】解:(1)第6名学生命中的个数为10×=7,第6号学生的积分为7分.
故答案为7.
(2)这6名学生中,按照得分由低到高的顺序排列:4,5,7,8,9,9,则中位数;
命中次数为9,则众数是9;
故答案为7.5, 9.
(3)由于前6名学生积分的平均数为: .
设第7名学生积分为x分.
由题意得:,解得:
又∵众数发生改变,∴, ∴
∴此时名学生积分的众数是8,9.
26、为了解某校九年级学生的理化实验操作情况,随机抽查40名同学实验操作的得分(满分为10分).根据获取的样本数据,制作了如图的条形统计图和扇形统计图,请根据相关信息解答下列问题.
(1)①中的描述应为“6分”,其中m的值为________;扇形①的圆心角的大小是________;
(2)这40个样本数据平均数是________,众数是________,中位数是________;
(3)若该校九年级共有1280名学生,估计该校理化实验操作得满分的学生有多少人.
【答案】(1)10;;(2)8.3;9;8;(3)224
【分析】(1)所占百分比=所求人数与总人数之比,即可求出m的值;再用乘以①所占的百分比,计算即可得解;
(2)根据平均数的定义求出平均数;众数是一组数据中出现次数最多的数据;找中位数要把数据从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数进行解答;
(3)用九年级总学生人数乘以满分的人数所占的分数即可.
【详解】解:(1),即m=10;
∴,
故答案为:10;;
(2)平均数:(分),
∵9出现了12次,次数最多,∴众数为:9分;
∵将40个数字按从小到大排列,中间第20、21两个数都是8,∴中位数为:=8(分);
故答案为:8.3分,9分,8分;
(3)(人)
答:该校理化实验操作得满分的学生有224人.
27、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
【答案】(1)20,见解析;(2)4;4;(3)平均数为5.3棵,这280名学生共植树1848棵
【分析】(1)由B类型的人数及其所占百分比可得总人数,总人数乘以D类型的对应的百分比即可求出其人数,据此可补全图形;
(2)根据众数和中位数的概念可得答案;
(3)先求出样本的平均数,再乘以总人数即可.
【详解】解:(1)这次调查一共抽查植树的学生人数为8÷40%=20(人),
D类人数=20×10%=2(人);
条形图补充如图:
故答案为:20;
(2)植树4棵的人数最多,则众数是4,
共有20人植树,其中位数是第10、11人植树数量的平均数,则中位数是4,
故答案为:4、4;
(3)(棵),
5.3×280=1484(棵).
答:估计这3280名学生共植树1484棵.
-21-22苏科版九年级数学上册 培优训练
一、选择题
1、为了调查某校学生课后参加体育锻炼的时间,学校体育组随机抽样调查了若干名学生的每天锻炼时间,统计如表:
每天锻炼时间(分钟) 20 40 60 80
学生数(人) 2 3 4 1
下列说法错误的是( )
A.众数是60分钟 B.平均数是52.5分钟 C.样本容量是10 D.中位数是50分钟
2、某校对进校学生进行体温检测,在某一时段测得6名学生的体温分别为36.8℃,36.9℃,36.5℃,36.6℃,36.9℃,36.5℃,那么这6名学生体温的平均数与中位数分别是( )
A.36.7℃,36.7℃ B.36.6℃,36.8℃
C.36.8℃,36.7℃ D.36.7℃,36.8℃
3、某校为了了解七年级学生的身高情况(单位:cm,精确到1cm),抽查了部分学生,将所得数据处理后分成七组(每组只含最低值,不含最高值),并制成下列两个图表(部分):
分组 一 二 三 四 五 六 七
104﹣145 145﹣150 150﹣155 155﹣160 160﹣165 165﹣170 170﹣175
人数 6 12 26 4
根据以上信息可知,样本的中位数落在( )
A.第二组 B.第三组 C.第四组 D.第五组
4、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
5、在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
年龄(岁) 18 22 30 35 43
人数 2 3 2 2 1
则这10名队员年龄的中位数、众数分别是( )
A.20岁,35岁 B.22岁,22岁 C.26岁、22岁 D.30岁,30岁
6、某车间20名工人每天加工零件数如下表所示:
每天加工零件数 4 5 6 7 8
人数 3 6 5 4 2
这些工人每天加工零件数的众数、中位数分别是( ).
A.5,5 B.5,6 C.6,6 D.6,5
7、为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:则关于这些同学的每天锻炼时间,下列说法错误的是
每天锻炼事件(分钟)
学生数
A.平均数是 B.众数是
C.抽查了个同学 D.中位数是
8、小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是( )
A.中位数是3,众数是2 B.众数是1,平均数是2
C.中位数是2,众数是2 D.中位数是3,平均数是2.5
9、某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是( )
A.50,48 B.48,49 C.50,49 D.48,48
10、农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高进行了测量,根据统计的结果,绘制出如下的统计图.则统计的这组苗高数据的平均数、众数、中位数依次是( )
A.15.6,10,16 B.16,16,15.5 C.15.6,16,16 D.16,10,15.5
二、填空题
11、数据0,2,3,3,1的平均数为 ;中位数 ;众数为 .
12、已知一组数据4,3,2,m,n的众数为3,平均数为2,m>n,则n的值为 .
13、两组数据:3,a,b,5与a,4,2b的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为_____.
14、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
15、已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为 .
16、某中学篮球队12名队员的年龄情况如下:
年龄(单位:岁) 14 15 16 17 18
人数 1 4 3 2 2
则这个队队员年龄的众数和中位数分别是_____岁、_____岁.
17、某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
18、学校校园歌手大奖赛共有12位选手入围,按成绩取前6位进入决赛.如果王晓鸥同学知道了自己的成绩,要判断能否进入决赛,用数据分析的观点看,她还需要知道的数据是这12位同学的___.(填“平均数”、“中位数”或“众数”)
19、光明中学全体学生参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,则这50人的社会实践活动成绩的中位数是____.
20、为了了解用电量的多少,李明在6月初的连续几天同一时刻观察电表显示的度数记录如下:
日期 1号 2号 3号 4号 5号 6号 7号 8号
电表显示 217 222 228 234 239 242 248 252
估计李明家6月份的用电总量是________度.
三、解答题
21、某手表厂为了解生产的某种型号手表的质量,随机抽检了部分该型号手表的日走时误差,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(1)本次抽检的该型号手表的只数为_______,图①中的m的值为______;
(2)求本次抽检获取的样本数据的众数、中位数和平均数;
(3)若该手表厂每月生产该型号手表200只,估计其中日走时误差小于的只数.
22、某工厂第一车间有工人20人,每人日均加工螺杆数统计如图.
第一车间工人日均生产能力统计图
请根据以上提供的信息解答下列问题:
(1)该车间工人日均生产螺杆数的平均数、中位数和众数分别是多少?
(2)若要从平均数、中位数、众数中选一个作为该车间工人日生产定额,超额部分给予奖励.为鼓励大多数工人,你认为选哪个统计量比较合适,请说明理由.
23、为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 5 2 1 3 1
数据分析:样本数据的平均数、众数和中位数如表:
平均数 中位数 众数
93
(1) , , , ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数和中位数如表:
平均数 中位数 众数
95 93 94
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
24、某校名学生参加植树活动,要求每人植树的范围是棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:棵;B:棵;C:棵;D:棵,将各类的人数绘制成扇形统计图(如图2)和条形统计图(如图1).回答下列问题:
(1)在这次调查中类型有多少名学生?并补全条形统计图;
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这名学生共植树多少棵?
25、编号为号的名学生进行定点投篮,规定每人投次,每命中次记分,没有命中记分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第号学生也按同样记分规定投了次,其命中率为.
(1)第号学生的积分为 分
(2)这名学生积分的中位数为 分,众数为 分.
(3)若又来了第号学生,也按同样记分规定投了次,这时加入号学生的得分后,众数发生了改变,同时平均数变大了,求此时名学生积分的众数.
26、为了解某校九年级学生的理化实验操作情况,随机抽查40名同学实验操作的得分(满分为10分).根据获取的样本数据,制作了如图的条形统计图和扇形统计图,请根据相关信息解答下列问题.
(1)①中的描述应为“6分”,其中m的值为________;扇形①的圆心角的大小是________;
(2)这40个样本数据平均数是________,众数是________,中位数是________;
(3)若该校九年级共有1280名学生,估计该校理化实验操作得满分的学生有多少人.
27、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
3.2.2灵活运用平均数、中位数、众数解决问题
-21-22苏科版九年级数学上册 培优训练(有答案)
一、选择题
1、为了调查某校学生课后参加体育锻炼的时间,学校体育组随机抽样调查了若干名学生的每天锻炼时间,统计如表:
每天锻炼时间(分钟) 20 40 60 80
学生数(人) 2 3 4 1
下列说法错误的是( )
A.众数是60分钟 B.平均数是52.5分钟 C.样本容量是10 D.中位数是50分钟
【答案】B
【分析】根据已知数据,分析出众数,中位数,样本容量,平均数即可得到结论.
【详解】解:根据统计表可得,众数是60分钟;中位数是第5,6个数平均数即:50分钟;样本容量是10;
故A、C、D三个选项都正确,
所以B选项错误
故选B.
2、某校对进校学生进行体温检测,在某一时段测得6名学生的体温分别为36.8℃,36.9℃,36.5℃,36.6℃,36.9℃,36.5℃,那么这6名学生体温的平均数与中位数分别是( )
A.36.7℃,36.7℃ B.36.6℃,36.8℃
C.36.8℃,36.7℃ D.36.7℃,36.8℃
【答案】A
【分析】根据平均数的求法,求出平均数即可,然后将这组数据从新排列,再根据中位数和平均数的定义求解即可.
【详解】解:将这组数据重新排列为36.5℃,36.5℃,36.6℃,36.8℃,36.9℃,36.9℃,
∴这组数据的平均数为,
中位数为,
故选:A.
3、某校为了了解七年级学生的身高情况(单位:cm,精确到1cm),抽查了部分学生,将所得数据处理后分成七组(每组只含最低值,不含最高值),并制成下列两个图表(部分):
分组 一 二 三 四 五 六 七
104﹣145 145﹣150 150﹣155 155﹣160 160﹣165 165﹣170 170﹣175
人数 6 12 26 4
根据以上信息可知,样本的中位数落在( )
A.第二组 B.第三组 C.第四组 D.第五组
【答案】C
【分析】从表格和扇形图上可知第二组的12人占了总数的12%,从而求出第三组人数;第五组为24人,第六组为10人,中位数应该是第50和51个数的平均数,从表格可知第50和51个数落在第四组中.
【详解】解:总数为12÷12%=100人,
第三组人数为100×18%=18人,
中位数应该是第50和51个数的平均数,
从表格可知第50和51个数落在第四组中.
答案:C.
4、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
【答案】C
【分析】根据众数和中位数的定义,结合所给数据即可得出答案.
【详解】解:将这组数据按从小到大的顺序排列为:29,30,30,32,32,32,
出现最多的数字为:32,故众数是32,
中位数为第3、4个数的平均数,即为.
故选:C.
5、在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
年龄(岁) 18 22 30 35 43
人数 2 3 2 2 1
则这10名队员年龄的中位数、众数分别是( )
A.20岁,35岁 B.22岁,22岁 C.26岁、22岁 D.30岁,30岁
【答案】C
【分析】分别根据中位数和众数的概念计算即可.
【详解】中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.这10个数据处于中间位置的是22,30,所以中位数是;
众数:一组数据中出现次数最多的数据为这组数据的众数.10个数据中22出现了3次,次数最多,所以众数是22,
故选:C.
6、某车间20名工人每天加工零件数如下表所示:
每天加工零件数 4 5 6 7 8
人数 3 6 5 4 2
这些工人每天加工零件数的众数、中位数分别是( ).
A.5,5 B.5,6 C.6,6 D.6,5
【答案】B
【分析】根据众数、中位数的定义分别进行解答即可.
【详解】解:由表知数据5出现次数最多,所以众数为5;
因为共有20个数据,
所以中位数为第10、11个数据的平均数,即中位数为=6,
故选:B.
7、为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:则关于这些同学的每天锻炼时间,下列说法错误的是
每天锻炼事件(分钟)
学生数
A.平均数是 B.众数是
C.抽查了个同学 D.中位数是
【答案】A
【分析】根据众数、中位数和平均数的定义分别对每一项进行分析即可.
【详解】解:A、这组数据的平均数是:(20×2+40×3+60×4+90×1)÷10=49,原来的说法错误,符合题意;
B、60出现了4次,出现的次数最多,则众数是60的说法正确,不符合题意;
C、调查的学生数是2+3+4+1=10,故说法正确,不符合题意;
D、把这组数据从小到大排列,最中间的两个数的平均数是(40+60)÷2=50,则中位数是50,故说法正确,不符合题意.
故选:A.
8、小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是( )
A.中位数是3,众数是2 B.众数是1,平均数是2
C.中位数是2,众数是2 D.中位数是3,平均数是2.5
【答案】C
【分析】根据统计图中的数据,求出中位数,平均数,众数,即可做出判断.
【详解】解:15名同学一周的课外阅读量为0,1,1,1,1,2,2,2,2,2,2,3,3,4,4,
中位数为2;
平均数为(0×1+1×4+2×6+3×2+4×2)÷15=2;
众数为2;
故选:C.
9、某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是( )
A.50,48 B.48,49 C.50,49 D.48,48
【分析】先根据折线统计图将这组数据重新排列,再根据众数和中位数的概念求解即可.
【解析】由折线统计图得出这6个数据(从小到大排列)为47、47、48、48、48、50,
所以这组数据的众数为48,中位数为=48,
故选:D.
10、农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高进行了测量,根据统计的结果,绘制出如下的统计图.则统计的这组苗高数据的平均数、众数、中位数依次是( )
A.15.6,10,16 B.16,16,15.5 C.15.6,16,16 D.16,10,15.5
【分析】根据平均数、众数和中位数的定义直接进行解答即可.
【解析】这组苗高数据的平均数是
∵16出现了10次,出现的次数最多,
∴众数是16,
把这些数从小大排列,中位数是第13个数,
则中位数是16.
故选:C.
二、填空题
11、数据0,2,3,3,1的平均数为 ;中位数 ;众数为 .
【答案】,2,3.
【解析】解:这组数据的平均数为=,
重新排列为0、1、2、3、3,
所以中位数为2,众数为3,
故答案为:,2,3.
12、已知一组数据4,3,2,m,n的众数为3,平均数为2,m>n,则n的值为 .
【答案】-2
【解析】解:∵一组数据4,3,2,m,n的众数为3,平均数为2,m>n,
∴m=3,
∴4+3+2+3+n=2×5,
解得n=﹣2.
故答案为:﹣2.
13、两组数据:3,a,b,5与a,4,2b的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为_____.
【答案】3
【分析】根据平均数的意义,求出a、b的值,进而确定两组数据,再合并成一组,找出出现次数最多的数据即可.
【详解】解:由题意得,,解得,
这两组数据为:3、3、1、5和3、4、2,这两组数合并成一组新数据,
在这组新数据中,出现次数最多的是3,因此众数是3,
故答案为:3.
14、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
【答案】
【分析】分别利用平均数、众数及中位数的定义求解后即可得出答案.
【详解】解:将数据重新排列为33、35、36、40、42、42、45,
所以这组数据的平均数为,
众数为、中位数为,
故答案为:、、.
15、已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为 .
【答案】8
【解析】解:∵样本1,3,9,a,b的众数是9,
∴a,b中至少有一个是9,
∵样本1,3,9,a,b的平均数为6,
∴(1+3+9+a+b)=6,
∴a+b=17,
∴a,b中一个是9,另一个是8,
∴这组数为1,3,9,8,9,
即1,3,8,9,9,
∴这组数据的中位数是8.
故答案为:8.
16、某中学篮球队12名队员的年龄情况如下:
年龄(单位:岁) 14 15 16 17 18
人数 1 4 3 2 2
则这个队队员年龄的众数和中位数分别是_____岁、_____岁.
【答案】16 15
【分析】根据中位数和众数的定义求解.
【详解】解:从小到大排列此数据,数据15出现了四次最多为众数,16和16处在第5位和第六位,它两个数的平均数为16为中位数.
故答案为:16,15.
17、某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
【答案】众数
【解析】试题分析:
根据题意:在这个问题中我们最值的关注的是队伍的整齐,身高必须差不多;
故应该关注该校所有女生身高的众数.
故答案为:众数.
18、学校校园歌手大奖赛共有12位选手入围,按成绩取前6位进入决赛.如果王晓鸥同学知道了自己的成绩,要判断能否进入决赛,用数据分析的观点看,她还需要知道的数据是这12位同学的___.(填“平均数”、“中位数”或“众数”)
【答案】中位数.
【分析】参赛选手要想知道自己是否能进入前6名,只需要了解自己的成绩与全部成绩的中位数的大小即可.
【详解】由于总共有12个人,且他们的分数互不相同,要判断是否进入前6名,只要把自己的成绩与中位数进行大小比较.故应知道中位数的多少.
故答案为中位数.
19、光明中学全体学生参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,则这50人的社会实践活动成绩的中位数是____.
【答案】4.
【分析】中位数是第25个数据与第26个数据的平均数,根据人数确定第25个数据为4,第26个数据为4,计算即可
【详解】∵50人的条形图如下,
2+9+13=24,
∴第25个数据为4,第26个数据为4,
∴中位数是=4,
故答案为:4.
20、为了了解用电量的多少,李明在6月初的连续几天同一时刻观察电表显示的度数记录如下:
日期 1号 2号 3号 4号 5号 6号 7号 8号
电表显示 217 222 228 234 239 242 248 252
估计李明家6月份的用电总量是________度.
【答案】
【分析】先求七天用电量的平均数,再利用样本平均数估计月份(天)的总用电量即可得答案.
【详解】解:号的用电量为:
号的用电量为:
同理可得:号至号的用电量分别为:,
这七天的平均用电量为:
,
故答案为:
三、解答题
21、某手表厂为了解生产的某种型号手表的质量,随机抽检了部分该型号手表的日走时误差,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(1)本次抽检的该型号手表的只数为_______,图①中的m的值为______;
(2)求本次抽检获取的样本数据的众数、中位数和平均数;
(3)若该手表厂每月生产该型号手表200只,估计其中日走时误差小于的只数.
【答案】(1)40,25;(2)众数为0.5s,中位数为0.75s,平均数是0.7s;(3)140只
【分析】(1)用0.5s的频数除以它的百分比可求抽检手表只数,用1减去其他百分比可得m的值;
(2)根据众数、中位数和平均数的定义计算即可;
(3)用200乘以误差小于的百分比即可.
【详解】解:(1)12÷30%=40(只),
1-20%-10%-15%-30%=25%,
故答案为:40,25;
(2)∵在这组数据中,0.5出现了12次,出现的次数最多,
∴这组数据的众数为0.5s.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是0.75.有(s).
∴这组数据的中位数为0.75 s;
观察条形统计图,,
∴这组数据的平均数是0.7 s.
(3)∵在抽检的40只手表中,日走时误差小于的只数占25%+30%+15%=70%,
∴估计该手表厂每月生产的200只手表中日走时误差小于的只数约占70%.
有(只).
∴该手表厂每月生产的200只手表中日走时误差小于的约为140只.
22、某工厂第一车间有工人20人,每人日均加工螺杆数统计如图.
第一车间工人日均生产能力统计图
请根据以上提供的信息解答下列问题:
(1)该车间工人日均生产螺杆数的平均数、中位数和众数分别是多少?
(2)若要从平均数、中位数、众数中选一个作为该车间工人日生产定额,超额部分给予奖励.为鼓励大多数工人,你认为选哪个统计量比较合适,请说明理由.
【答案】(1)平均数:13.4;中位数:14;众数:12;(2)众数,理由见解析
【分析】(1)根据中位数、众数及平均数的定义即可求解,
(2)根据根据中位数、众数及平均数的数值,找到一个大多数人能达到的统计量即可.
【详解】(1)某工厂第一车间有工人20人,
平均数为(10×2+12×7+14×6+16×5)÷20=13.4
按照顺序排列第10个、11个工人日均加工螺杆数分别是14、14,所以中位数为14.
日加工螺杆数为12个的有7名工人,所以众数为12;
(2)若选平均数,则超额部分给予奖励的人数为11人;
若选中位数,则超额部分给予奖励的人数为11人;
若选众数,则超额部分给予奖励的人数为11人;
又因为在众数生产额的人数较多,故为鼓励大多数工人,选众数比较合适.
23、为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 5 2 1 3 1
数据分析:样本数据的平均数、众数和中位数如表:
平均数 中位数 众数
93
(1) , , , ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数和中位数如表:
平均数 中位数 众数
95 93 94
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
【答案】(1)3;2;91;90;(2)估计评选该荣誉称号的人数为105人;(3)11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
【分析】由题意直接写出a,b的值,再根据中位数和众数的定义即可求出c,d的值;
(2)先求出测评成绩优秀的学生人数所占分率,再乘300即可得出结论.
(3)从中位数出发,结合题意即可得出结论;
【详解】
解:(1)由题意得:91分的有2个,即a=3;
98分的有2个,即b=2;
出现次数最多的是90分,故众数是90分,即d=90;
一共20个数据,第10个,第11个数据都是91,故中位数是91分,即c=91.
故答案为:3;2;91;90;
(2)300×=105(人).
答:估计评选该荣誉称号的人数为105人;
(3)10月份的中位数是91,11月份的中位数是93,
∵93>91,∴ 11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
24、某校名学生参加植树活动,要求每人植树的范围是棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:棵;B:棵;C:棵;D:棵,将各类的人数绘制成扇形统计图(如图2)和条形统计图(如图1).回答下列问题:
(1)在这次调查中类型有多少名学生?并补全条形统计图;
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这名学生共植树多少棵?
【答案】(1)2人,图见解析;(2)众数是3,中位数是3;(3)2178棵
【分析】(1)利用总人数20乘以对应的百分比即可求得D类的人数,从而补全条形统计图;
(2)根据众数、中位数的定义即可直接求解;
(3)首先求得调查的20人的平均数,乘以总人数260即可.
【详解】解:(1)由B占40%,且人数为8人,可得样本数为(人),
∴类型有人,
补全条形统计图如下:
(2)由条形统计图可得众数为3棵,中位数为第10和第11个数据的平均数,为3棵;
(3)棵,
∴这名学生共植树棵.
25、编号为号的名学生进行定点投篮,规定每人投次,每命中次记分,没有命中记分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第号学生也按同样记分规定投了次,其命中率为.
(1)第号学生的积分为 分
(2)这名学生积分的中位数为 分,众数为 分.
(3)若又来了第号学生,也按同样记分规定投了次,这时加入号学生的得分后,众数发生了改变,同时平均数变大了,求此时名学生积分的众数.
【答案】(1)7;(2)7.5,9;(3)名学生积分的众数是8,9
【分析】(1)由第6名学生命中的个数为10×=7可得答案;
(2)由这6名学生中,将得分排列找出众数和中位数即可;
(3)根据平均数得变大了找到关于第7名同学成绩的不等式,求出范围,再根据题意众数发生了改变,即可找到合适的值,进而求众数即可.
【详解】解:(1)第6名学生命中的个数为10×=7,第6号学生的积分为7分.
故答案为7.
(2)这6名学生中,按照得分由低到高的顺序排列:4,5,7,8,9,9,则中位数;
命中次数为9,则众数是9;
故答案为7.5, 9.
(3)由于前6名学生积分的平均数为: .
设第7名学生积分为x分.
由题意得:,解得:
又∵众数发生改变,∴, ∴
∴此时名学生积分的众数是8,9.
26、为了解某校九年级学生的理化实验操作情况,随机抽查40名同学实验操作的得分(满分为10分).根据获取的样本数据,制作了如图的条形统计图和扇形统计图,请根据相关信息解答下列问题.
(1)①中的描述应为“6分”,其中m的值为________;扇形①的圆心角的大小是________;
(2)这40个样本数据平均数是________,众数是________,中位数是________;
(3)若该校九年级共有1280名学生,估计该校理化实验操作得满分的学生有多少人.
【答案】(1)10;;(2)8.3;9;8;(3)224
【分析】(1)所占百分比=所求人数与总人数之比,即可求出m的值;再用乘以①所占的百分比,计算即可得解;
(2)根据平均数的定义求出平均数;众数是一组数据中出现次数最多的数据;找中位数要把数据从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数进行解答;
(3)用九年级总学生人数乘以满分的人数所占的分数即可.
【详解】解:(1),即m=10;
∴,
故答案为:10;;
(2)平均数:(分),
∵9出现了12次,次数最多,∴众数为:9分;
∵将40个数字按从小到大排列,中间第20、21两个数都是8,∴中位数为:=8(分);
故答案为:8.3分,9分,8分;
(3)(人)
答:该校理化实验操作得满分的学生有224人.
27、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
【答案】(1)20,见解析;(2)4;4;(3)平均数为5.3棵,这280名学生共植树1848棵
【分析】(1)由B类型的人数及其所占百分比可得总人数,总人数乘以D类型的对应的百分比即可求出其人数,据此可补全图形;
(2)根据众数和中位数的概念可得答案;
(3)先求出样本的平均数,再乘以总人数即可.
【详解】解:(1)这次调查一共抽查植树的学生人数为8÷40%=20(人),
D类人数=20×10%=2(人);
条形图补充如图:
故答案为:20;
(2)植树4棵的人数最多,则众数是4,
共有20人植树,其中位数是第10、11人植树数量的平均数,则中位数是4,
故答案为:4、4;
(3)(棵),
5.3×280=1484(棵).
答:估计这3280名学生共植树1484棵.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
