2021-2022学年苏科版七年级数学上册第四章 4.1 从问题到方程 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学上册第四章 4.1 从问题到方程 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 08:03:29 | ||
图片预览






文档简介
(共19张PPT)
4.1 从问题到方程
第4章 一元一次方程
回顾旧知
什么是方程?
方程是____________________
含有未知数的等式
例如 x+1=3 , x+1=y+2,都是方程。
下列各式中,是方程的个数为( )
(1)-4-3=-7;
(2)3x-5=2x+1;
(3)2x+6;
(4)x-y=v
(5)a+b>3;
(6)
A.1个 B.2个 C.3个 D.4个
练一练
课程讲授
1
从问题到方程
问题1:如图,天平的左盘中有两个相同的小球和
一个质量为1g的小球,右盘中有一个5g的
砝码.可以怎样来描述天平平衡时数量之
间的相等关系?
如果设两个相同小球的质量
都是xg,又能怎样描述?
设两个相同小球质量都为x,则2个的质量为2x.
天平左右两边的质量可以分别表示为 、_____,列方程即 .
(2x+1)g
5g
2x+1=5
课程讲授
问题2:篮球联赛规则规定:胜一场得2分,负一场得
1分.某篮球队赛了12场,共得20分.怎样描
述其中数量之间的相等关系?
设该队胜x场,
可以用方程2x+(12-x)=20来表示.
1
从问题到方程
则该队负(12-x)场.
新知导入
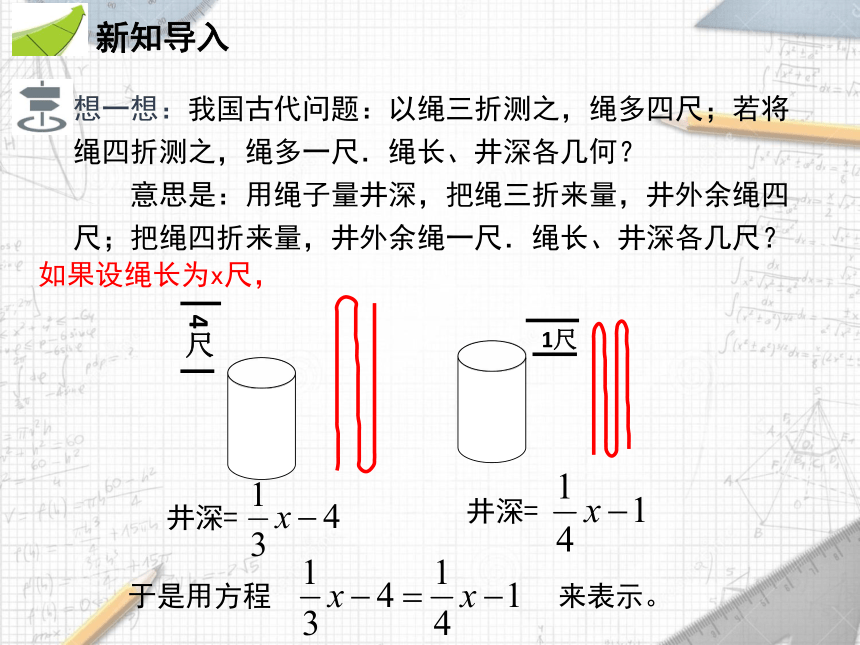
想一想:我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?
4尺
1尺
如果设绳长为x尺,
井深=
井深=
于是用方程 来表示。
课程讲授
定义:只含有一个未知数(元), 并且未知数的次数都是1(次),等号两边都是整式,像这样的方程叫做一元一次方程.
未知数次数为1
等式
未知数次数为1
等式
均只含有一个未知数
等号两边都是整式
2x+1=5
2x+(12-x)=20
1
从问题到方程
课程讲授
判断一元一次方程
特点:①只有一个未知数
例:x+y=0
2x+8=17
②未知数的次数都是1
例:
9m+1=0
③方程由整式组成(方程中分母中不能含有未知数)
例:
④未知数的系数不能为0
例:6+1=7
√
√
×
×
×
×
×
课程讲授
练一练:下列方程中是一元一次方程的是( )
A. +3=2
B. x+3=3-x
C. 1=1
D. x2=1
B
1
从问题到方程
课程讲授
例1 某校七年级共有216名师生参加某次活动,用一辆面包车和若干辆客车接送,已知一辆面包车只能坐16人,还需用多少辆40座的客车?
1
从问题到方程
提示:用方程描述下列问题中数量之间的等量关系
解:设还需用x辆40座的客车.
根据题意,得 40x+16=216.
① 设未知数
②根据题意,找等量关系,列方程。
课程讲授
例2 根据下列问题,设未知数并列出方程:
用一根长24 cm的铁丝围成一个正方形,正方形的边长是多少?
24 cm
正方形
解:设正方形的边长为x cm.
列方程:
4x=24
1
从问题到方程
课程讲授
例3 根据下列问题,设未知数并列出方程:
某校女生占全体学生数的52%,比男生多80人,这个学
校有多少学生?
解:设这个学校的学生人数为x,那么女生人数为 0.52x,男生人数为(1-0.52)x.
列方程:
0.52x-(1-0.52)x=80
1
从问题到方程
课程讲授
实际问题
设未知数
列方程
一元一次方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
1
从问题到方程
完成第98页练一练
课程讲授
练一练:1、根据“x的3倍与5的和比x的一半少2”,列出方程是( )
A.3x+5=0.5x-2
B.3x+5=0.5x+2
C.3(x+5)=0.5x-2
D.3(x+5)=0.5x+2
A
1
从问题到方程
随堂练习
2.小敏买书需要用48元,付款时恰好用了1元和5元的纸
币共12张,设所用的1元纸币为x张.根据题意,下列所
列方程正确的是( )
A.x+5(12-x)=48
B.x+5(x-12)=48
C.x+12(x-5)=48
D.5x+(12-x)=48
A
随堂练习
3.已知九年级某班30位学生种树72棵,男生每人种3棵树,女生每人种2棵树。设男生有x人,则( )
A.3x+2(30-x)=72
B.3x+2(72-x)=30
C.2x+3(30-x)=72
D.2x+3(72-x)=30
随堂练习
4.
5.
随堂练习
6.
课堂小结
从问题到方程
一元一次方程
从问题到方程
只含有一个未知数(元), 并且未知数的次数都是1(次),像这样的方程叫做一元一次方程
(1)找出等量关系;
(2)设未知量x;
(3)根据等量关系列方程
4.1 从问题到方程
第4章 一元一次方程
回顾旧知
什么是方程?
方程是____________________
含有未知数的等式
例如 x+1=3 , x+1=y+2,都是方程。
下列各式中,是方程的个数为( )
(1)-4-3=-7;
(2)3x-5=2x+1;
(3)2x+6;
(4)x-y=v
(5)a+b>3;
(6)
A.1个 B.2个 C.3个 D.4个
练一练
课程讲授
1
从问题到方程
问题1:如图,天平的左盘中有两个相同的小球和
一个质量为1g的小球,右盘中有一个5g的
砝码.可以怎样来描述天平平衡时数量之
间的相等关系?
如果设两个相同小球的质量
都是xg,又能怎样描述?
设两个相同小球质量都为x,则2个的质量为2x.
天平左右两边的质量可以分别表示为 、_____,列方程即 .
(2x+1)g
5g
2x+1=5
课程讲授
问题2:篮球联赛规则规定:胜一场得2分,负一场得
1分.某篮球队赛了12场,共得20分.怎样描
述其中数量之间的相等关系?
设该队胜x场,
可以用方程2x+(12-x)=20来表示.
1
从问题到方程
则该队负(12-x)场.
新知导入
想一想:我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?
4尺
1尺
如果设绳长为x尺,
井深=
井深=
于是用方程 来表示。
课程讲授
定义:只含有一个未知数(元), 并且未知数的次数都是1(次),等号两边都是整式,像这样的方程叫做一元一次方程.
未知数次数为1
等式
未知数次数为1
等式
均只含有一个未知数
等号两边都是整式
2x+1=5
2x+(12-x)=20
1
从问题到方程
课程讲授
判断一元一次方程
特点:①只有一个未知数
例:x+y=0
2x+8=17
②未知数的次数都是1
例:
9m+1=0
③方程由整式组成(方程中分母中不能含有未知数)
例:
④未知数的系数不能为0
例:6+1=7
√
√
×
×
×
×
×
课程讲授
练一练:下列方程中是一元一次方程的是( )
A. +3=2
B. x+3=3-x
C. 1=1
D. x2=1
B
1
从问题到方程
课程讲授
例1 某校七年级共有216名师生参加某次活动,用一辆面包车和若干辆客车接送,已知一辆面包车只能坐16人,还需用多少辆40座的客车?
1
从问题到方程
提示:用方程描述下列问题中数量之间的等量关系
解:设还需用x辆40座的客车.
根据题意,得 40x+16=216.
① 设未知数
②根据题意,找等量关系,列方程。
课程讲授
例2 根据下列问题,设未知数并列出方程:
用一根长24 cm的铁丝围成一个正方形,正方形的边长是多少?
24 cm
正方形
解:设正方形的边长为x cm.
列方程:
4x=24
1
从问题到方程
课程讲授
例3 根据下列问题,设未知数并列出方程:
某校女生占全体学生数的52%,比男生多80人,这个学
校有多少学生?
解:设这个学校的学生人数为x,那么女生人数为 0.52x,男生人数为(1-0.52)x.
列方程:
0.52x-(1-0.52)x=80
1
从问题到方程
课程讲授
实际问题
设未知数
列方程
一元一次方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
1
从问题到方程
完成第98页练一练
课程讲授
练一练:1、根据“x的3倍与5的和比x的一半少2”,列出方程是( )
A.3x+5=0.5x-2
B.3x+5=0.5x+2
C.3(x+5)=0.5x-2
D.3(x+5)=0.5x+2
A
1
从问题到方程
随堂练习
2.小敏买书需要用48元,付款时恰好用了1元和5元的纸
币共12张,设所用的1元纸币为x张.根据题意,下列所
列方程正确的是( )
A.x+5(12-x)=48
B.x+5(x-12)=48
C.x+12(x-5)=48
D.5x+(12-x)=48
A
随堂练习
3.已知九年级某班30位学生种树72棵,男生每人种3棵树,女生每人种2棵树。设男生有x人,则( )
A.3x+2(30-x)=72
B.3x+2(72-x)=30
C.2x+3(30-x)=72
D.2x+3(72-x)=30
随堂练习
4.
5.
随堂练习
6.
课堂小结
从问题到方程
一元一次方程
从问题到方程
只含有一个未知数(元), 并且未知数的次数都是1(次),像这样的方程叫做一元一次方程
(1)找出等量关系;
(2)设未知量x;
(3)根据等量关系列方程
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
