2021-2022学年人教A版(2019)选择性必修第一册3.1.2 椭圆的简单几何性质 课件(共42张)
文档属性
| 名称 | 2021-2022学年人教A版(2019)选择性必修第一册3.1.2 椭圆的简单几何性质 课件(共42张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 08:35:32 | ||
图片预览





文档简介
(共42张PPT)
3.1.2 椭圆的简单几何性质
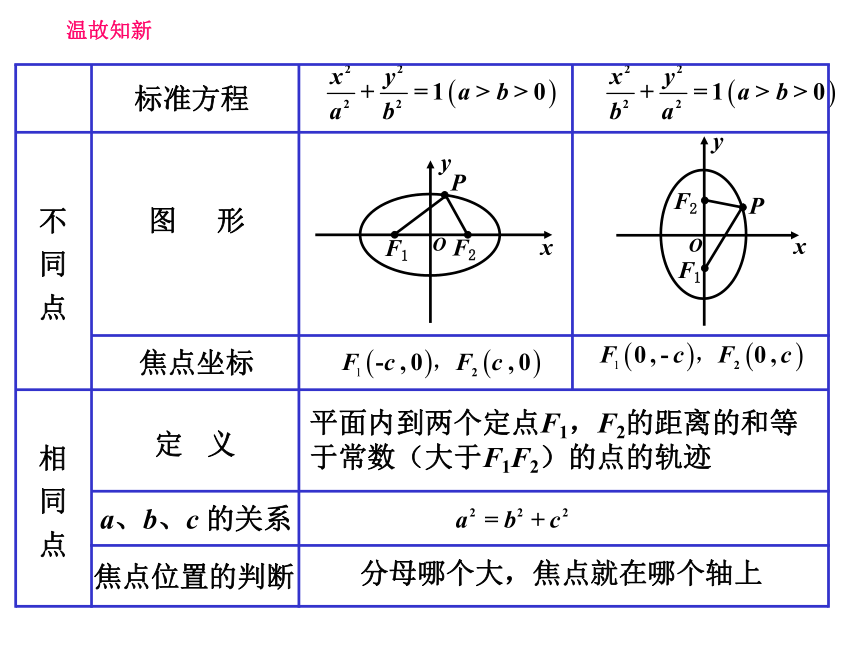
分母哪个大,焦点就在哪个轴上
平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹
标准方程
不 同 点
相 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
焦点位置的判断
x
y
F1
F2
P
O
x
y
F1
F2
P
O
温故知新
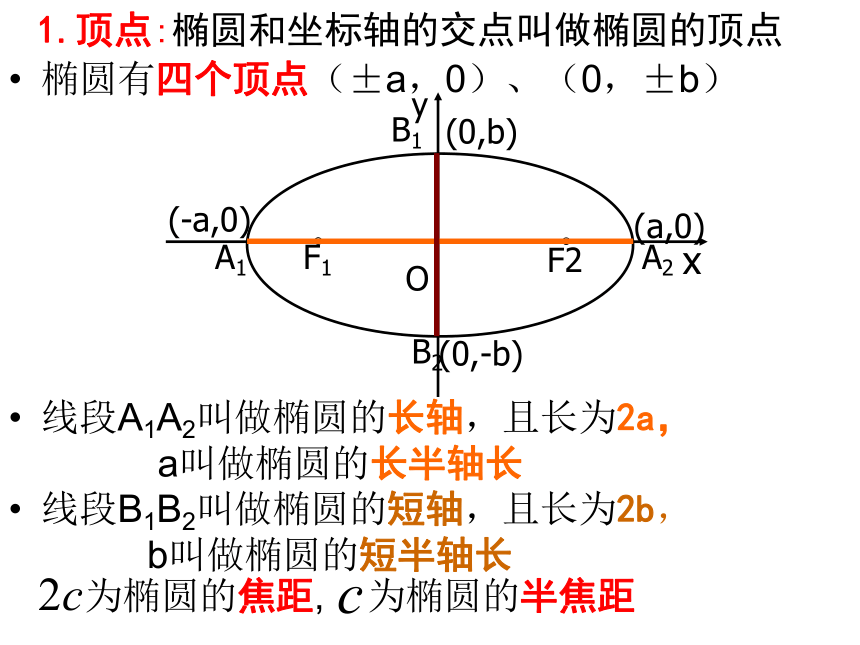
1.顶点:椭圆和坐标轴的交点叫做椭圆的顶点
椭圆有四个顶点(±a,0)、(0,±b)
线段A1A2叫做椭圆的长轴,且长为2a,
a叫做椭圆的长半轴长
线段B1B2叫做椭圆的短轴,且长为2b,
b叫做椭圆的短半轴长
O
x
F1
F2
A2
B1
B2
y
A1
(-a,0)
(a,0)
(0,b)
(0,-b)
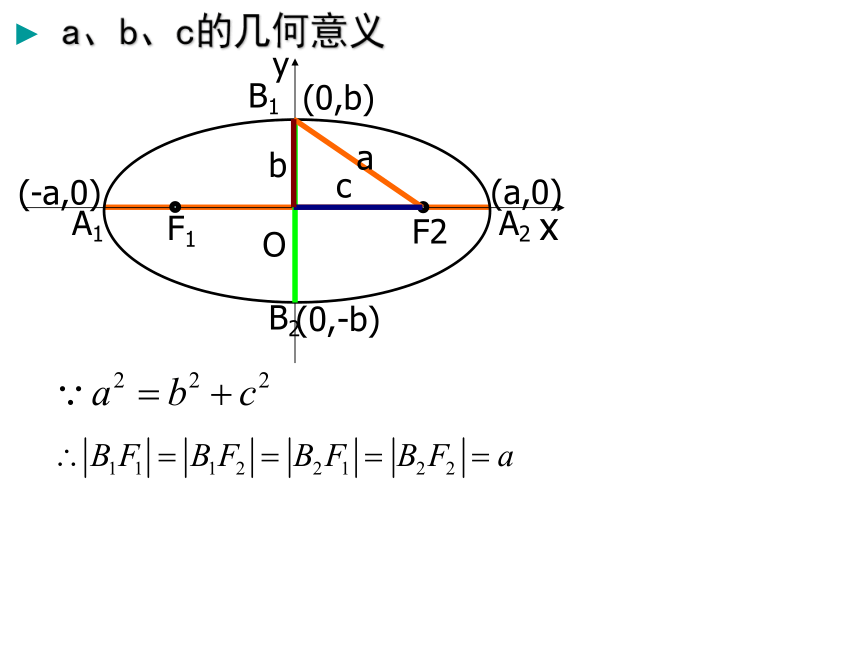
为椭圆的焦距, 为椭圆的半焦距
O
x
F1
A2
B1
B2
y
A1
(-a,0)
(a,0)
(0,b)
(0,-b)
a、b、c的几何意义
a
c
b
F2
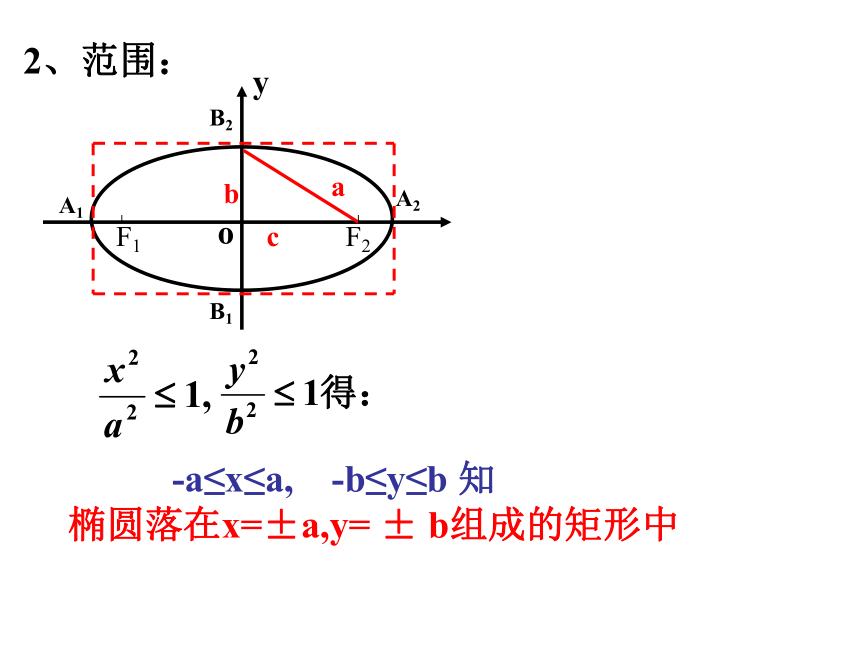
-a≤x≤a, -b≤y≤b 知
椭圆落在x=±a,y= ± b组成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
2、范围:
3、对称性:
o
y
B2
B1
A1
A2
F1
F2
c
a
b
从图形上看,椭圆关于x轴、y轴、原点对称,
原点是椭圆的中心.
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。
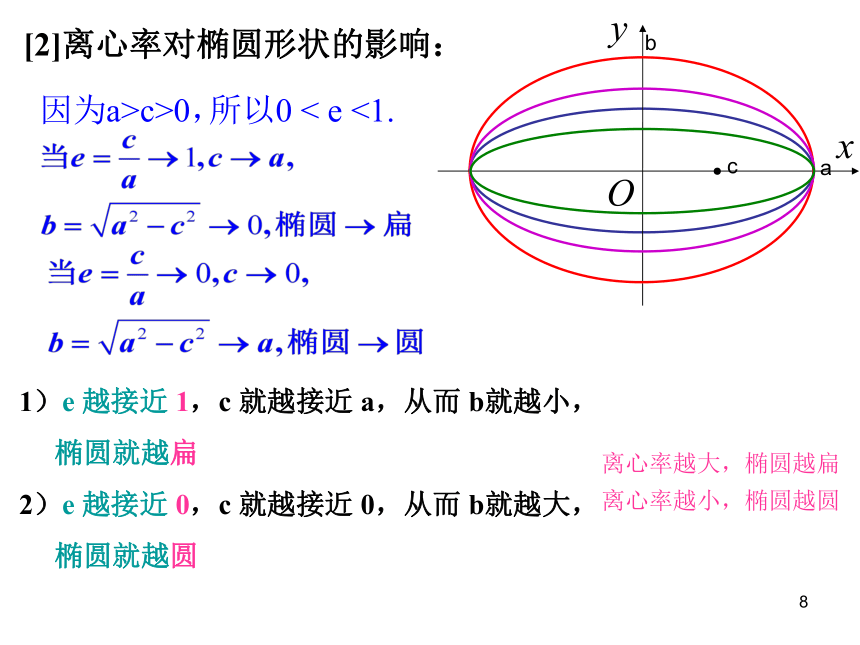
4、椭圆的离心率e(刻画椭圆扁平程度的量)
离心率:椭圆的焦距与长轴长的比:
叫做椭圆的离心率。
[1]离心率的取值范围:
0*
因为a>c>0,
所以0 < e <1.
离心率越大,椭圆越扁
离心率越小,椭圆越圆
O
x
y
a
b
●
c
[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,从而 b就越小,
椭圆就越扁
2)e 越接近 0,c 就越接近 0,从而 b就越大,
椭圆就越圆
*
思考:当e=0时,曲线是什么?当e=1时曲线又是 什么?
如果a=b,则c=0,两个焦点重合,
椭圆的标准方程就变为圆的方程:
e=0,这时两个焦点重合,图形变为圆.
e=1,为线段。
[3]e与a,b的关系:
*
方程
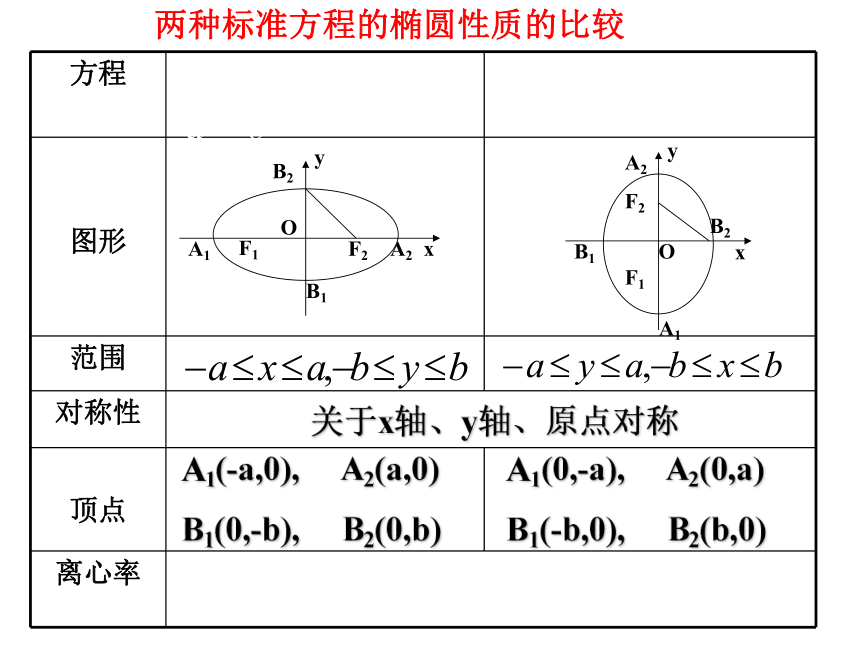
图形
范围
对称性
顶点
离心率
x
A2
B2
F2
y
O
A1
B1
F1
y
O
A1
B1
x
A2
B2
F1
F2
两种标准方程的椭圆性质的比较
关于x轴、y轴、原点对称
A1(-a,0), A2(a,0)
B1(0,-b), B2(0,b)
A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)
小试身手:
2.说出椭圆 的范围,长轴
长,短轴长,焦点坐标,顶点坐标:
练习:
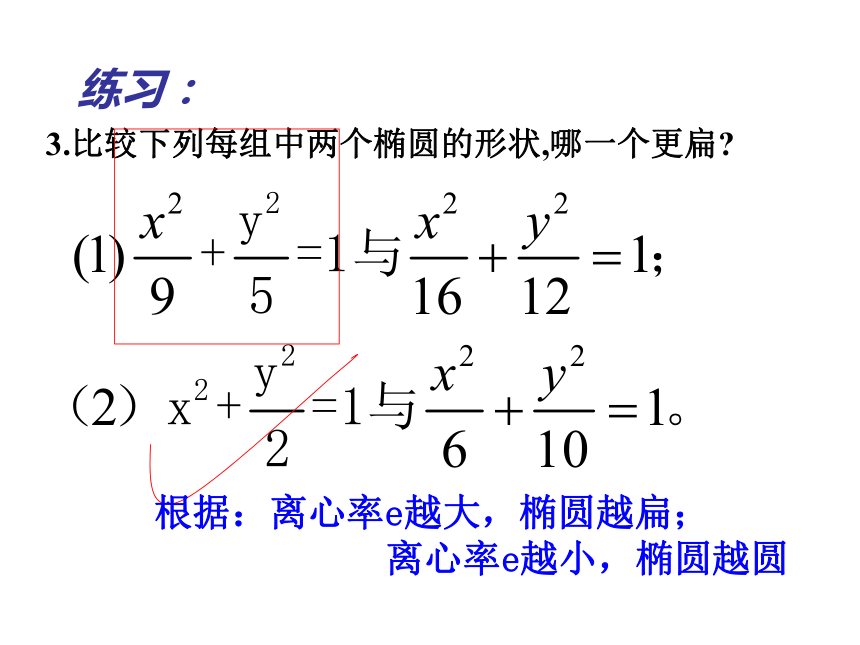
3.比较下列每组中两个椭圆的形状,哪一个更扁
根据:离心率e越大,椭圆越扁;
离心率e越小,椭圆越圆
解:
待定系数法
解:
x
y
.
F
H
O
M
求轨迹方程的步骤?
所以,点M 的轨迹是长轴长、短轴长分别为10、6的椭圆.
已知椭圆的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定椭圆方程的形式;
(2)确立关于a,b,c的方程(组),求出参数
a,b,c;
(3)写出标准方程.
【总结提升】
问题2:怎么判断它们之间的位置关系?
问题1:直线与圆的位置关系有哪几种?
d>r
dd=r
>0
<0
=0
几何法:
代数法:
直线与椭圆有什么样的位置关系,该如何判断呢?
思考:
种类:
相离(没有交点)
相切(一个交点)
相交(两个交点)
能用几何法判断椭圆与直线的位置关系吗?
探究3 直线与椭圆的位置关系
问题3:直线与椭圆的位置关系如何判定?
代数方法,联立方程
转化思想方程思想
1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程,消元得到一元二次方程(当二次项系数不为0时)
(1)△>0 直线与椭圆相交 有两个公共点;
(2)△=0 直线与椭圆相切 有且只有一个
公共点;
(3)△<0 直线与椭圆相离 无公共点.
通法
【总结提升】
直线与椭圆的位置关系:
x
o
y
分析:作出直线l及椭圆(如图),
观察图形,可以发现,利用平行于
直线l且与椭圆只有一个交点的
直线,可以求得相应的最小距离.
解:由直线l的方程与椭圆的方程可以知道,直线l与椭
圆不相交.设直线m平行于直线l,则直线m的方程可以
写成
①
②
令方程②的根的判别式△=0,得
③
解方程③,得
最大的距离是多少?
*
例4已知椭圆方程为16x2+25y2=400,
10
8
6
80
分析:椭圆方程转化为标准方程为:
a=5 b=4 c=3
o
x
y
o
x
y
它的长轴长是: 。短轴长是: 。
焦距是 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。
<例题5>求适合下列条件的椭圆的标准方程
(1) a=6, e= , 焦点在x轴上
(2) 离心率 e=0.8, 焦距为8
求椭圆的标准方程时, 应:
先定位(焦点), 再定量(a、b)
当焦点位置不确定时,要讨论,此时有两个解!
练习2:过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .
课前练习1
练习 求经过点P (4, 1),且长轴长是短轴
长的2倍的椭圆的标准方程.
解:
例题6
求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标,并画出它的图形.
解:
把方程化为标准方程
所以a=5 ,b=4
C=
所以,焦点坐标为(-3,0),(3,0)
顶点坐标为(-5,0)(5,0)(0,4)(0,-4)
2a=10,2b=8
注意:强调长轴=2a
短轴=2b
X
Y
O
例6 求符合下列条件的椭圆的标准方程:
(1)经过点(-3,0)、(0,-2);
(2)长轴的长等于20,离心率等于0.6
解: (1)由椭圆的几何性质可知,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点,所以P、Q是椭圆的顶点,
∴a=3,b=2
又因为长轴在x轴上,所以椭圆的标准方程为
(2)由以知,
2a=20,e=0.6
∴a=10,c=6
∴b=8
因为椭圆的焦点可能在x轴上,也可能在y轴上,所以所求椭圆的标准方程为:
或
你做对了吗
例2.求适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .
例3 椭圆的一个顶点为 ,其长轴长是短轴长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置
椭圆的标准方程为: ;
椭圆的标准方程为: ;
解:(1)当 为长轴端点时, , ,
(2)当 为短轴端点时, , ,
综上所述,椭圆的标准方程是 或
已知椭圆 的离心率 ,求 的值
由 ,得:
解:当椭圆的焦点在 轴上时,
, ,得 .
当椭圆的焦点在 轴上时,
, ,得 .
由 ,得 ,即 .
∴满足条件的 或 .
思考:
【变式与拓展】
3.从椭圆短轴的一个端点看长轴两端点的视角为 120°,则
此椭圆的离心率 e 为(
)
D
例5 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1出发的光线,经过旋转椭圆面反射后集中到另一个焦点F2.
解:建立如图所示的直角坐标系,
设所求椭圆方程为
y
F2
F1
x
o
B
C
A
所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。
F
l
x
o
y
M
H
d
相离
相切
相交
方程组无解
方程组有一组解
方程组有两组解
8.交点问题
设椭圆的方程为:
直线的方程为:
如何求椭圆与直线的交点呢?
联立椭圆与直线的方程得:
<0
=0
>0
9.点与椭圆的位置关系
10.弦长问题
若直线 与椭圆 的
交点为 则|AB|叫做弦长。
弦长公式:
3.1.2 椭圆的简单几何性质
分母哪个大,焦点就在哪个轴上
平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹
标准方程
不 同 点
相 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
焦点位置的判断
x
y
F1
F2
P
O
x
y
F1
F2
P
O
温故知新
1.顶点:椭圆和坐标轴的交点叫做椭圆的顶点
椭圆有四个顶点(±a,0)、(0,±b)
线段A1A2叫做椭圆的长轴,且长为2a,
a叫做椭圆的长半轴长
线段B1B2叫做椭圆的短轴,且长为2b,
b叫做椭圆的短半轴长
O
x
F1
F2
A2
B1
B2
y
A1
(-a,0)
(a,0)
(0,b)
(0,-b)
为椭圆的焦距, 为椭圆的半焦距
O
x
F1
A2
B1
B2
y
A1
(-a,0)
(a,0)
(0,b)
(0,-b)
a、b、c的几何意义
a
c
b
F2
-a≤x≤a, -b≤y≤b 知
椭圆落在x=±a,y= ± b组成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
2、范围:
3、对称性:
o
y
B2
B1
A1
A2
F1
F2
c
a
b
从图形上看,椭圆关于x轴、y轴、原点对称,
原点是椭圆的中心.
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。
4、椭圆的离心率e(刻画椭圆扁平程度的量)
离心率:椭圆的焦距与长轴长的比:
叫做椭圆的离心率。
[1]离心率的取值范围:
0
因为a>c>0,
所以0 < e <1.
离心率越大,椭圆越扁
离心率越小,椭圆越圆
O
x
y
a
b
●
c
[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,从而 b就越小,
椭圆就越扁
2)e 越接近 0,c 就越接近 0,从而 b就越大,
椭圆就越圆
*
思考:当e=0时,曲线是什么?当e=1时曲线又是 什么?
如果a=b,则c=0,两个焦点重合,
椭圆的标准方程就变为圆的方程:
e=0,这时两个焦点重合,图形变为圆.
e=1,为线段。
[3]e与a,b的关系:
*
方程
图形
范围
对称性
顶点
离心率
x
A2
B2
F2
y
O
A1
B1
F1
y
O
A1
B1
x
A2
B2
F1
F2
两种标准方程的椭圆性质的比较
关于x轴、y轴、原点对称
A1(-a,0), A2(a,0)
B1(0,-b), B2(0,b)
A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)
小试身手:
2.说出椭圆 的范围,长轴
长,短轴长,焦点坐标,顶点坐标:
练习:
3.比较下列每组中两个椭圆的形状,哪一个更扁
根据:离心率e越大,椭圆越扁;
离心率e越小,椭圆越圆
解:
待定系数法
解:
x
y
.
F
H
O
M
求轨迹方程的步骤?
所以,点M 的轨迹是长轴长、短轴长分别为10、6的椭圆.
已知椭圆的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定椭圆方程的形式;
(2)确立关于a,b,c的方程(组),求出参数
a,b,c;
(3)写出标准方程.
【总结提升】
问题2:怎么判断它们之间的位置关系?
问题1:直线与圆的位置关系有哪几种?
d>r
d
>0
<0
=0
几何法:
代数法:
直线与椭圆有什么样的位置关系,该如何判断呢?
思考:
种类:
相离(没有交点)
相切(一个交点)
相交(两个交点)
能用几何法判断椭圆与直线的位置关系吗?
探究3 直线与椭圆的位置关系
问题3:直线与椭圆的位置关系如何判定?
代数方法,联立方程
转化思想方程思想
1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程,消元得到一元二次方程(当二次项系数不为0时)
(1)△>0 直线与椭圆相交 有两个公共点;
(2)△=0 直线与椭圆相切 有且只有一个
公共点;
(3)△<0 直线与椭圆相离 无公共点.
通法
【总结提升】
直线与椭圆的位置关系:
x
o
y
分析:作出直线l及椭圆(如图),
观察图形,可以发现,利用平行于
直线l且与椭圆只有一个交点的
直线,可以求得相应的最小距离.
解:由直线l的方程与椭圆的方程可以知道,直线l与椭
圆不相交.设直线m平行于直线l,则直线m的方程可以
写成
①
②
令方程②的根的判别式△=0,得
③
解方程③,得
最大的距离是多少?
*
例4已知椭圆方程为16x2+25y2=400,
10
8
6
80
分析:椭圆方程转化为标准方程为:
a=5 b=4 c=3
o
x
y
o
x
y
它的长轴长是: 。短轴长是: 。
焦距是 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。
<例题5>求适合下列条件的椭圆的标准方程
(1) a=6, e= , 焦点在x轴上
(2) 离心率 e=0.8, 焦距为8
求椭圆的标准方程时, 应:
先定位(焦点), 再定量(a、b)
当焦点位置不确定时,要讨论,此时有两个解!
练习2:过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .
课前练习1
练习 求经过点P (4, 1),且长轴长是短轴
长的2倍的椭圆的标准方程.
解:
例题6
求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标,并画出它的图形.
解:
把方程化为标准方程
所以a=5 ,b=4
C=
所以,焦点坐标为(-3,0),(3,0)
顶点坐标为(-5,0)(5,0)(0,4)(0,-4)
2a=10,2b=8
注意:强调长轴=2a
短轴=2b
X
Y
O
例6 求符合下列条件的椭圆的标准方程:
(1)经过点(-3,0)、(0,-2);
(2)长轴的长等于20,离心率等于0.6
解: (1)由椭圆的几何性质可知,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点,所以P、Q是椭圆的顶点,
∴a=3,b=2
又因为长轴在x轴上,所以椭圆的标准方程为
(2)由以知,
2a=20,e=0.6
∴a=10,c=6
∴b=8
因为椭圆的焦点可能在x轴上,也可能在y轴上,所以所求椭圆的标准方程为:
或
你做对了吗
例2.求适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .
例3 椭圆的一个顶点为 ,其长轴长是短轴长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置
椭圆的标准方程为: ;
椭圆的标准方程为: ;
解:(1)当 为长轴端点时, , ,
(2)当 为短轴端点时, , ,
综上所述,椭圆的标准方程是 或
已知椭圆 的离心率 ,求 的值
由 ,得:
解:当椭圆的焦点在 轴上时,
, ,得 .
当椭圆的焦点在 轴上时,
, ,得 .
由 ,得 ,即 .
∴满足条件的 或 .
思考:
【变式与拓展】
3.从椭圆短轴的一个端点看长轴两端点的视角为 120°,则
此椭圆的离心率 e 为(
)
D
例5 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1出发的光线,经过旋转椭圆面反射后集中到另一个焦点F2.
解:建立如图所示的直角坐标系,
设所求椭圆方程为
y
F2
F1
x
o
B
C
A
所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。
F
l
x
o
y
M
H
d
相离
相切
相交
方程组无解
方程组有一组解
方程组有两组解
8.交点问题
设椭圆的方程为:
直线的方程为:
如何求椭圆与直线的交点呢?
联立椭圆与直线的方程得:
<0
=0
>0
9.点与椭圆的位置关系
10.弦长问题
若直线 与椭圆 的
交点为 则|AB|叫做弦长。
弦长公式:
