2021-2022学年人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共30张PPT)
文档属性
| 名称 | 2021-2022学年人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 19:25:09 | ||
图片预览






文档简介
(共30张PPT)
3.2.1双曲线及其标准方程
*
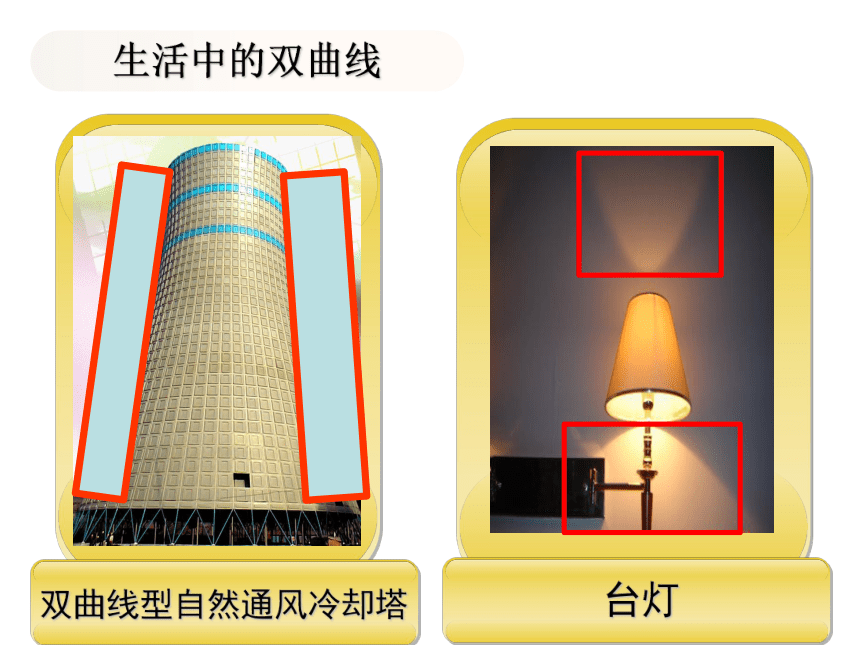
台灯
生活中的双曲线
双曲线型自然通风冷却塔
生活中的双曲线
生活感知
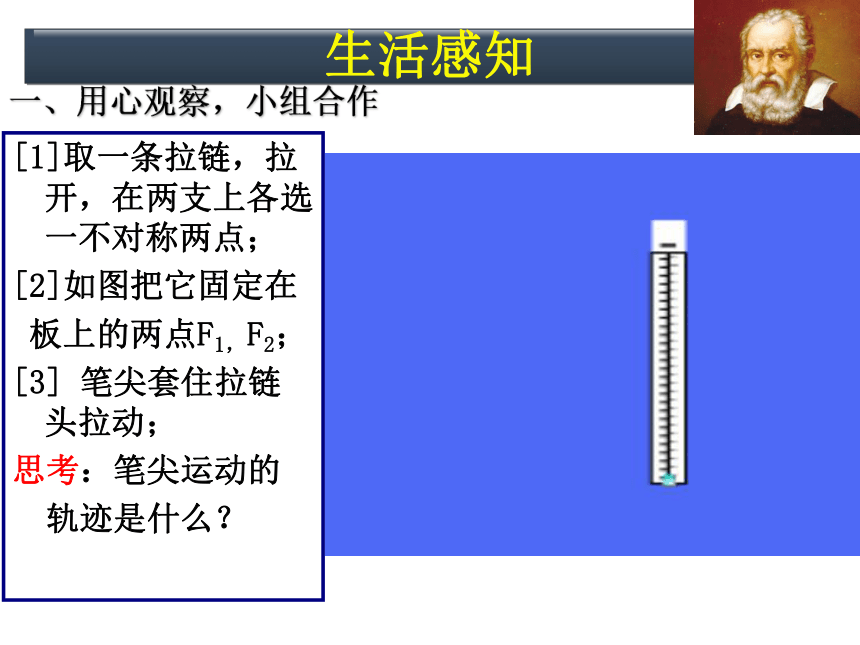
一、用心观察,小组合作
[1]取一条拉链,拉开,在两支上各选一不对称两点;
[2]如图把它固定在
板上的两点F1,F2;
[3] 笔尖套住拉链头拉动;
思考:笔尖运动的
轨迹是什么?
生活感知
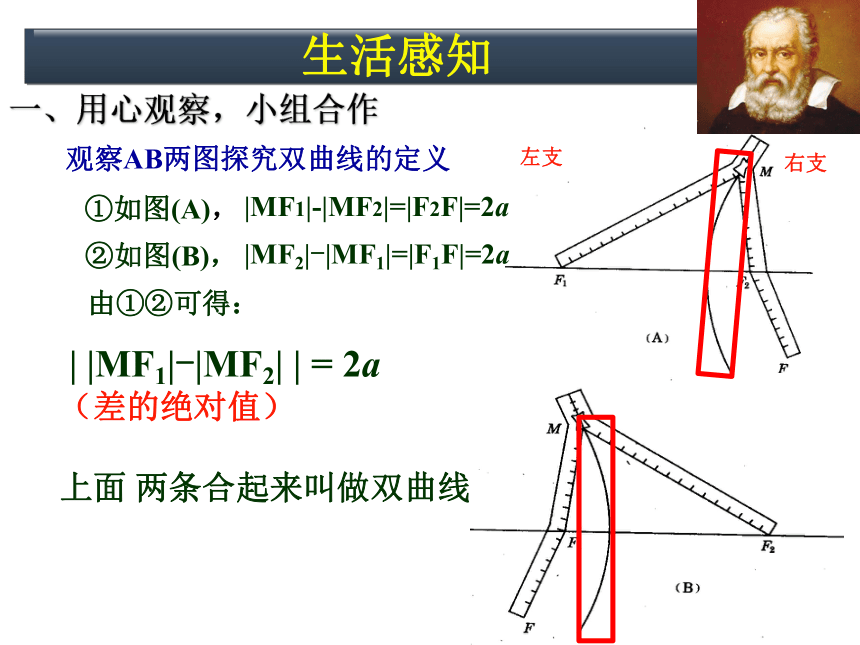
观察AB两图探究双曲线的定义
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B),
|MF2|-|MF1|=|F1F|=2a
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
上面 两条合起来叫做双曲线
一、用心观察,小组合作
右支
左支
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|,且不等于0)的点的轨迹叫做双曲线。
定点F1,F2叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距。
双曲线的定义
归纳:上面两条曲线合起来叫做双曲线,每一支叫做双曲线的一支,其中右支满足│MF1│>│MF2│,左支满足│MF1│<│MF2│
通常情况下,我们把|F1F2|记为2c(c>0); 常数记为2a(a>0).
问题5:定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
问题4:定义中为什么强调距离差的绝对值为常数?
若去掉绝对值,则为双曲线的一支
①若2a=2c,则轨迹是什么?
②若2a>2c,则轨迹是什么?
③若2a=0,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
F1
F2
F1
F2
分3种情况来看:
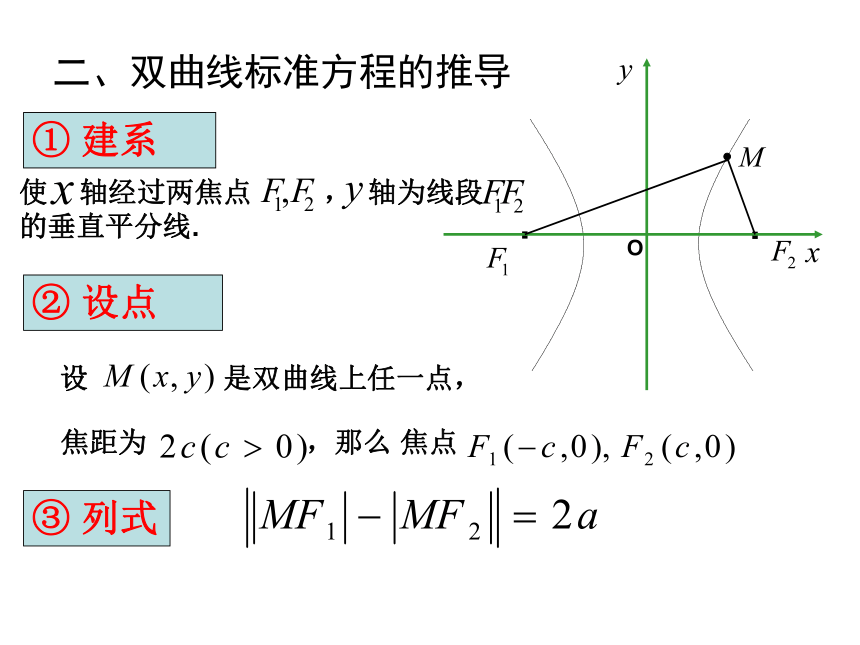
二、双曲线标准方程的推导
① 建系
使 轴经过两焦点 , 轴为线段 的垂直平分线.
O
② 设点
设 是双曲线上任一点,
焦距为 ,那么 焦点
③ 列式
将上述方程化为:
移项两边平方后整理得:
两边再平方后整理得:
由双曲线定义知:
即:
设
代入上式整理得:
两边同时除以 得:
④化简
这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在x轴上,焦点是 F1(-c,0),F2(c,0).
其中c2=a2+b2.
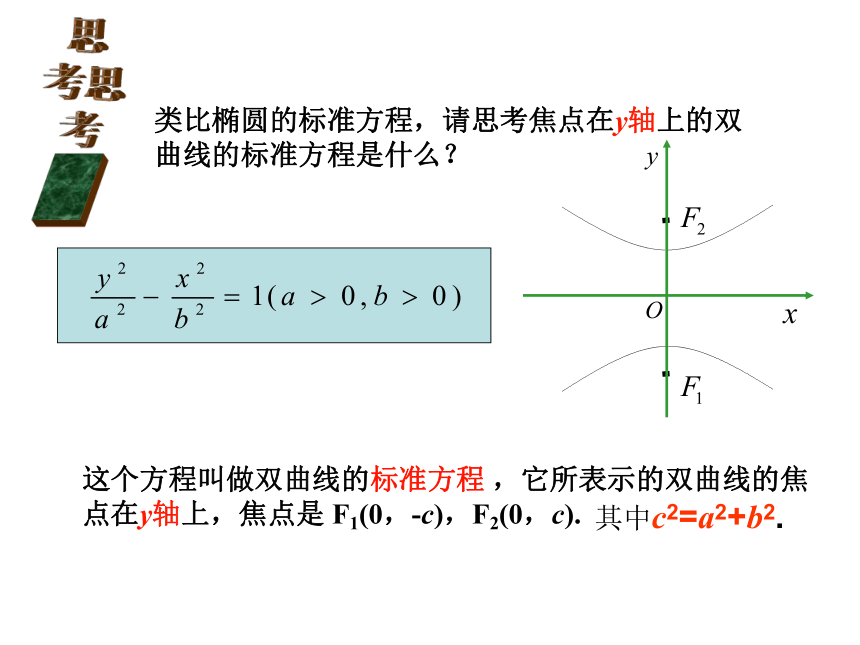
类比椭圆的标准方程,请思考焦点在y轴上的双曲线的标准方程是什么?
其中c2=a2+b2.
这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在y轴上,焦点是 F1(0,-c),F2(0,c).
三.双曲线两种标准方程
如果 的系数是正的,则焦点在 轴上;如果 的系数是正的,则焦点在 轴上。
O
M
F2
F1
x
y
F
2
F
1
M
x
O
y
焦点在y轴上的双曲线的标准方程
想一想
焦点在y轴上的双曲线的图象是什么?标准方程怎样求?
找出图形中a,b,c所表示的几何意义
观察图形
F1
F2
x
O
y
c
a
F2
F1
定义
图形
方程
焦点
a.b.c的关系
焦点位置的判定
||MF1|—|MF2||=2a(2a<|F1F2|)
F1(-c,0), F2(c,0)
F1(0,-c), F2(0,c)
c2=a2+b2
看x2,y2项系数的正负,哪项系数为正,焦点就在哪一条轴上
注:任何一条双曲线,只需选择适当的坐标系,其方程均可写成标准形式,当且仅当双曲线的焦点在坐标轴上,且两焦点的中点是原点时,其方程才具有标准形式
焦点位置确定:
椭圆看分母大小
双曲线看x2、y2
的系数正负
F2
F1
F2
F1
M
M
定 义
焦 点
a、b、c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
双曲线与椭圆之间的区别与联系:
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭圆
双曲线
F(0,±c)
F(0,±c)
口答:判断下列方程是否表示双曲线,若是,求出其焦点的坐标.
(1)
(2)
(3)
(4)
解:因为双曲线的焦点在x轴上,所以设它的标准方程为
因此,双曲线的标准方程为
求标准方程时,先定向,后定量.
例1、已知双曲线的焦点 F1(-5,0), F2(5,0),双曲线上一点P到焦点的距离差的绝对值等于6,求双曲线的标准方程。
所以2c=10,2a=8。即a=3,c=5
那么b2=c2-a2=25-9=16
根据已知条件,|F1F2|=10. ||PF1|-|PF2||=6,
图
变式训练
两条射线
轨迹不存在
1.若|PF1|-|PF2|=8呢?
2.若||PF1|-|PF2||=10呢?
3.若||PF1|-|PF2||=12呢?
例2、已知双曲线两个焦点的坐标为F1( - 5 , 0)、 F2(5 , 0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程。
解:因为双曲线的焦点在x轴上,所以设它的
∵ 2a =6 2c=10
∴ a =3 c =5
∴ b2= 52- 32= 16
∴ 所求双曲线的标准方程为
标准方程为
例3.求与椭圆 共焦点且过点 的双曲线的方程.
解:椭圆 的焦点为
可以设双曲线的方程为
又∵过点
则
∴
综上得
所以
思考题:已知双曲线上有两点P1、P2 ,坐标分别为(3,-4 ),
( ,5 ) ,求双曲线的标准方程。
1.分类法: 或 (a >0,b >0)
2.设 (m,n异号)
3.设 mx2+ny2=1 (m,n异号)
总结:和椭圆一样,求双曲线方程的基本方法是待定系数法,其基本步骤是:定类型,设方程,求系数.参数a、b是双曲线的定形条件,也是确定双曲线标准方程的两个独立条件.焦点F1、F2的位置是双曲线的定位条件,它决定着双曲线与坐标系的相对位置关系
方程Ax2+By2=c(c≠0)满足什么条件时表示双曲线 表示椭圆 还可以表示什么曲线
解:原方程化为:
A、焦点在x轴上的椭圆
C、焦点在y轴上的椭圆
B、焦点在y轴上的双曲线
D、焦点在x轴上的双曲线
∵ k>1
∴ k2-1> 0 1+k> 0
∴方程的曲线为焦点在y轴上的双曲线。
故 选(B)
例4:k > 1,则关于x、y的方程(1- k )x2+y2=k2- 1所表示的曲线是( )
使A、B两点在x轴上,并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
例5已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示,建立直角坐标系
x
y
o
P
B
A
图
即 2a=680,a=340
因此炮弹爆炸点的轨迹方程为
设爆炸点P的坐标为(x,y),则
例6.已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.
解:设动圆M与圆C1及圆C2分别外切于点A
和B,根据两圆外切的条件,
|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|
这表明动点M与两定点C2、C1的距离的差是常数2.根
据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2
的距离大,与C1的距离小),这里a=1,c=3,则b2=8,设点M
的坐标为(x,y),其轨迹方程为:
课堂练习
1、a=4,b=3 ,焦点在x轴上的双曲线的标准方程是
3、设双曲线 上的点P到(5,0)的距离是15,则P到
(-5,0)的距离是 .
7或23
4、如果方程 表示双曲线,则m的取值范围
是 __________
2、焦点为(0, -6),(0,6),经过点(2,-5)的双曲线的标 准方程是
m | m>-1或m< -2
5、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足|PF1| - |PF2|= 10,则P点的轨迹是( )
A、双曲线 B、双曲线一支
C、直线 D、一条射线
6、若椭圆 与双曲线 的焦点相同,则 a
=___________________
3
D
7、说明下列方程各表示什么曲线。
方程表示的曲线是双曲线
方程表示的曲线是双曲线的右支
方程表示的曲线是x轴上分别以F1和F2为端点,指向x轴的负半轴和
正半轴的两条射线。
8.已知定点A、B且 =4,动点P满足 , 则 的最小值是( )
9.若线段AB是过双曲线 左焦点F1的一条弦,且
F2为右焦点,则⊿ABF2的周长是_______________
4
(3)应用
(1)定义:
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
由方程定焦点:椭 圆看大小
双曲线看符号
3.2.1双曲线及其标准方程
*
台灯
生活中的双曲线
双曲线型自然通风冷却塔
生活中的双曲线
生活感知
一、用心观察,小组合作
[1]取一条拉链,拉开,在两支上各选一不对称两点;
[2]如图把它固定在
板上的两点F1,F2;
[3] 笔尖套住拉链头拉动;
思考:笔尖运动的
轨迹是什么?
生活感知
观察AB两图探究双曲线的定义
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B),
|MF2|-|MF1|=|F1F|=2a
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
上面 两条合起来叫做双曲线
一、用心观察,小组合作
右支
左支
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|,且不等于0)的点的轨迹叫做双曲线。
定点F1,F2叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距。
双曲线的定义
归纳:上面两条曲线合起来叫做双曲线,每一支叫做双曲线的一支,其中右支满足│MF1│>│MF2│,左支满足│MF1│<│MF2│
通常情况下,我们把|F1F2|记为2c(c>0); 常数记为2a(a>0).
问题5:定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
问题4:定义中为什么强调距离差的绝对值为常数?
若去掉绝对值,则为双曲线的一支
①若2a=2c,则轨迹是什么?
②若2a>2c,则轨迹是什么?
③若2a=0,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
F1
F2
F1
F2
分3种情况来看:
二、双曲线标准方程的推导
① 建系
使 轴经过两焦点 , 轴为线段 的垂直平分线.
O
② 设点
设 是双曲线上任一点,
焦距为 ,那么 焦点
③ 列式
将上述方程化为:
移项两边平方后整理得:
两边再平方后整理得:
由双曲线定义知:
即:
设
代入上式整理得:
两边同时除以 得:
④化简
这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在x轴上,焦点是 F1(-c,0),F2(c,0).
其中c2=a2+b2.
类比椭圆的标准方程,请思考焦点在y轴上的双曲线的标准方程是什么?
其中c2=a2+b2.
这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在y轴上,焦点是 F1(0,-c),F2(0,c).
三.双曲线两种标准方程
如果 的系数是正的,则焦点在 轴上;如果 的系数是正的,则焦点在 轴上。
O
M
F2
F1
x
y
F
2
F
1
M
x
O
y
焦点在y轴上的双曲线的标准方程
想一想
焦点在y轴上的双曲线的图象是什么?标准方程怎样求?
找出图形中a,b,c所表示的几何意义
观察图形
F1
F2
x
O
y
c
a
F2
F1
定义
图形
方程
焦点
a.b.c的关系
焦点位置的判定
||MF1|—|MF2||=2a(2a<|F1F2|)
F1(-c,0), F2(c,0)
F1(0,-c), F2(0,c)
c2=a2+b2
看x2,y2项系数的正负,哪项系数为正,焦点就在哪一条轴上
注:任何一条双曲线,只需选择适当的坐标系,其方程均可写成标准形式,当且仅当双曲线的焦点在坐标轴上,且两焦点的中点是原点时,其方程才具有标准形式
焦点位置确定:
椭圆看分母大小
双曲线看x2、y2
的系数正负
F2
F1
F2
F1
M
M
定 义
焦 点
a、b、c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
双曲线与椭圆之间的区别与联系:
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭圆
双曲线
F(0,±c)
F(0,±c)
口答:判断下列方程是否表示双曲线,若是,求出其焦点的坐标.
(1)
(2)
(3)
(4)
解:因为双曲线的焦点在x轴上,所以设它的标准方程为
因此,双曲线的标准方程为
求标准方程时,先定向,后定量.
例1、已知双曲线的焦点 F1(-5,0), F2(5,0),双曲线上一点P到焦点的距离差的绝对值等于6,求双曲线的标准方程。
所以2c=10,2a=8。即a=3,c=5
那么b2=c2-a2=25-9=16
根据已知条件,|F1F2|=10. ||PF1|-|PF2||=6,
图
变式训练
两条射线
轨迹不存在
1.若|PF1|-|PF2|=8呢?
2.若||PF1|-|PF2||=10呢?
3.若||PF1|-|PF2||=12呢?
例2、已知双曲线两个焦点的坐标为F1( - 5 , 0)、 F2(5 , 0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程。
解:因为双曲线的焦点在x轴上,所以设它的
∵ 2a =6 2c=10
∴ a =3 c =5
∴ b2= 52- 32= 16
∴ 所求双曲线的标准方程为
标准方程为
例3.求与椭圆 共焦点且过点 的双曲线的方程.
解:椭圆 的焦点为
可以设双曲线的方程为
又∵过点
则
∴
综上得
所以
思考题:已知双曲线上有两点P1、P2 ,坐标分别为(3,-4 ),
( ,5 ) ,求双曲线的标准方程。
1.分类法: 或 (a >0,b >0)
2.设 (m,n异号)
3.设 mx2+ny2=1 (m,n异号)
总结:和椭圆一样,求双曲线方程的基本方法是待定系数法,其基本步骤是:定类型,设方程,求系数.参数a、b是双曲线的定形条件,也是确定双曲线标准方程的两个独立条件.焦点F1、F2的位置是双曲线的定位条件,它决定着双曲线与坐标系的相对位置关系
方程Ax2+By2=c(c≠0)满足什么条件时表示双曲线 表示椭圆 还可以表示什么曲线
解:原方程化为:
A、焦点在x轴上的椭圆
C、焦点在y轴上的椭圆
B、焦点在y轴上的双曲线
D、焦点在x轴上的双曲线
∵ k>1
∴ k2-1> 0 1+k> 0
∴方程的曲线为焦点在y轴上的双曲线。
故 选(B)
例4:k > 1,则关于x、y的方程(1- k )x2+y2=k2- 1所表示的曲线是( )
使A、B两点在x轴上,并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
例5已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示,建立直角坐标系
x
y
o
P
B
A
图
即 2a=680,a=340
因此炮弹爆炸点的轨迹方程为
设爆炸点P的坐标为(x,y),则
例6.已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.
解:设动圆M与圆C1及圆C2分别外切于点A
和B,根据两圆外切的条件,
|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|
这表明动点M与两定点C2、C1的距离的差是常数2.根
据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2
的距离大,与C1的距离小),这里a=1,c=3,则b2=8,设点M
的坐标为(x,y),其轨迹方程为:
课堂练习
1、a=4,b=3 ,焦点在x轴上的双曲线的标准方程是
3、设双曲线 上的点P到(5,0)的距离是15,则P到
(-5,0)的距离是 .
7或23
4、如果方程 表示双曲线,则m的取值范围
是 __________
2、焦点为(0, -6),(0,6),经过点(2,-5)的双曲线的标 准方程是
m | m>-1或m< -2
5、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足|PF1| - |PF2|= 10,则P点的轨迹是( )
A、双曲线 B、双曲线一支
C、直线 D、一条射线
6、若椭圆 与双曲线 的焦点相同,则 a
=___________________
3
D
7、说明下列方程各表示什么曲线。
方程表示的曲线是双曲线
方程表示的曲线是双曲线的右支
方程表示的曲线是x轴上分别以F1和F2为端点,指向x轴的负半轴和
正半轴的两条射线。
8.已知定点A、B且 =4,动点P满足 , 则 的最小值是( )
9.若线段AB是过双曲线 左焦点F1的一条弦,且
F2为右焦点,则⊿ABF2的周长是_______________
4
(3)应用
(1)定义:
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
由方程定焦点:椭 圆看大小
双曲线看符号
