14.2 勾股定理的应用(1)
图片预览

文档简介
14.2 勾股定理的应用(1)
教学目标
知识与技能:能运用勾股定理及逆定理解决简单的实际问题.
过程与方法:经历勾股定理的应用过程,熟练掌握其应用方法,明确应用的条件.
情感态度与价值观:培养合情推理能力,体会数形结合的思维方法,激发学习热情.
重点、难点、关键
重点:勾股定理及逆定理的应用.
难点:勾股定理的正确使用.
关键:在现实情境中捕抓直角三角形,确定好直角三角形之后,再应用勾股定理.
教学准备
教师准备:投影片、直尺、圆规.
学生准备:复习勾股定理及逆定理,自制课本图14.2.1图.
教学过程
一、创设情境
1.问题情境:如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一点蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?(的值取3)
(1)自制一个圆柱,尝试从A点到B点沿圆柱侧面画出几条线段,你认为哪条路线最短呢?图(a)所示.
(2)如图(b),将圆柱侧面剪开展成一个长方形,从A点到B点的最短路线是什么?你画对了吗?
(3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?
2.思路点拨:引导学生尝试着在自制的圆柱侧面上寻找最短路线,提醒学生将圆柱侧面展开成长方形,此时学生发现了“两点之间的所有连线中,线段最短”这个结论,较易解决问题.
教师活动:操作投影仪,启发、引导学生动手操作,通过感性认识来突破学生空间想像的难点.
学生活动:观察、拿出事先准备好的学具,边操作边讨论边理解,寻求解决问题的途径.
媒体使用:投影显示“问题情境”.
二、范例学习
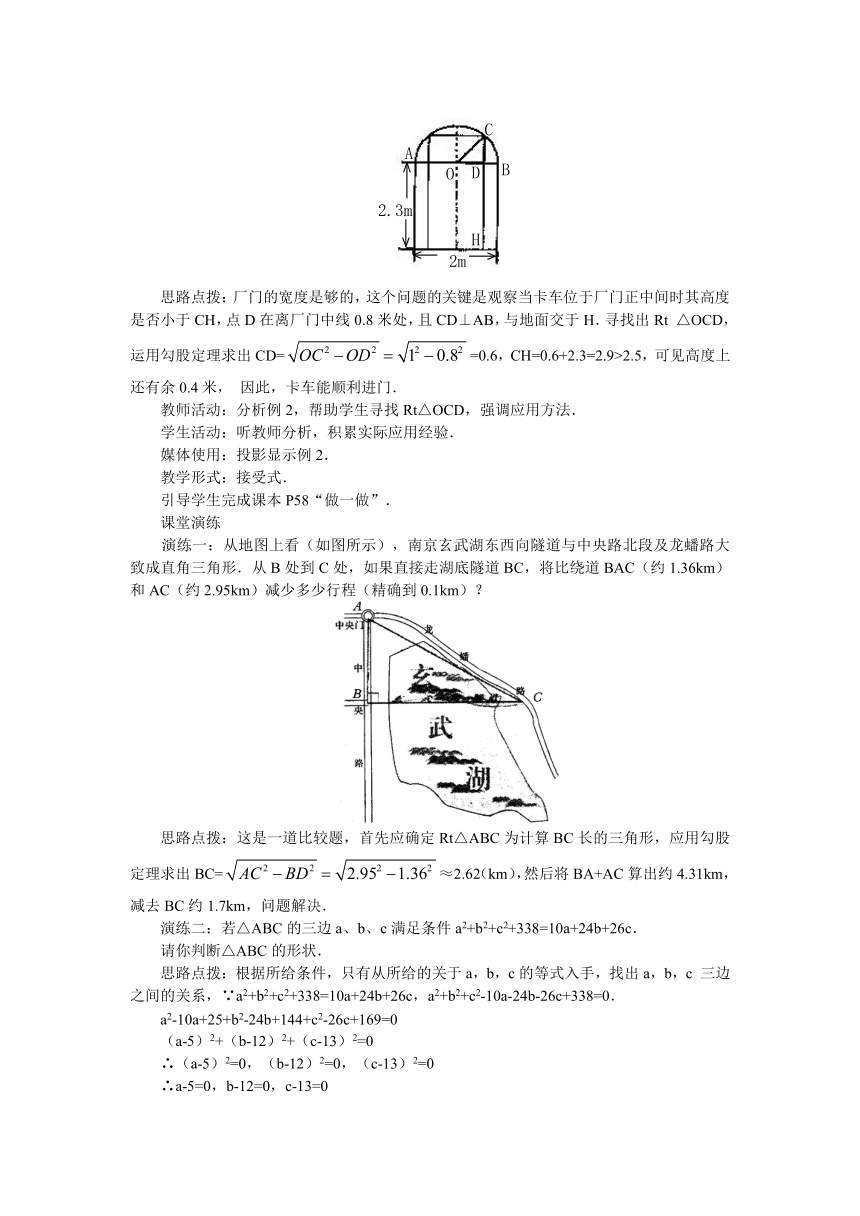
例2 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如课本P58图14.2.3的某工厂,问这辆卡车能否通过该工厂的厂门?
( http: / / )
思路点拨:厂门的宽度是够的,这个问题的关键是观察当卡车位于厂门正中间时其高度是否小于CH,点D在离厂门中线0.8米处,且CD⊥AB,与地面交于H.寻找出Rt△OCD,运用勾股定理求出CD==0.6,CH=0.6+2.3=2.9>2.5,可见高度上还有余0.4米,因此,卡车能顺利进门.
教师活动:分析例2,帮助学生寻找Rt△OCD,强调应用方法.
学生活动:听教师分析,积累实际应用经验.
媒体使用:投影显示例2.
教学形式:接受式.
引导学生完成课本P58“做一做”.
课堂演练
演练一:从地图上看(如图所示),南京玄武湖东西向隧道与中央路北段及龙蟠路大致成直角三角形.从B处到C处,如果直接走湖底隧道BC,将比绕道BAC(约1.36km)和AC(约2.95km)减少多少行程(精确到0.1km)?
思路点拨:这是一道比较题,首先应确定Rt△ABC为计算BC长的三角形,应用勾股定理求出BC= HYPERLINK "http://" ≈2.62(km),然后将BA+AC算出约4.31km,减去BC约1.7km,问题解决.
演练二:若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c.
请你判断△ABC的形状.
思路点拨:根据所给条件,只有从所给的关于a,b,c的等式入手,找出a,b,c三边之间的关系,∵a2+b2+c2+338=10a+24b+26c,a2+b2+c2-10a-24b-26c+338=0.
a2-10a+25+b2-24b+144+c2-26c+169=0
(a-5)2+(b-12)2+(c-13)2=0
∴(a-5)2=0,(b-12)2=0,(c-13)2=0
∴a-5=0,b-12=0,c-13=0
即a=5,b=12,c=13
∵a2+b2=52+122=132=c2
∴△ABC是直角三角形.
教师活动:操作投影仪,显示“课堂演练”,启发、引导学生.
学生活动:先独立完成,再有困难时,寻求同伴的帮助,通过交流,解决问题.
三、随堂练习
课本P58练习第1,2题.
2.探研时空.
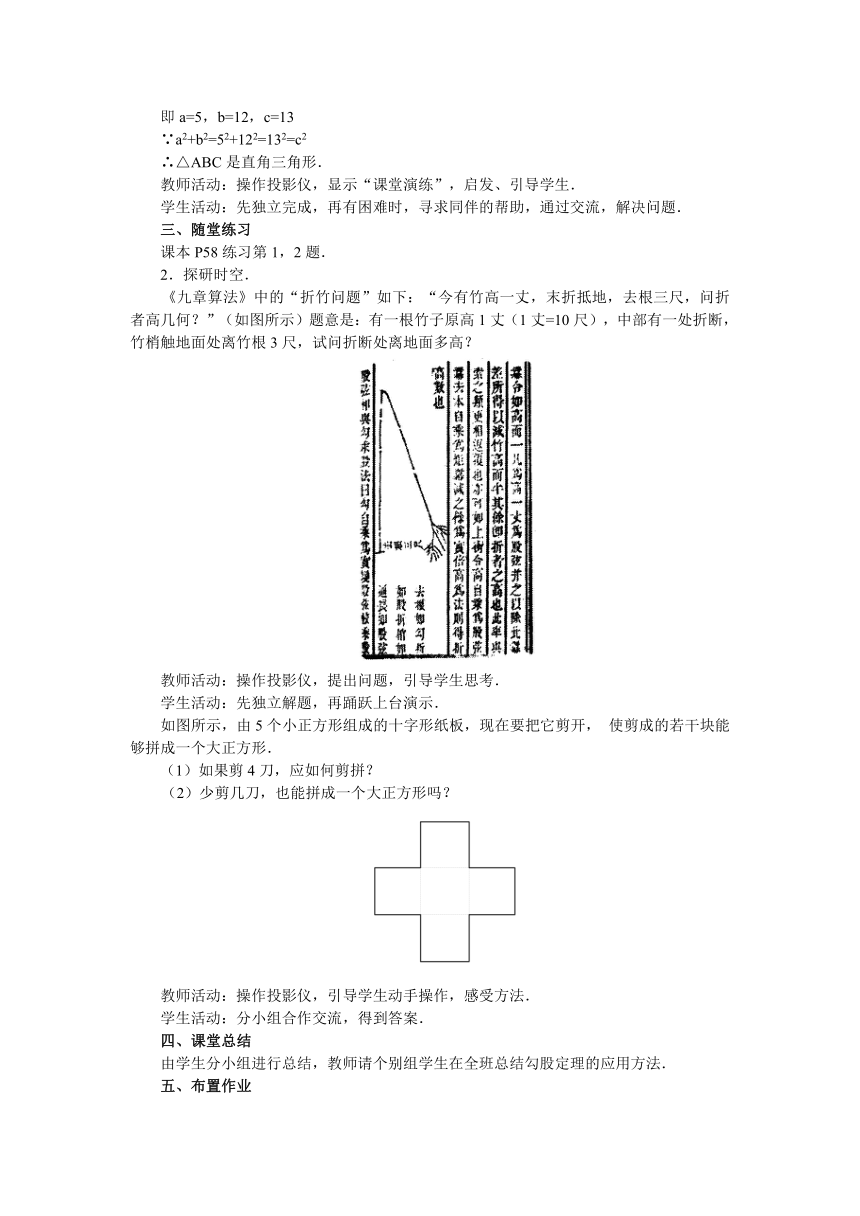
《九章算法》中的“折竹问题”如下:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”(如图所示)题意是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
教师活动:操作投影仪,提出问题,引导学生思考.
学生活动:先独立解题,再踊跃上台演示.
如图所示,由5个小正方形组成的十字形纸板,现在要把它剪开,使剪成的若干块能够拼成一个大正方形.
(1)如果剪4刀,应如何剪拼?
(2)少剪几刀,也能拼成一个大正方形吗?
( http: / / )
教师活动:操作投影仪,引导学生动手操作,感受方法.
学生活动:分小组合作交流,得到答案.
四、课堂总结
由学生分小组进行总结,教师请个别组学生在全班总结勾股定理的应用方法.
五、布置作业
1.课本P60习题14.2第1,2,3题.
2.选用课时作业设计.
六、课后反思(略)
第一课时作业设计
一、填空题
1.若一个三角形的一个角等于其他两个角的差,那么这个三角形是______三角形.
2.在△ABC中,∠A:∠B:∠C=1:2:3,则BC:AC:AB=________.
3.若△ABC中,a=12k,b=5k,c=13k(k>0),则△ABC为________三角形.
4.已知三角形的三条边长分别为41,40,9,则此三角形的面积为________.
5.△ABC的三边长分别是15,20,25,那么△ABC是_______三角形.
6.在△ABC中,AB=AC=4cm,∠A:∠B=2:5,过C点作△ABC的高CD,与AB交于D点,则CD=_______.
7.设直角三角形的三条边长为连续自然数,则这个直角三角形的面积是_____.
二、选择题
8.如图所示,正方形ABCD的边长为1cm,以对角线AC为边长再作一个正方形,则正方形ACEF的面积是( ).
A.2cm2 B.3cm2 C.5cm2 D.4cm2
9.如果梯子的底端建筑物有5m,15m长的梯子可达到该建筑物的高度大约是( ).
A.13m B.14m C.15m D.16m
10.以下各组数为边长,能组成直角三角形的是( ).
A.5,6,7 B.10,8,4 C.7,25,24 D.9,17,15
11.一个三角形的三边长分别为15,20,25,那么它的最长边上的高是( ).
A.12.5 B.12 C. D.9
12.以下列各组正数为边长,能组成直角三角形的是( ).
A.a-1,2a,a+1 B.a-1,2,a+1
D.a-1,a,a+1
13.以下列各组数为三边的三角形中,不是直角三角形的是( ).
A.,,2 B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
三、解答题
14.在△ABC中,AC=5,AB=12,BC=13,求BC边上的高AE的长.
15.如图所示,在△ABC中,∠C=90°,CD⊥AB垂足为D,BC=5cm,DC=4cm,求AC,AB的长.
( http: / / )
16.如图所示,点阵中以相邻4个点为顶点的小正方形面积为1,计算△ABC的周长和面积.(精确到0.1)
17.如图所示,是一个边长为a厘米的正方形,两条对角线AC与BD相交于O,观察此图,回答下面问题:
(1)线段AC的长是多少?
(2)图中有多少个直角三角形?
18.有一棵树较高(如图所示),无法直接量出它的高度,现给你一个能测仰角的仪器和一根皮尺,你能测出这棵树的高度吗?
( http: / / )
四、应用题
19.电工师傅把4米长的梯子靠在墙上,使梯脚离墙脚的距离为1.5米,准备在墙上安装电灯,当他爬上梯子后,发现高度不够,于是将梯子脚往墙脚移近0.5米(如图所示),那么,梯子顶端是否往上移动0.5米呢?
20.已知三边长分别为a,b,c的三角形是直角三角形,那么,三边长分别为a+1,b+1,c+1的三角形是否也是直角三角形呢?说明理由.
21.求下图(a~b)中字母所代表的正方形面积.
22.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6千米/时的速度向东行走1小时后乙出发,乙以5千米/时的速度向北行走,上午10:00,甲、乙两人相距多远?
23.在一块砖宽AN=5cm,长ND=10cm,CD上的点B距地面BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是多少?(如图14-2-12所示)
( http: / / )
答案:
一、1.直角 2.1::2 3.直角 4.360 5.直角 6.2cm 7.6
二、8.A 9.B 10.C 11.B 12.B 13.D
三、14. 16.动手操作
17.(1)a (2)有8个直角三角形
18.量出树顶一仰角为60°,则在Rt△ABC中,∠BAC=30°,
量出CB的距离,用勾股定理就能算出树的高度.
四、19.0.16米
梯子顶端A不是移动0.5米,因为在Rt△ABC中,AC=4,BC=1.5,
根据勾股定理,AB=≈3.71,
在Rt△A′BC′中,A′C′=4,BC′=1,
故A′B=≈3.87,从而A′A=3.87-3.71=0.16,
即梯子顶端A向上移动0.16米.
20.不会是直角三角形.
由题设知a2+b2-c2=0,∴(a+1)2+(b+1)2-(c+1)2=2(a+b-c)+1
而a+b>c,∴(a+1)2+(b+1)2≠(c+1)2.
21.625 22.13千米
23.17cm.
蚂蚁自A点出发,沿长方体表面爬到B处,要在曲面上找最短路径十分困难, 而在平面上找两点间的最短路径是较容易的,如图,AB长为A到B的最短距离.
在Rt△ABD中,AD=AN+ND=15,BD=8,
由勾股定理得AB2=AD2+BD2=289,所以AB=17.
因此,蚂蚁爬行的最短路径为17cm.
教学目标
知识与技能:能运用勾股定理及逆定理解决简单的实际问题.
过程与方法:经历勾股定理的应用过程,熟练掌握其应用方法,明确应用的条件.
情感态度与价值观:培养合情推理能力,体会数形结合的思维方法,激发学习热情.
重点、难点、关键
重点:勾股定理及逆定理的应用.
难点:勾股定理的正确使用.
关键:在现实情境中捕抓直角三角形,确定好直角三角形之后,再应用勾股定理.
教学准备
教师准备:投影片、直尺、圆规.
学生准备:复习勾股定理及逆定理,自制课本图14.2.1图.
教学过程
一、创设情境
1.问题情境:如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一点蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?(的值取3)
(1)自制一个圆柱,尝试从A点到B点沿圆柱侧面画出几条线段,你认为哪条路线最短呢?图(a)所示.
(2)如图(b),将圆柱侧面剪开展成一个长方形,从A点到B点的最短路线是什么?你画对了吗?
(3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?
2.思路点拨:引导学生尝试着在自制的圆柱侧面上寻找最短路线,提醒学生将圆柱侧面展开成长方形,此时学生发现了“两点之间的所有连线中,线段最短”这个结论,较易解决问题.
教师活动:操作投影仪,启发、引导学生动手操作,通过感性认识来突破学生空间想像的难点.
学生活动:观察、拿出事先准备好的学具,边操作边讨论边理解,寻求解决问题的途径.
媒体使用:投影显示“问题情境”.
二、范例学习
例2 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如课本P58图14.2.3的某工厂,问这辆卡车能否通过该工厂的厂门?
( http: / / )
思路点拨:厂门的宽度是够的,这个问题的关键是观察当卡车位于厂门正中间时其高度是否小于CH,点D在离厂门中线0.8米处,且CD⊥AB,与地面交于H.寻找出Rt△OCD,运用勾股定理求出CD==0.6,CH=0.6+2.3=2.9>2.5,可见高度上还有余0.4米,因此,卡车能顺利进门.
教师活动:分析例2,帮助学生寻找Rt△OCD,强调应用方法.
学生活动:听教师分析,积累实际应用经验.
媒体使用:投影显示例2.
教学形式:接受式.
引导学生完成课本P58“做一做”.
课堂演练
演练一:从地图上看(如图所示),南京玄武湖东西向隧道与中央路北段及龙蟠路大致成直角三角形.从B处到C处,如果直接走湖底隧道BC,将比绕道BAC(约1.36km)和AC(约2.95km)减少多少行程(精确到0.1km)?
思路点拨:这是一道比较题,首先应确定Rt△ABC为计算BC长的三角形,应用勾股定理求出BC= HYPERLINK "http://" ≈2.62(km),然后将BA+AC算出约4.31km,减去BC约1.7km,问题解决.
演练二:若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c.
请你判断△ABC的形状.
思路点拨:根据所给条件,只有从所给的关于a,b,c的等式入手,找出a,b,c三边之间的关系,∵a2+b2+c2+338=10a+24b+26c,a2+b2+c2-10a-24b-26c+338=0.
a2-10a+25+b2-24b+144+c2-26c+169=0
(a-5)2+(b-12)2+(c-13)2=0
∴(a-5)2=0,(b-12)2=0,(c-13)2=0
∴a-5=0,b-12=0,c-13=0
即a=5,b=12,c=13
∵a2+b2=52+122=132=c2
∴△ABC是直角三角形.
教师活动:操作投影仪,显示“课堂演练”,启发、引导学生.
学生活动:先独立完成,再有困难时,寻求同伴的帮助,通过交流,解决问题.
三、随堂练习
课本P58练习第1,2题.
2.探研时空.
《九章算法》中的“折竹问题”如下:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”(如图所示)题意是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
教师活动:操作投影仪,提出问题,引导学生思考.
学生活动:先独立解题,再踊跃上台演示.
如图所示,由5个小正方形组成的十字形纸板,现在要把它剪开,使剪成的若干块能够拼成一个大正方形.
(1)如果剪4刀,应如何剪拼?
(2)少剪几刀,也能拼成一个大正方形吗?
( http: / / )
教师活动:操作投影仪,引导学生动手操作,感受方法.
学生活动:分小组合作交流,得到答案.
四、课堂总结
由学生分小组进行总结,教师请个别组学生在全班总结勾股定理的应用方法.
五、布置作业
1.课本P60习题14.2第1,2,3题.
2.选用课时作业设计.
六、课后反思(略)
第一课时作业设计
一、填空题
1.若一个三角形的一个角等于其他两个角的差,那么这个三角形是______三角形.
2.在△ABC中,∠A:∠B:∠C=1:2:3,则BC:AC:AB=________.
3.若△ABC中,a=12k,b=5k,c=13k(k>0),则△ABC为________三角形.
4.已知三角形的三条边长分别为41,40,9,则此三角形的面积为________.
5.△ABC的三边长分别是15,20,25,那么△ABC是_______三角形.
6.在△ABC中,AB=AC=4cm,∠A:∠B=2:5,过C点作△ABC的高CD,与AB交于D点,则CD=_______.
7.设直角三角形的三条边长为连续自然数,则这个直角三角形的面积是_____.
二、选择题
8.如图所示,正方形ABCD的边长为1cm,以对角线AC为边长再作一个正方形,则正方形ACEF的面积是( ).
A.2cm2 B.3cm2 C.5cm2 D.4cm2
9.如果梯子的底端建筑物有5m,15m长的梯子可达到该建筑物的高度大约是( ).
A.13m B.14m C.15m D.16m
10.以下各组数为边长,能组成直角三角形的是( ).
A.5,6,7 B.10,8,4 C.7,25,24 D.9,17,15
11.一个三角形的三边长分别为15,20,25,那么它的最长边上的高是( ).
A.12.5 B.12 C. D.9
12.以下列各组正数为边长,能组成直角三角形的是( ).
A.a-1,2a,a+1 B.a-1,2,a+1
D.a-1,a,a+1
13.以下列各组数为三边的三角形中,不是直角三角形的是( ).
A.,,2 B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
三、解答题
14.在△ABC中,AC=5,AB=12,BC=13,求BC边上的高AE的长.
15.如图所示,在△ABC中,∠C=90°,CD⊥AB垂足为D,BC=5cm,DC=4cm,求AC,AB的长.
( http: / / )
16.如图所示,点阵中以相邻4个点为顶点的小正方形面积为1,计算△ABC的周长和面积.(精确到0.1)
17.如图所示,是一个边长为a厘米的正方形,两条对角线AC与BD相交于O,观察此图,回答下面问题:
(1)线段AC的长是多少?
(2)图中有多少个直角三角形?
18.有一棵树较高(如图所示),无法直接量出它的高度,现给你一个能测仰角的仪器和一根皮尺,你能测出这棵树的高度吗?
( http: / / )
四、应用题
19.电工师傅把4米长的梯子靠在墙上,使梯脚离墙脚的距离为1.5米,准备在墙上安装电灯,当他爬上梯子后,发现高度不够,于是将梯子脚往墙脚移近0.5米(如图所示),那么,梯子顶端是否往上移动0.5米呢?
20.已知三边长分别为a,b,c的三角形是直角三角形,那么,三边长分别为a+1,b+1,c+1的三角形是否也是直角三角形呢?说明理由.
21.求下图(a~b)中字母所代表的正方形面积.
22.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6千米/时的速度向东行走1小时后乙出发,乙以5千米/时的速度向北行走,上午10:00,甲、乙两人相距多远?
23.在一块砖宽AN=5cm,长ND=10cm,CD上的点B距地面BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是多少?(如图14-2-12所示)
( http: / / )
答案:
一、1.直角 2.1::2 3.直角 4.360 5.直角 6.2cm 7.6
二、8.A 9.B 10.C 11.B 12.B 13.D
三、14. 16.动手操作
17.(1)a (2)有8个直角三角形
18.量出树顶一仰角为60°,则在Rt△ABC中,∠BAC=30°,
量出CB的距离,用勾股定理就能算出树的高度.
四、19.0.16米
梯子顶端A不是移动0.5米,因为在Rt△ABC中,AC=4,BC=1.5,
根据勾股定理,AB=≈3.71,
在Rt△A′BC′中,A′C′=4,BC′=1,
故A′B=≈3.87,从而A′A=3.87-3.71=0.16,
即梯子顶端A向上移动0.16米.
20.不会是直角三角形.
由题设知a2+b2-c2=0,∴(a+1)2+(b+1)2-(c+1)2=2(a+b-c)+1
而a+b>c,∴(a+1)2+(b+1)2≠(c+1)2.
21.625 22.13千米
23.17cm.
蚂蚁自A点出发,沿长方体表面爬到B处,要在曲面上找最短路径十分困难, 而在平面上找两点间的最短路径是较容易的,如图,AB长为A到B的最短距离.
在Rt△ABD中,AD=AN+ND=15,BD=8,
由勾股定理得AB2=AD2+BD2=289,所以AB=17.
因此,蚂蚁爬行的最短路径为17cm.
