2021-2022学年人教版数学九年级上册22.3实际问题与二次函数课时提升卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册22.3实际问题与二次函数课时提升卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 729.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 09:19:42 | ||
图片预览

文档简介
22.3实际问题与二次函数课时提升卷—2021-2022学年人教版数学九年级上册
一、单选题
1.如图所示,将一根长m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系 B.一次函数关系 C.二次函数关系 D.反比例函数关系
2.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A. B. C. D.
3.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,若第二个月的增长率是,第三个月的增长率是第二个月的两倍,那么与的函数关系是 ( )
A. B.
C. D.
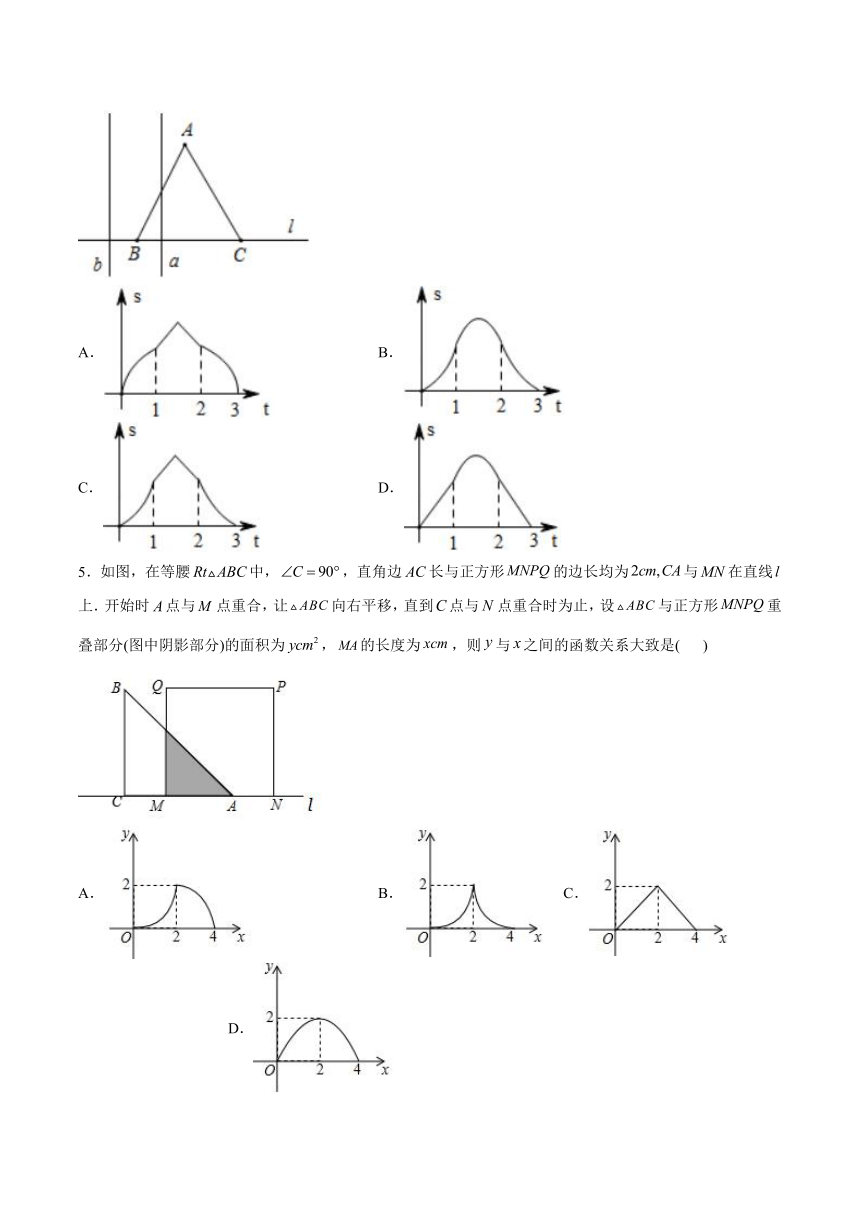
4.如图,边长为的正的边在直线上,两条距离为的平行直线和垂直于直线,和同时向右移动(的起始位置在点),速度均为每秒个单位,运动时间为(秒),直到到达点停止,在和向右移动的过程中,记夹在和间的部分的面积为,则关于的函数图象大致为( )
A. B.
C. D.
5.如图,在等腰中,,直角边长与正方形的边长均为与在直线上.开始时点与点重合,让向右平移,直到点与点重合时为止,设与正方形重叠部分(图中阴影部分)的面积为,的长度为,则与之间的函数关系大致是( )
A. B. C. D.
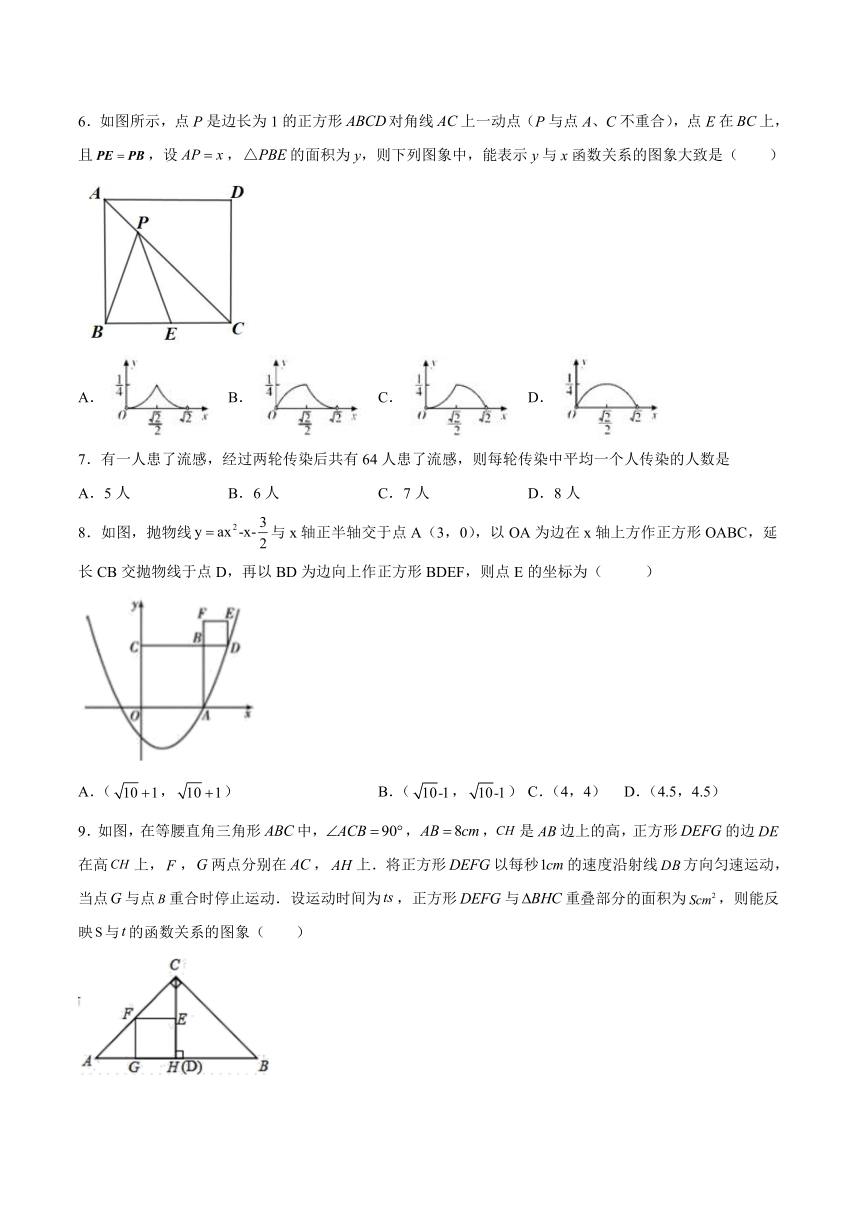
6.如图所示,点P是边长为1的正方形对角线上一动点(P与点A、C不重合),点E在上,且,设,的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
A. B. C. D.
7.有一人患了流感,经过两轮传染后共有64人患了流感,则每轮传染中平均一个人传染的人数是
A.5人 B.6人 C.7人 D.8人
8.如图,抛物线与x轴正半轴交于点A(3,0),以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则点E的坐标为( )
A.(,) B.(,) C.(4,4) D.(4.5,4.5)
9.如图,在等腰直角三角形中,,,是边上的高,正方形的边在高上,,两点分别在,上.将正方形以每秒的速度沿射线方向匀速运动,当点与点重合时停止运动.设运动时间为,正方形与重叠部分的面积为,则能反映与的函数关系的图象( )
A. B. C. D.
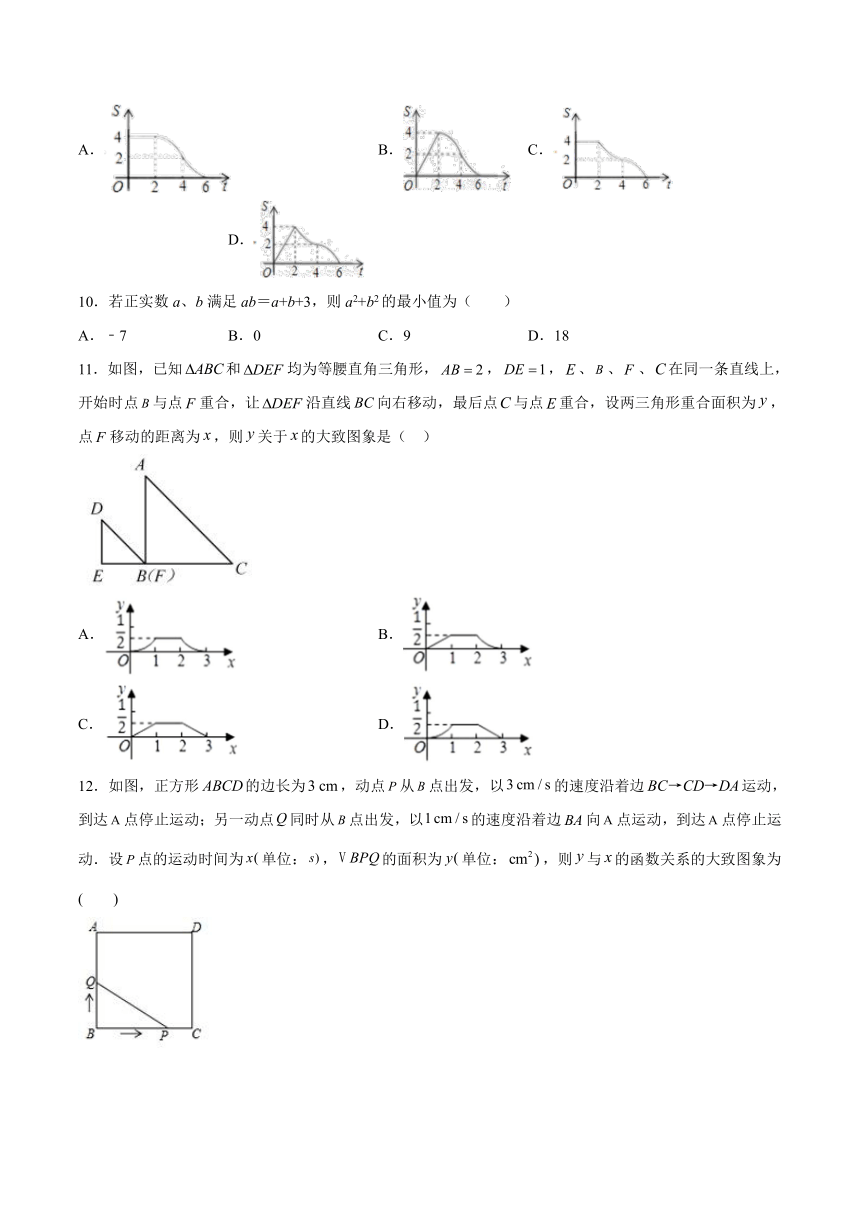
10.若正实数a、b满足ab=a+b+3,则a2+b2的最小值为( )
A.﹣7 B.0 C.9 D.18
11.如图,已知和均为等腰直角三角形,,,、、、在同一条直线上,开始时点与点重合,让沿直线向右移动,最后点与点重合,设两三角形重合面积为,点移动的距离为,则关于的大致图象是( )
A. B.
C. D.
12.如图,正方形的边长为,动点从点出发,以的速度沿着边运动,到达点停止运动;另一动点同时从点出发,以的速度沿着边向点运动,到达点停止运动.设点的运动时间为单位:,的面积为单位:,则与的函数关系的大致图象为( )
A. B. C. D.
二、填空题
13.一个涵洞成抛物线形,它的截面如图,当水面宽AB=1.6米时,涵洞顶点与水面的距离为2.4m.涵洞所在抛物线的解析式是_____________.
14.在某市治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为8m的正方形ABCD,改建的绿地为矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG=2BE.那么当BE=_____m时,绿地AEFG的面积最大.
15.用一段长为的篱笆围成一个一边靠墙的矩形养鸡场,若墙长,则这个养鸡场最大面积为______.
16.如图,在直角三角形中,,是边上一点,以为边,在上方作等腰直角三角形,使得,连接.若,,则的最小值是_______.
17.已知点P为二次函数y=x2﹣2x﹣3图象上一点,设这个二次函数的图象与x轴交于A,B两点(A在B的右侧),与y轴交于C点,若△APC为直角三角形且AC为直角边,则点P的横坐标的值为_____.
三、解答题
18.如图,在平面直角坐标系中.抛物线L:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点A的坐标为(﹣4,0),抛物线的对称轴是直线x=﹣3.且经过A、C两点的直线为y=kx+4.
(1)求抛物线L的函数表达式;
(2)若将抛物线L沿x轴翻折,得到新抛物线L′,抛物线L′上是否存在一点P使得SAOP=SABC,若存在,请求出点P的坐标;若不存在,请说明理由.
19.我区绿色和特色农产品在市场上颇具竞争力.外贸商经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据经理提供的预测信息、(如右图)帮经理解决以下问题:
1.蘑菇的市场价格每天每千克上涨0.1元; 2.平均每天有10千克的蘑菇损坏不能出售; 3.冷库存放这批蘑菇时每天需要支出各种费用合计240元; 4.蘑菇在冷库中最多保存110天.
(1)若经理想将这批蘑菇存放x天后一次性出售,则x天后这批蘑菇的销售单价为________元,这批蘑菇的销售量是___________千克;
(2)经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为10万元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
20.下图是某同学正在设计的一动画示意图,轴上依次有,,三个点,且,在上方有五个台阶(各拐角均为),每个台阶的高、宽分别是1和1.5,台阶到轴距离.从点处向右上方沿抛物线:发出一个带光的点.
(1)求点的横坐标,且在图中补画出轴,并直接指出点会落在哪个台阶上;
(2)当点落到台阶上后立即弹起,又形成了另一条与形状相同的抛物线,且最大高度为11,求的解析式,并说明其对称轴是否与台阶有交点;
(3)在轴上从左到右有两点,,且,从点向上作轴,且.在沿轴左右平移时,必须保证(2)中沿抛物线下落的点能落在边(包括端点)上,则点横坐标的最大值比最小值大多少?
(注:(2)中不必写的取值范围)
21.如图,已知二次函数的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求该二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为点Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点P,使PMC为等腰三角形?如果存在,求出点P的坐标;如果不存在,请说明理由.
参考答案
1.C
2.A
3.A
4.B
5.A
6.D
7.C
8.A
9.B
10.D
11.A
12.A
13.
14.2
15.64
16.
17.﹣1或﹣2
18.(1)y=x2+3x+4;(2)存在,点P的坐标为(﹣3,)或(﹣3,﹣)或(﹣3﹣,﹣)
19.(1);;(2)100天;(3)存放110天后出售这批香菇可获得最大利润16500元
20.(1),见解析,点会落在的台阶上;(2),其对称轴与台阶有交点;(3).
21.(1);(2)S四边形ACPQ;(3)存在,,,
一、单选题
1.如图所示,将一根长m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系 B.一次函数关系 C.二次函数关系 D.反比例函数关系
2.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A. B. C. D.
3.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,若第二个月的增长率是,第三个月的增长率是第二个月的两倍,那么与的函数关系是 ( )
A. B.
C. D.
4.如图,边长为的正的边在直线上,两条距离为的平行直线和垂直于直线,和同时向右移动(的起始位置在点),速度均为每秒个单位,运动时间为(秒),直到到达点停止,在和向右移动的过程中,记夹在和间的部分的面积为,则关于的函数图象大致为( )
A. B.
C. D.
5.如图,在等腰中,,直角边长与正方形的边长均为与在直线上.开始时点与点重合,让向右平移,直到点与点重合时为止,设与正方形重叠部分(图中阴影部分)的面积为,的长度为,则与之间的函数关系大致是( )
A. B. C. D.
6.如图所示,点P是边长为1的正方形对角线上一动点(P与点A、C不重合),点E在上,且,设,的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
A. B. C. D.
7.有一人患了流感,经过两轮传染后共有64人患了流感,则每轮传染中平均一个人传染的人数是
A.5人 B.6人 C.7人 D.8人
8.如图,抛物线与x轴正半轴交于点A(3,0),以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则点E的坐标为( )
A.(,) B.(,) C.(4,4) D.(4.5,4.5)
9.如图,在等腰直角三角形中,,,是边上的高,正方形的边在高上,,两点分别在,上.将正方形以每秒的速度沿射线方向匀速运动,当点与点重合时停止运动.设运动时间为,正方形与重叠部分的面积为,则能反映与的函数关系的图象( )
A. B. C. D.
10.若正实数a、b满足ab=a+b+3,则a2+b2的最小值为( )
A.﹣7 B.0 C.9 D.18
11.如图,已知和均为等腰直角三角形,,,、、、在同一条直线上,开始时点与点重合,让沿直线向右移动,最后点与点重合,设两三角形重合面积为,点移动的距离为,则关于的大致图象是( )
A. B.
C. D.
12.如图,正方形的边长为,动点从点出发,以的速度沿着边运动,到达点停止运动;另一动点同时从点出发,以的速度沿着边向点运动,到达点停止运动.设点的运动时间为单位:,的面积为单位:,则与的函数关系的大致图象为( )
A. B. C. D.
二、填空题
13.一个涵洞成抛物线形,它的截面如图,当水面宽AB=1.6米时,涵洞顶点与水面的距离为2.4m.涵洞所在抛物线的解析式是_____________.
14.在某市治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为8m的正方形ABCD,改建的绿地为矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG=2BE.那么当BE=_____m时,绿地AEFG的面积最大.
15.用一段长为的篱笆围成一个一边靠墙的矩形养鸡场,若墙长,则这个养鸡场最大面积为______.
16.如图,在直角三角形中,,是边上一点,以为边,在上方作等腰直角三角形,使得,连接.若,,则的最小值是_______.
17.已知点P为二次函数y=x2﹣2x﹣3图象上一点,设这个二次函数的图象与x轴交于A,B两点(A在B的右侧),与y轴交于C点,若△APC为直角三角形且AC为直角边,则点P的横坐标的值为_____.
三、解答题
18.如图,在平面直角坐标系中.抛物线L:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点A的坐标为(﹣4,0),抛物线的对称轴是直线x=﹣3.且经过A、C两点的直线为y=kx+4.
(1)求抛物线L的函数表达式;
(2)若将抛物线L沿x轴翻折,得到新抛物线L′,抛物线L′上是否存在一点P使得SAOP=SABC,若存在,请求出点P的坐标;若不存在,请说明理由.
19.我区绿色和特色农产品在市场上颇具竞争力.外贸商经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据经理提供的预测信息、(如右图)帮经理解决以下问题:
1.蘑菇的市场价格每天每千克上涨0.1元; 2.平均每天有10千克的蘑菇损坏不能出售; 3.冷库存放这批蘑菇时每天需要支出各种费用合计240元; 4.蘑菇在冷库中最多保存110天.
(1)若经理想将这批蘑菇存放x天后一次性出售,则x天后这批蘑菇的销售单价为________元,这批蘑菇的销售量是___________千克;
(2)经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为10万元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
20.下图是某同学正在设计的一动画示意图,轴上依次有,,三个点,且,在上方有五个台阶(各拐角均为),每个台阶的高、宽分别是1和1.5,台阶到轴距离.从点处向右上方沿抛物线:发出一个带光的点.
(1)求点的横坐标,且在图中补画出轴,并直接指出点会落在哪个台阶上;
(2)当点落到台阶上后立即弹起,又形成了另一条与形状相同的抛物线,且最大高度为11,求的解析式,并说明其对称轴是否与台阶有交点;
(3)在轴上从左到右有两点,,且,从点向上作轴,且.在沿轴左右平移时,必须保证(2)中沿抛物线下落的点能落在边(包括端点)上,则点横坐标的最大值比最小值大多少?
(注:(2)中不必写的取值范围)
21.如图,已知二次函数的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求该二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为点Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点P,使PMC为等腰三角形?如果存在,求出点P的坐标;如果不存在,请说明理由.
参考答案
1.C
2.A
3.A
4.B
5.A
6.D
7.C
8.A
9.B
10.D
11.A
12.A
13.
14.2
15.64
16.
17.﹣1或﹣2
18.(1)y=x2+3x+4;(2)存在,点P的坐标为(﹣3,)或(﹣3,﹣)或(﹣3﹣,﹣)
19.(1);;(2)100天;(3)存放110天后出售这批香菇可获得最大利润16500元
20.(1),见解析,点会落在的台阶上;(2),其对称轴与台阶有交点;(3).
21.(1);(2)S四边形ACPQ;(3)存在,,,
同课章节目录
