数学七年级下人教新课标5.1.1相交线
文档属性
| 名称 | 数学七年级下人教新课标5.1.1相交线 |  | |
| 格式 | zip | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-13 13:02:04 | ||
图片预览



文档简介
(共19张PPT)
人教版七年级下册第五章:相交线与平行线
5.1.1课题:相交线
授 课 流 程:
【评价与反思】
【学习目标及重难点】
【学生展示】
【学生达标测试】
【知识链接】
【合作探究一】
【合作探究二】
5.1.1 相交线
第五章 相交线
了解邻补角和对顶角的概念,领会邻补角和对顶角的性质。
能在具体的情境或图形中找出相交线和平行线。
从对顶角的性质的推理中初步了解数学推理方法步骤。
进一步形成积极参与数学活动、与他人合作交流意识,激发学习空间与图形的兴趣。
重点 :邻补角、对顶角的概念,对顶角性质与应用.
难点:理解对顶角相等的性质的探索及几何说理和表达能力的培养。
学习目标:
重点与难点:
返回
欣赏下面的彩图,找出图中的相交线,你能举出生活中的相交线的例子吗?
举例: 如:剪刀。________________________________
知识链接:
返回
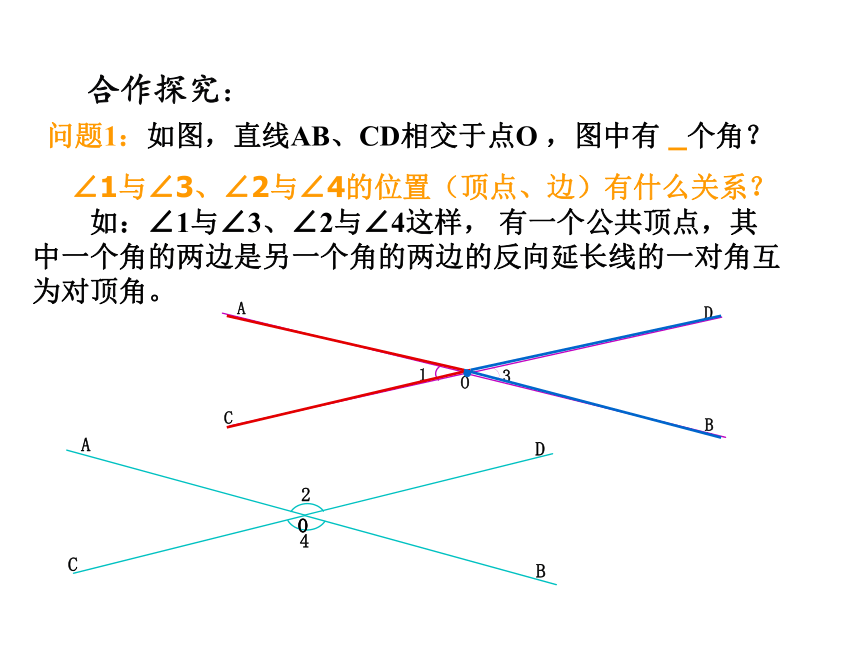
问题1:如图,直线AB、CD相交于点O ,图中有 _个角?
∠1与∠3、∠2与∠4的位置(顶点、边)有什么关系?
如:∠1与∠3、∠2与∠4这样, 有一个公共顶点,其中一个角的两边是另一个角的两边的反向延长线的一对角互为对顶角。
合作探究:
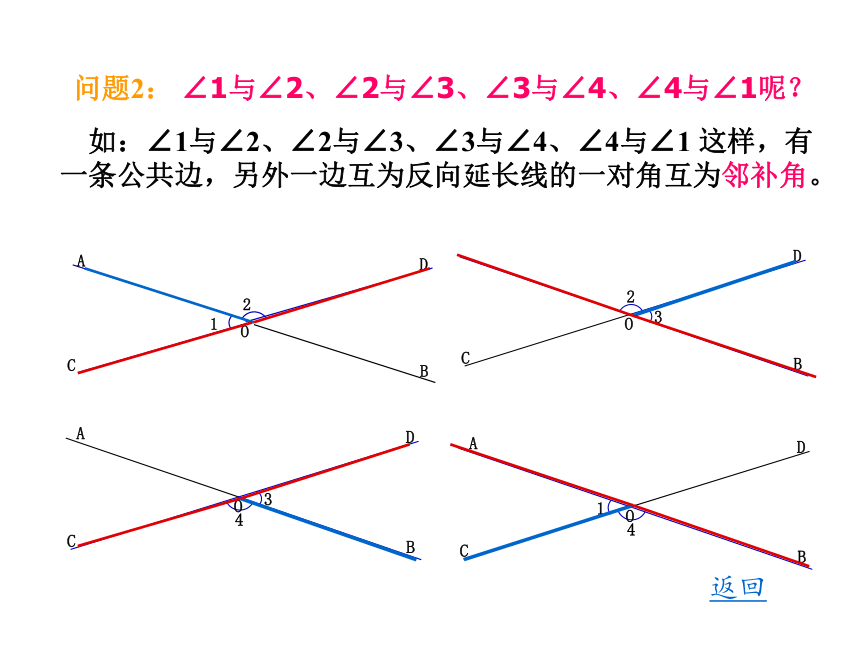
问题2: ∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1呢?
如:∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1 这样,有一条公共边,另外一边互为反向延长线的一对角互为邻补角。
O
B
2
1
C
A
D
返回
对顶角:
邻补角:
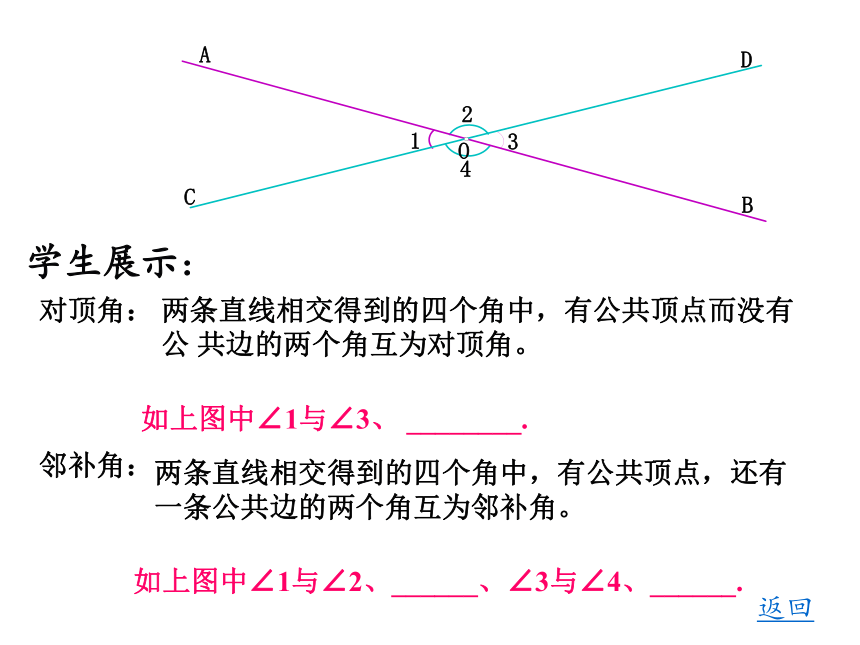
学生展示:
如上图中∠1与∠3、 ________.
如上图中∠1与∠2、______、∠3与∠4、______.
返回
两条直线相交得到的四个角中,有公共顶点而没有公 共边的两个角互为对顶角。
两条直线相交得到的四个角中,有公共顶点,还有一条公共边的两个角互为邻补角。
问题3:邻补角一定互为补角。对顶角又有什么样的大小关系呢?
3
2
1
我们可以做下面的推理:
∵∠1与∠2互补,
∠2与∠3互补(邻补角定义),
∴∠1=∠3(同角的补角相等).
同理,∠2=∠4 .
对顶角相等
D
C
B
A
例题探讨: 如图,射线OC交直线AB于点O,图中共有几个角?它们是邻补角还是对顶角? 为什么?
C
A
B
O
拓展: 邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角。
解:图中共有两个角,它们互为邻补角。因为它们有一个公共边,另一边互为反向延长线。
返回
学生达标一
1、下列各图中,O、P在直线AB上,图中有邻补角吗?有对顶角吗?如果有,请把它们指出来。
无对顶角,有两对邻补角:
∠AOC与∠BOC, ____________
无对顶角,有两对邻补角:
________,∠APD与∠BPD
无对顶角,有三 对邻补角:
__________,∠AOD与∠BOD
∠AOE与∠BOE
无对顶角,有三 对邻补角:
∠AOE与∠BOE, ___________,
∠AOD与∠BOD
A
C
A
B
D
O
(1)
B
C
D
O
P
(2)
C
A
B
D
O
E
(4)
A
B
C
D
O
E
(3)
2、如图,已知直线AE、BD相交于点C.
(1)图中哪些角是对顶角?
A
C
D
E
B
答:邻补角有四对:
∠ACB与∠ACD、∠ACB与∠BCE、
∠DCE与∠ACD、∠DCE与∠BCE.
答:对顶角有两对:
∠ACB与∠DCE、∠ACD与∠BCE.
(2)哪些角是邻补角?
3.如图,AB、CD、EF是经过点O的三条直线,说出:
∠AOC 的对顶角 , ∠FOB 的对顶角 , ∠DOF 的对顶角 , ∠AOD 的对顶角 , ∠EOB 的对顶角 ,∠AOF 的邻补角 、
A
B
C
E
F
D
O
是∠BOD
是∠AOE
是∠COE
是∠BOC
是∠AOF
是∠BOF 和∠AOE
4、下列图形中,∠1和∠2是对顶角的图形是( )
1
1
1
1
2
2
2
2
(A)
(B)
(C)
(D)
C
5、下列说法是否正确?为什么?
(1)有公共顶点的两个角是对顶角。
答:不正确。如图,∠AOB与∠COD有
公共顶点O,但它们不是对顶角。
A
O
C
D
B
(2)有公共顶点而没有公共边的两个角是对顶角。
答:不正确。如上图,∠AOB与∠COD有公共顶点O,而且
没有公共边,但它们不是对顶角。
(3)相邻的两个角是邻补角。
答:不正确。如图,∠AOB 与∠BOC 有
公共顶点和一条公共边,是相邻的两
个角,但不互补,所以不是邻补角。
A
C
B
O
1、 对顶角相等。反过来, 相等的 两个角一定是对顶角吗?
2
3
4
2、邻补角互补。反过来,互补的角(度数的和等于180°的两个角)一定是邻补角吗?
学生达标二
返回
课堂评价与反思:
小结: 今天,我们学习了两直线相交的有关知识,弄清对顶角和邻补角这两个重要概念以及“对顶角相等”这一重要性质,因为它们在我们今后的学习中经常用到;要学会从复杂的图形中分解出基本的图形,从而正确识别对顶角、邻补角,逐步训练和提高自己的识图能力和计算推理能力。
评价:第一组:__分 第二组: __分 第三组: __分
第四组: __分 第五组: __分 第六组: __分
反思:
返回
返回知识链接
返回授课流程
人教版七年级下册第五章:相交线与平行线
5.1.1课题:相交线
授 课 流 程:
【评价与反思】
【学习目标及重难点】
【学生展示】
【学生达标测试】
【知识链接】
【合作探究一】
【合作探究二】
5.1.1 相交线
第五章 相交线
了解邻补角和对顶角的概念,领会邻补角和对顶角的性质。
能在具体的情境或图形中找出相交线和平行线。
从对顶角的性质的推理中初步了解数学推理方法步骤。
进一步形成积极参与数学活动、与他人合作交流意识,激发学习空间与图形的兴趣。
重点 :邻补角、对顶角的概念,对顶角性质与应用.
难点:理解对顶角相等的性质的探索及几何说理和表达能力的培养。
学习目标:
重点与难点:
返回
欣赏下面的彩图,找出图中的相交线,你能举出生活中的相交线的例子吗?
举例: 如:剪刀。________________________________
知识链接:
返回
问题1:如图,直线AB、CD相交于点O ,图中有 _个角?
∠1与∠3、∠2与∠4的位置(顶点、边)有什么关系?
如:∠1与∠3、∠2与∠4这样, 有一个公共顶点,其中一个角的两边是另一个角的两边的反向延长线的一对角互为对顶角。
合作探究:
问题2: ∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1呢?
如:∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1 这样,有一条公共边,另外一边互为反向延长线的一对角互为邻补角。
O
B
2
1
C
A
D
返回
对顶角:
邻补角:
学生展示:
如上图中∠1与∠3、 ________.
如上图中∠1与∠2、______、∠3与∠4、______.
返回
两条直线相交得到的四个角中,有公共顶点而没有公 共边的两个角互为对顶角。
两条直线相交得到的四个角中,有公共顶点,还有一条公共边的两个角互为邻补角。
问题3:邻补角一定互为补角。对顶角又有什么样的大小关系呢?
3
2
1
我们可以做下面的推理:
∵∠1与∠2互补,
∠2与∠3互补(邻补角定义),
∴∠1=∠3(同角的补角相等).
同理,∠2=∠4 .
对顶角相等
D
C
B
A
例题探讨: 如图,射线OC交直线AB于点O,图中共有几个角?它们是邻补角还是对顶角? 为什么?
C
A
B
O
拓展: 邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角。
解:图中共有两个角,它们互为邻补角。因为它们有一个公共边,另一边互为反向延长线。
返回
学生达标一
1、下列各图中,O、P在直线AB上,图中有邻补角吗?有对顶角吗?如果有,请把它们指出来。
无对顶角,有两对邻补角:
∠AOC与∠BOC, ____________
无对顶角,有两对邻补角:
________,∠APD与∠BPD
无对顶角,有三 对邻补角:
__________,∠AOD与∠BOD
∠AOE与∠BOE
无对顶角,有三 对邻补角:
∠AOE与∠BOE, ___________,
∠AOD与∠BOD
A
C
A
B
D
O
(1)
B
C
D
O
P
(2)
C
A
B
D
O
E
(4)
A
B
C
D
O
E
(3)
2、如图,已知直线AE、BD相交于点C.
(1)图中哪些角是对顶角?
A
C
D
E
B
答:邻补角有四对:
∠ACB与∠ACD、∠ACB与∠BCE、
∠DCE与∠ACD、∠DCE与∠BCE.
答:对顶角有两对:
∠ACB与∠DCE、∠ACD与∠BCE.
(2)哪些角是邻补角?
3.如图,AB、CD、EF是经过点O的三条直线,说出:
∠AOC 的对顶角 , ∠FOB 的对顶角 , ∠DOF 的对顶角 , ∠AOD 的对顶角 , ∠EOB 的对顶角 ,∠AOF 的邻补角 、
A
B
C
E
F
D
O
是∠BOD
是∠AOE
是∠COE
是∠BOC
是∠AOF
是∠BOF 和∠AOE
4、下列图形中,∠1和∠2是对顶角的图形是( )
1
1
1
1
2
2
2
2
(A)
(B)
(C)
(D)
C
5、下列说法是否正确?为什么?
(1)有公共顶点的两个角是对顶角。
答:不正确。如图,∠AOB与∠COD有
公共顶点O,但它们不是对顶角。
A
O
C
D
B
(2)有公共顶点而没有公共边的两个角是对顶角。
答:不正确。如上图,∠AOB与∠COD有公共顶点O,而且
没有公共边,但它们不是对顶角。
(3)相邻的两个角是邻补角。
答:不正确。如图,∠AOB 与∠BOC 有
公共顶点和一条公共边,是相邻的两
个角,但不互补,所以不是邻补角。
A
C
B
O
1、 对顶角相等。反过来, 相等的 两个角一定是对顶角吗?
2
3
4
2、邻补角互补。反过来,互补的角(度数的和等于180°的两个角)一定是邻补角吗?
学生达标二
返回
课堂评价与反思:
小结: 今天,我们学习了两直线相交的有关知识,弄清对顶角和邻补角这两个重要概念以及“对顶角相等”这一重要性质,因为它们在我们今后的学习中经常用到;要学会从复杂的图形中分解出基本的图形,从而正确识别对顶角、邻补角,逐步训练和提高自己的识图能力和计算推理能力。
评价:第一组:__分 第二组: __分 第三组: __分
第四组: __分 第五组: __分 第六组: __分
反思:
返回
返回知识链接
返回授课流程
